تحلیل اکتشافی گراف - قسمت اول - پیدا کردن رئوس مشابه

مقدمه

تحلیل اکتشافی یکی از مهم‌ترین قدم‌ها در حل هر مسئله‌ی داده‌کاوی است.
در این مرحله، شما به بررسی الگوهای موجود در داده‌ها می‌پردازید تا درک عمیق‌تری از مسئله پیدا کرده و مسیر درستی برای مراحل بعدی انتخاب کنید.

صورت مسئله

فرض کنید یک گراف ساده و بدون جهت به شما داده شده و تعدادی رأس خاص (دارای رفتاری خاص) در آن مشخص شده‌اند.

سؤال این است:
چطور می‌توان سایر رأس‌هایی که "شبیه" به این رأس‌ها هستند را در گراف پیدا کرد؟

ایده اصلی: کمک گرفتن از Graphletها

یکی از ایده‌های ساده و کاربردی برای تحلیل رفتار رأس‌ها، بررسی Graphletهایی است که آن‌ها در آن‌ها ظاهر می‌شوند.
📌 Graphlet گرافی با n رأس است که غیر هم‌ریخت با دیگر گراف‌های مشابهش با n رأس است. یعنی اگر رئوس بدون نام باشند، نتوانیم با تغییر شکل یا بازچینی به گرافی دیگر برسیم.

مراحل کلی کار:

1. مشخص کردن اینکه رأس‌های خاص، در چه Graphletهایی (و چند بار) ظاهر می‌شوند.

2. بررسی رأس‌های دیگر و مقایسه توزیع Graphletهای آن‌ها با رأس‌های خاص.

3. یافتن شباهت یا تفاوت در این توزیع‌ها.

پیاده‌سازی الگوریتم مرحله به مرحله

گام اول: ساخت Graphletهای تصادفی

برای ساخت نمونه‌هایی از Graphletها:

1. یک رأس تصادفی از میان رأس‌هایی که رفتارشان برای ما مهم است انتخاب می‌کنیم.

2. یکی از همسایه‌های این رأس را برمی‌داریم.

3. سپس یکی از همسایه‌های دو رأس فعلی (اتحادشان) را که هنوز انتخاب نشده‌اند، انتخاب می‌کنیم.

4. این روند را تا حداکثر kk بار ادامه می‌دهیم (اینجا k=6k=6) تا به حداکثر اندازه‌ی Graphlet مورد نظر برسیم.

در نهایت، یک زیرگراف القایی می‌سازیم (یعنی گرافی که فقط شامل رأس‌های انتخاب‌شده و یال‌های بین آن‌هاست).

گام دوم: شمارش و ذخیره Graphletها

• هر Graphlet تولیدشده باید به یک شناسه یکتا تبدیل شود (برای شمارش دقیق).

• برای ذخیره‌سازی، از یک ساختار دیکشنری یا hashmap استفاده می‌کنیم که شمارش تعداد تکرار هر Graphlet را نگه دارد.

• در نهایت، با تقسیم تعداد تکرارها بر تعداد کل نمونه‌ها، توزیع احتمال ظاهر شدن هر Graphlet را محاسبه می‌کنیم.

چالش اصلی: تشخیص گراف‌های هم‌ریخت (isomorphic)

بزرگ‌ترین چالش اینجاست که باید مراقب باشیم گراف‌های هم‌ریخت را دوبار نشماریم!
برای حل این مشکل، دو راهکار داریم:

راهکار اول: استفاده از الگوریتم Havel-Hakimi

در حالتی که محل رأس خاص برای ما اهمیت ندارد (یعنی همه رأس‌ها یکسان فرض می‌شوند)،
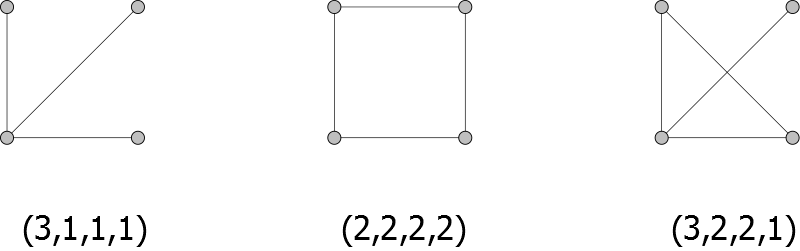
می‌توانیم از بردار درجات مرتب‌شده رأس‌ها به‌عنوان نماینده گراف استفاده کنیم.

• کافی‌ست درجه‌ی هر رأس را بگیریم و به صورت مرتب‌شده کنار هم قرار دهیم.

• این بردار تا حد زیادی یکتا است و می‌توان با الگوریتم Havel-Hakimi گراف متناظر با آن را نیز بازیابی کرد.

⚠️ این روش زمانی مناسب است که نخواهیم رأس خاص را دنبال کنیم. (در بیشتر مواقع این کافی نیست.)

راهکار دوم: استفاده از الگوریتم Color-Refinement

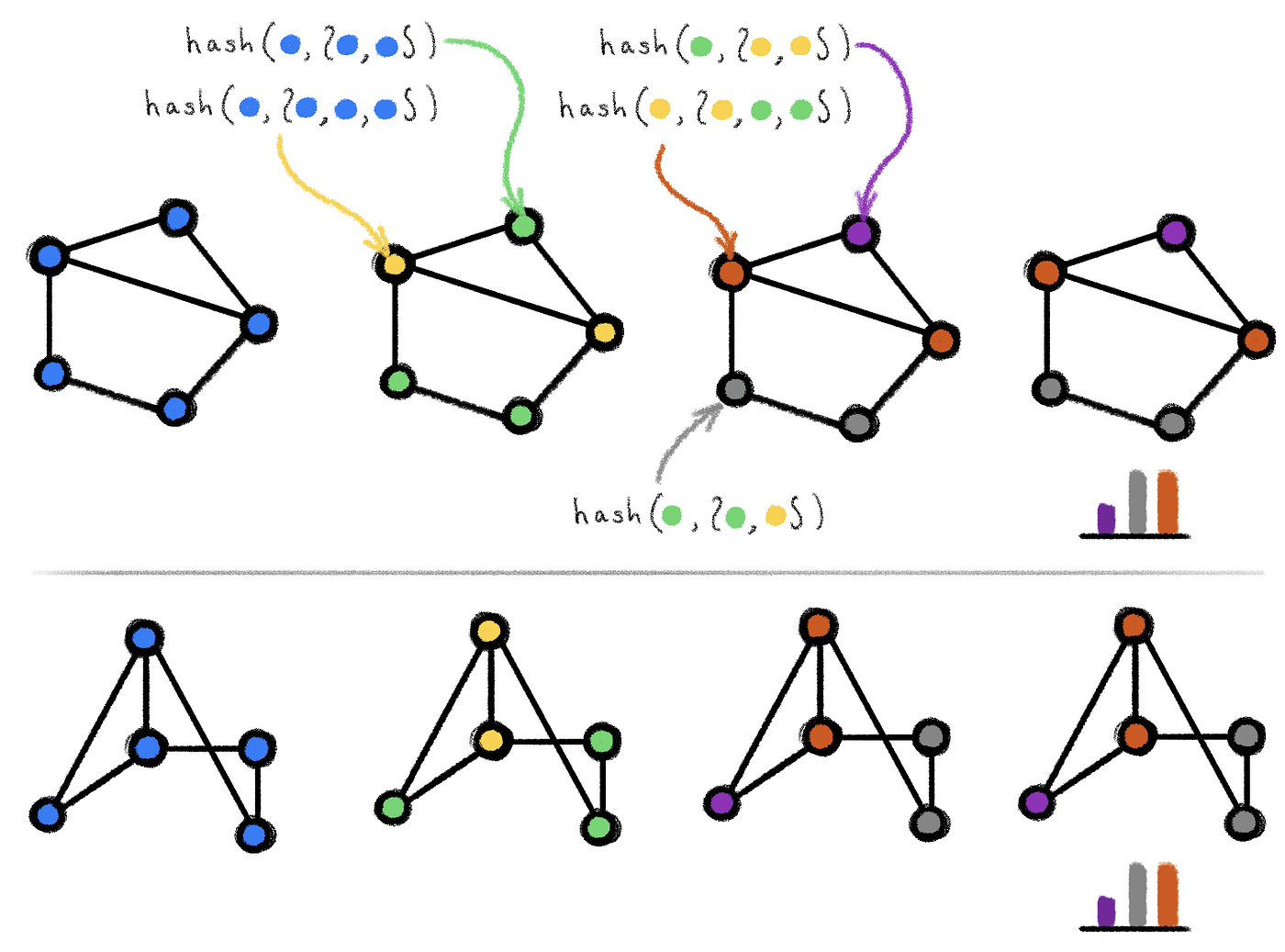
در حالتی که راس خاص اهمیت دارد و می‌خواهیم تقارن بین رأس‌ها را هم بشکنیم، از الگوریتم Color-Refinement استفاده می‌کنیم.

ایده اصلی:

• به هر رأس یک رنگ اولیه نسبت داده می‌شود (مثلاً بر اساس خاص بودن یا نبودن).

• سپس در طی چند مرحله، رنگ‌ها را بر اساس همسایه‌ها به‌روزرسانی می‌کنیم تا به یک امضای یکتا برای گراف برسیم.

الگوریتم Color-Refinement چگونه کار می‌کند؟

1. یک آرایه‌ی seen_colors می‌سازیم و تمام خانه‌هایش را صفر می‌گذاریم.

2. به ازای هر رنگ اولیه، مقدار متناظر در seen_colors را ++ می‌کنیم.

در هر iteration:

الف) برای هر رأس:

• لیستی از رنگ همسایه‌هایش را به‌دست می‌آوریم و صعودی مرتب می‌کنیم.

• عدد رنگ خودش را به ابتدای این لیست اضافه می‌کنیم.

ب) یک تابع رنگ‌ساز (Aggregation Function) روی این لیست اعمال می‌کنیم:

• اگر این لیست قبلاً رنگی داشته، همان رنگ را برمی‌گردانیم.

• در غیر این صورت یک رنگ جدید اختصاص داده و آن را ذخیره می‌کنیم.

ج) برای هر رنگی که در این مرحله استفاده شده، seen_colors[color]++ انجام می‌دهیم.

چند مرحله اجرا کنیم؟

اگر Graphletهایی با اندازه‌ی kk در نظر داریم، کافی‌ست الگوریتم را تا k+1k+1 بار اجرا کنیم.
از این مرحله به بعد، رنگ‌ها همگرا شده‌اند و تغییری نمی‌کنند.

در نهایت، بردار seen_colors به‌عنوان نماینده یکتای گراف استفاده می‌شود.

نویسنده: علی صدفی

ویراستار: ChatGPT