دشواری‌های غلط‌یابی پارسی در قیاس با انگلیسی - ۲

تحلیل تطبیقی غلط‌یابی در زبان‌های پارسی و انگلیسی: از بی‌قاعدگی‌های نوشتاری تا پیچیدگی صرفی (ساختواژه)

بخش اول

۱.۲ فهرست واژگان جایگزین: مدل‌های آماری و احتمالاتی

تهیه فهرستی از گزینه‌های احتمالی تنها نیمی از کار است؛ نرم‌افزار باید این گزینه‌ها را رتبه‌بندی کند تا محتمل‌ترین واژه مورد نظر را به کاربر ارائه دهد. این کار معمولاً با استفاده از مدل‌های احتمالاتی انجام می‌شود که هم احتمال واژه مورد نظر و هم احتمال خطای خاصی که رخ داده است را ارزیابی می‌کنند. یعنی باید احتمال رواج واژه پیشنهادی بررسی شود که واژه پیشنهادی چقدر در زبان رایج است و احتمال خطا، یعنی چقدر محتمل است که کاربر خطایی مرتبط با این واژه را کرده باشد.

یک ابزار و چارچوب کلاسیک و قدرتمند برای این کار مدل کانال نویزدار (Noisy Channel Model) است. این مدل، فرایند نوشتن را به‌عنوان «کانال نویزدار» در نظر می‌گیرد؛ جایی که واژه مورد نظر کاربر (الف) در اثر خطا به واژه مشاهده‌شده و غلط (ب) تبدیل می‌شود. هدف این است که واژه ج پیدا شود که بیشترین احتمال پسینی الف به احتمال ب را دارد.

توضیح کانال نویزدار
در این مدل فرایند نوشتن را مانند یک کانال ارتباطی در نظر می‌گیریم که دارای «نویز» یا «اختلال» است. در این کانال، کلمه‌ی صحیح و اصلی که کاربر قصد داشته تایپ کند (w)، به دلیل خطاهای تایپی (نویز) خراب شده و به شکل یک کلمه‌ی غلط (x) درآمده است.

• کلمه‌ی اصلی (w): کلمه‌ای که کاربر قصد تایپ آن را داشته (مثلاً: «کتاب»).

• کلمه‌ی مشاهده‌شده (x): کلمه‌ی غلطی که در عمل تایپ شده (مثلاً: «کناب»).

• هدف نهایی: پیدا کردن محتمل‌ترین کلمه‌ی اصلی (w)، با توجه به کلمه‌ی غلطی (x) که مشاهده کرده‌ایم.

استفاده از قضیه بیز Bayes

این مدل تلاش می‌کند تا بهترین گزینه جایگزین (w^) را با بیشینه کردن احتمال P(w∣x) پیدا کند. این عبارت یعنی: «احتمال اینکه کلمه‌ی اصلی w بوده باشد، به شرط اینکه ما کلمه‌ی غلط x را دیده‌ایم.»

با استفاده از قضیه بیز، این رابطه به شکل زیر بازنویسی می‌شود:

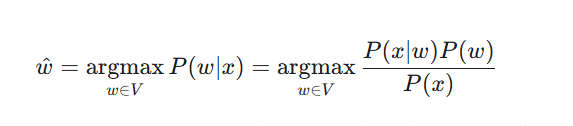
از آنجایی که P(x) (احتمال مشاهده‌ی خودِ کلمه‌ی غلط) برای تمام کلمات نامزد یکسان است و در انتخاب بهترین کلمه تأثیری ندارد، می‌توانیم آن را نادیده بگیریم. در نتیجه، مسئله به پیدا کردن بیشترین مقدار برای عبارت زیر ساده می‌شود:

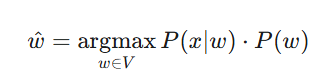
این فرمول نهایی از دو بخش کلیدی تشکیل شده است:

• P(w) - مدل زبانی (Language Model): این بخش، احتمال وقوع خود کلمه‌ی w در زبان را نشان می‌دهد. به عبارت دیگر، این مدل به این سؤال پاسخ می‌دهد: «این کلمه چقدر رایج و محتمل است؟» برای مثال، احتمال کلمه‌ی «برای» بسیار بیشتر از «باری» است. این بخش باعث می‌شود سیستم کلمات رایج و معنادار را ترجیح دهد.

• P(x∣w) - مدل خطا (Error Model): این بخش، احتمال تایپ شدن کلمه‌ی غلط x به شرطی که کلمه‌ی اصلی w بوده باشد را محاسبه می‌کند. این مدل به این سؤال پاسخ می‌دهد: «این نوع غلط تایپی چقدر محتمل است؟».

  این مدل، احتمال خطاهای رایج تایپی را محاسبه می‌کند، مانند:

  جایگزینی: تایپ «کناب» به جای «کتاب» (چون 'ن' و 'ت' روی کیبورد نزدیک هم هستند، احتمال این خطا بالاست).

  جابجایی: تایپ «کاتب» به جای «کتاب».
  حذف: تایپ «کتب» به جای «کتاب».
  درج: تایپ «کتااب» به جای «کتاب».

به طور خلاصه، مدل کانال نویزدار بهترین اصلاح را برای یک کلمه‌ی غلط پیدا می‌کند. این اصلاح، کلمه‌ای است که بهترین توازن را بین دو معیار برقرار کند: اول اینکه کلمه‌ای رایج در زبان باشد (بر اساس مدل زبانی) و دوم اینکه توضیح خوبی برای نوع غلط نوشتاری مشاهده‌شده ارائه دهد (بر اساس مدل خطا).

شاید بهتر باشد، قبل از پیش‌رفتن در موضوع توضیحی درباره قضیه بیز یا Bayes' theorem داده شود.

قضیه بیز: به‌روزرسانی باور با شواهد جدید

۲ نوع نگاه به پدیده احتمال وجود دارد. در نگاه کلاسیک یا نگاه فرکانسی یا بسامدی، احتمال یک رویداد، همان فرکانس یا تکرار وقوع آن در بلندمدت است. مثلاً احتمال آمدن «شیر» در پرتاب سکه ½ است، چون اگر هزاران بار سکه را پرتاب کنیم، انتظار داریم تقریباً نیمی از نتایج «شیر» باشد. این دیدگاه برای رویدادهای غیرقابل تکرار (مانند احتمال قهرمانی یک تیم خاص در جام جهانی بعدی) معنای روشنی ندارد.

نگاه بیزی (Bayesian): در این دیدگاه، احتمال یک معیار برای سنجش میزان اطمینان یا باور به یک گزاره است. این باور می‌تواند بر اساس دانش قبلی، تجربیات شخصی یا شهود باشد و با رسیدن اطلاعات و شواهد جدید، دائماً به‌روز می‌شود. به عبارت دیگر، در تفکر بیزی، احتمالات به جای اینکه ویژگی ثابتی از دنیای بیرون باشند، نمایانگر میزان دانش و اطمینان ما درباره آن هستند. این دیدگاه به ما اجازه می‌دهد برای هر چیزی، از نتایج آزمایش‌های علمی گرفته تا اتفاقات روزمره، یک درجه از باور تعریف کرده و آن را با منطق ریاضی اصلاح و به‌روز کنیم. این همان کاری است که ذهن ما به طور ناخودآگاه در تصمیم‌گیری‌های روزانه انجام می‌دهد.

قضیه بیز به طور خلاصه می‌گوید چگونه می‌توانیم احتمال یک فرضیه (A) را پس از مشاهده یک شاهد (B) محاسبه کنیم. این قضیه به ما کمک می‌کند تا از دانش و باور اولیه خود شروع کرده و با رسیدن اطلاعات جدید، آن را اصلاح کنیم.
اگر P(A∣B) (احتمال یا باور پسین یا بعدی یا جدید - Posterior): احتمال یا باور به درست بودن فرضیه A بعد از مشاهده شاهد B باشد، به این صورت دانش یا باور قبلی ما به‌روز می‌شود:

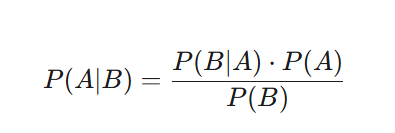
اجزای این فرمول عبارتند از:

• P(A∣B) (احتمال پسین - Posterior): احتمال درست بودن فرضیه A بعد از مشاهده شاهد B. این همان باور به‌روز شده‌ی ماست.

• P(B∣A) (احتمال شرطی - Likelihood): احتمال مشاهده شاهد B، به شرط اینکه فرضیه A درست باشد.

• P(A) (احتمال پیشین - Prior): باور اولیه‌ی ما به درستی فرضیه A قبل از مشاهده هرگونه شاهد جدید.

• P(B) (احتمال شاهد - Evidence): احتمال کلی مشاهده شاهد B.

مثال: تست یک بیماری نادر

فرض کنید بیماری نادری وجود دارد که ۱ نفر از هر ۱۰۰۰ نفر (یعنی ۰.۱٪) در جامعه به آن مبتلا است. آزمایش تشخیصی بسیار خوبی برای این بیماری داریم که ویژگی‌های زیر را دارد:

• دقت تست در افراد بیمار (حساسیت - Sensitivity): اگر فردی واقعاً بیمار باشد، تست به احتمال ۹۹٪ به درستی مثبت می‌شود.

• دقت تست در افراد سالم (ویژه‌ بودن - Specificity): اگر فردی سالم باشد، تست به احتمال ۹۸٪ به درستی منفی می‌شود (یعنی ۲٪ خطا در افراد سالم دارد و نتیجه را به اشتباه مثبت نشان می‌دهد).

حالا، شما به صورت تصادفی آزمایش می‌دهید و نتیجه آزمایش‌تان مثبت می‌شود. سوال این است:

چقدر احتمال دارد که واقعاً به این بیماری مبتلا باشید؟

تحلیل با استفاده از قضیه بیز

بیایید اجزای مسئله را در فرمول بیز قرار دهیم:

• P(A) (احتمال پیشین): احتمال بیمار بودن قبل از انجام آزمایش. این همان شیوع بیماری در جامعه است.

  P(بیمار بودن)=0.001 (یک در هزار)

• P(B∣A) (احتمال شرطی): احتمال مثبت شدن آزمایش، به شرطی که واقعاً بیمار باشید. این همان حساسیت آزمایش است.

  P(تست مثبت∣بیمار بودن)=0.99

• P(B) (احتمال کلی تست مثبت): این بخش کمی پیچیده‌تر است. یک تست مثبت می‌تواند به دو دلیل رخ دهد:

  شما بیمار هستید و تست به درستی مثبت شده.
  شما سالم هستید و تست به اشتباه مثبت شده (مثبت کاذب).

• احتمال حالت اول: P(بیمار بودن)×P(تست مثبت∣بیمار بودن)=0.001×0.99=0.00099

• احتمال حالت دوم: P(سالم بودن)×P(تست مثبت∣سالم بودن)=0.999×0.02=0.01998

• P(تست مثبت) (مجموع دو حالت): 0.00099+0.01998=0.02097

حالا محاسبه نهایی

با جای‌گذاری اعداد

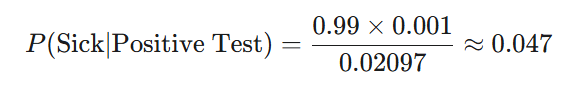
بر خلاف ذهنیت اولیه ما، در صورت مثبث بودن تست، تنها ۴.۷ درصد احتمال دارد که بیمار باشید. با وجود اینکه تست ۹۹٪ دقیق است، مثبت بودن نتیجه آزمایش به این معناست که هنوز هم بیش از ۹۵٪ احتمال دارد سالم باشید. اما چرا؟

دلیل اصلی، نادر بودن بیماری است. چون بیماری بسیار کمیاب است، تعداد افراد سالمی که تستشان به اشتباه مثبت می‌شود (مثبت کاذب)، بسیار بیشتر از تعداد افراد بیماری است که تستشان به درستی مثبت شده است.
چرا این عدد در ابتدا دور از ذهن می‌آید؟
فرض کنید که در شهری ۱۰،۰۰۰ نفری زندگی می‌کنید. در شهر تنها ۱ دهم درصد یا ۱ نفر از ۱۰۰۰ نفر بیمار هستند. یعنی تنها ۱۰ نفر در کل شهر بیمار هستند و ۹۹۹۰ نفر سالم هستند.
وقتی هر ۱۰ نفر بیمار آزمایش بدهند به دلیل دقت ۹۹ درصدی تست، جواب آزمایش ۹/۹ نفر یا همه ۱۰ نفر مثبت می‌شود.
اما به دلیل خطای ۲ درصدی، اگر ۹۹۹۰ نفر باقی مانده آزمایش بدهند ۱۹۹/۸ نفر یا ۲۰۰ نفر به اشتباه جواب مثبت از آزمایش می‌گیرند.
در مجموع جواب آزمایش ۱۰ نفر بیمار و ۲۰۰ فرد سالم یعنی ۲۱۰ نفر از کل جمعیت شهر ۱۰ هزار نفری مثبت خواهد شد. از این ۲۱۰ نفر تنها ۱۰ نفر واقعا بیمار هستند، پس احتمال بیماری ۱۰ از ۲۱۰ یا همان ۴.۷ درصد است.
این مثال به خوبی نشان می‌دهد که چطور باور اولیه ما (کمیاب بودن بیماری) تأثیر عظیمی بر تفسیر شواهد جدید (نتیجه تست مثبت) دارد.

بخش ۳