LeetCode75
238. Product of Array Except Self
Given an integer array nums, return an array answer such that answer[i] is equal to the product of all the elements of nums except nums[i].
The product of any prefix or suffix of nums is guaranteed to fit in a 32-bit integer.
You must write an algorithm that runs in O(n) time and without using the division operation.
Example 1:
Input: nums = [1,2,3,4] Output: [24,12,8,6]
Example 2:
Input: nums = [-1,1,0,-3,3] Output: [0,0,9,0,0]
Constraints:
2 <= nums.length <= 105-30 <= nums[i] <= 30answer[i] is guaranteed to fit in a 32-bit integer.O(n) بدون تقسیم)این سؤال میخواهد که برای هر عنصر آرایه، حاصلضرب تمام عناصر دیگر محاسبه شود، اما بدون استفاده از عمل تقسیم.
ما باید راهی پیدا کنیم که در زمان O(n) حل شود.
prefix و suffix)✅ ایدهی کلی این است که برای هر عنصر nums[i]:
prefix product)suffix product)بدون نیاز به O(n²) یا تقسیم، این کار را در O(n) انجام میدهیم.
📌 کد O(n) بدون تقسیم:
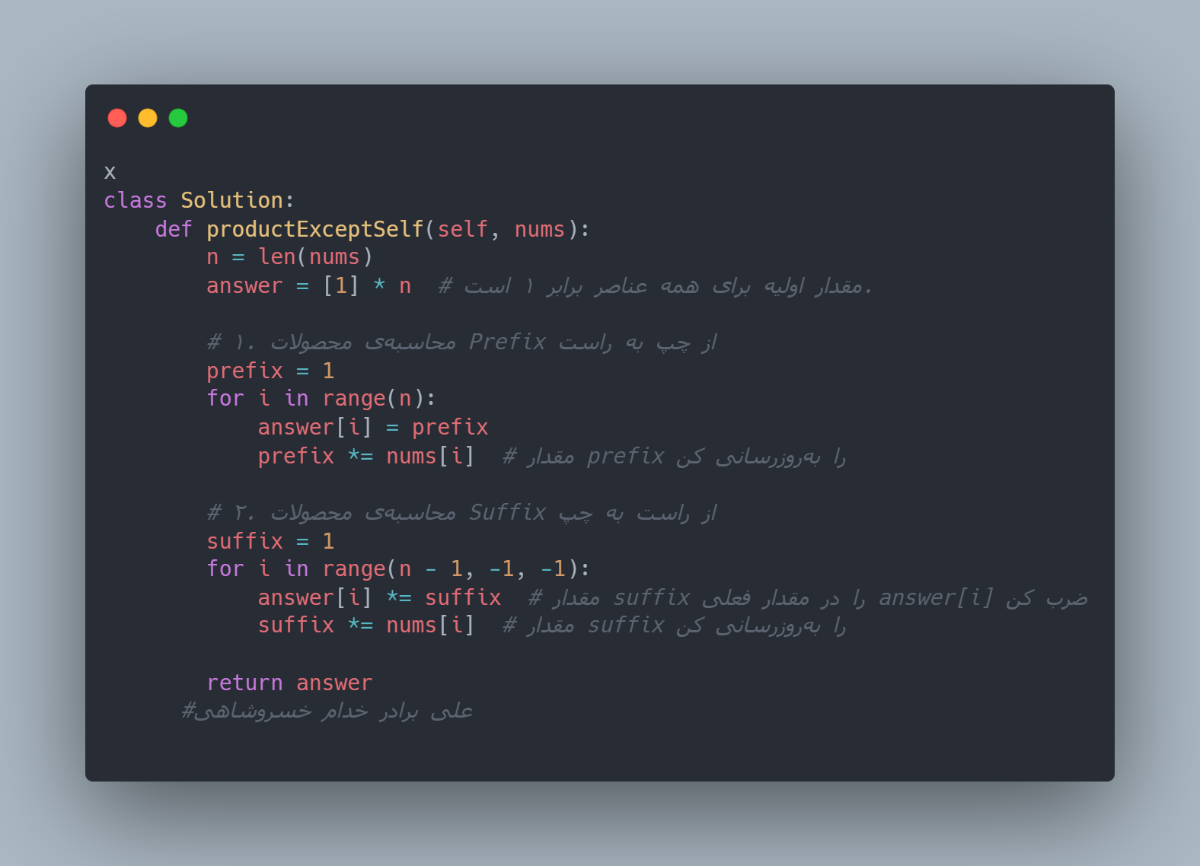
class Solution:
def productExceptSelf(self, nums):
n = len(nums)
# مقدار اولیه برای همه عناصر برابر ۱ است.
answer = [1] * n
# ۱. محاسبهی محصولات Prefix از چپ به راست
prefix = 1
for i in range(n):
answer[i] = prefix
# مقدار prefix را بهروزرسانی کن
prefix *= nums[i]
# ۲. محاسبهی محصولات Suffix از راست به چپ
suffix = 1
for i in range(n - 1, -1, -1):
# مقدار suffix را در مقدار فعلی answer[i] ضرب کن
answer[i] *= suffix
# مقدار suffix را بهروزرسانی کن
suffix *= nums[i]
return answer
# علی برادر خدام خسروشاهی
📌 توضیح مرحلهبهمرحله
✅ ۱. محاسبهی prefix (محصول عناصر قبل از nums[i])
prefix ابتدا ۱ است.prefix در nums[i] ضرب شده و در prefix بعدی ذخیره میشود.✅ ۲. محاسبهی suffix (محصول عناصر بعد از nums[i])
suffix ابتدا ۱ است.answer[i] در مقدار suffix ضرب شده و suffix بهروزرسانی میشود.✅ پیچیدگی زمانی: O(n) (دو بار عبور از آرایه)
✅ پیچیدگی فضایی: O(1) (چون فقط از متغیرهای prefix و suffix استفاده کردیم و answer را از قبل داشتیم)
O(n²) محاسبهی ضرب ندارد./) ندارد که در برخی موارد مشکل ایجاد میکند.O(n) برای این مسئله است. 🚀علی برادر خدام خسروشاهی