الگوریتم تبرید شبیه سازی شده (Simulated Annealing)

الگوریتم تبرید شبیه سازی شده (Simulated Annealing) یه الگوریتم بهینه‌سازی از نوع قطعیه (تو پست های قبلی هم به این نوع الگوریتم‌ها اشاره کردم ولی این توضیح رو داشته باشید: الگوریتم‌های بهینه‌سازی قطعی مثل اون دوستای منظمی هستن که همه‌چیز رو طبق برنامه و بدون هیچ شانسی انجام می‌دن. این الگوریتم‌ها به نوعی دقیق و منطقی پیش میرن و معمولاً از فرمول‌های ریاضی برای پیدا کردن بهترین راه‌حل استفاده می‌کنن.)

حالا الگوریتم تبرید شبیه سازی شده دقیقا چیه؟
تصور کن که در حال بازدید از یک شهر قدیمی پر از تپه و دره هستی و می‌خوای به بالاترین تپه برسی. اما اگه فقط به سمت بالا حرکت کنی، ممکنه در تپه‌های کوچکتر گیر بیفتی و نتونی به بلندترین تپه برسی. الگوریتم تبرید شبیه‌سازی شده مثل یه نقشه هست که بهت کمک می‌کنه حتی اگه بعضی وقتا به سمت پایین حرکت کنی، در نهایت به بلندترین تپه برسی.

چطوری کار می‌کنه؟
این الگوریتم از مفهوم تبرید در فیزیک الهام گرفته که در اون یک ماده ابتدا گرم و سپس به تدریج سرد می‌شه. همونطور که دمای سیستم کاهش پیدا می‌کنه، حرکت ذرات هم کم کم آروم می‌شه و سیستم به حالت پایدار (یا بهینه) خودش می‌رسه.

۱. شروع با یک دما و راه‌حل اولیه: دما رو روی مقدار بالایی تنظیم می‌کنی و با یه راه‌حل اولیه شروع می‌کنی.
۲. پیدا کردن همسایه‌های راه‌حل فعلی: در هر مرحله، همسایه‌هایی برای راه‌حل فعلی پیدا می‌کنی (مثلاً با تغییرات کوچیک).
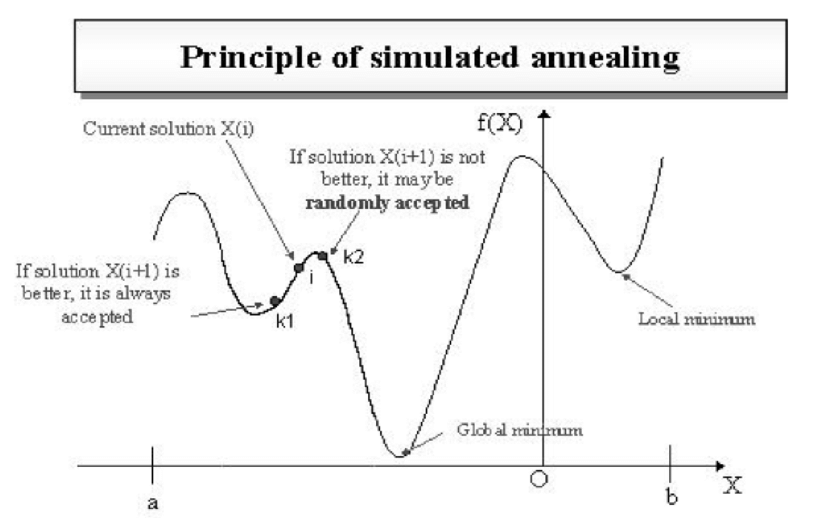
۳. قبول یا رد راه‌حل جدید: اگه راه‌حل جدید بهتر باشه، اون رو قبول می‌کنی. اما اگه بدتر باشه، با احتمالی که به دما وابسته‌ است، ممکنه اون رو قبول کنی. به این میگن "پذیرش توسط جهش".
۴. کاهش دما: دما رو به تدریج کم می‌کنی و این مراحل رو تکرار می‌کنی تا دما خیلی کم بشه و به یک راه‌حل نهایی برسی.

مثلا برای این‌که راحت‌تر بفهمی: فرض کن تو یه فروشگاه زنجیره‌ای کار می‌کنی و باید چیدمان قفسه‌ها رو بهینه کنی تا فروش بیشتری داشته باشی. با استفاده از الگوریتم تبرید شبیه‌سازی شده، می‌تونی چیدمان‌های مختلف رو امتحان کنی و حتی اگر یک چیدمان کمتر خوب به نظر برسه، ممکنه در طول زمان به یک چیدمان بهتر منجر بشه.

مزایا

- ساده و انعطاف‌پذیر: به راحتی می‌تونه برای مسائل مختلف تنظیم بشه.
- پرهیز از افتادن در کمینه‌های محلی: به دلیل پذیرش راه‌حل‌های بدتر در ابتدا، به بهینه سراسری نزدیک می‌شه.

معایب

- زمان‌بر: به خاطر نیاز به تنظیم دما و تعداد زیادی تکرارها، ممکنه زمان زیادی ببره.
- نیاز به تنظیمات دقیق: پارامترهایی مثل نرخ کاهش دما باید به دقت تنظیم بشن تا الگوریتم بهینه عمل کنه.

این مثال یک مسئله ساده رو حل می‌کنه: پیدا کردن کمینه یک تابع یک‌بعدی به نام f(x) = x^2 + 4*sin(5*x) + 3*cos(3*x) در بازه [−10, 10].

#include <iostream>
#include <cmath>
#include <cstdlib>
#include <ctime>

double f(double x) {
    return x * x + 4 * sin(5 * x) + 3 * cos(3 * x);
}

double getRandom(double min, double max) {
    return min + (double)rand() / RAND_MAX * (max - min);
}

double simulatedAnnealing(double initialTemp, double coolingRate, double minTemp) {
    double x = getRandom(-10, 10);  // شروع با یک راه‌حل تصادفی
    double temp = initialTemp;

    while (temp > minTemp) {
        double newX = x + getRandom(-1, 1);  // تولید یک راه‌حل همسایه
        newX = std::min(10.0, std::max(-10.0, newX));  // محدود کردن به بازه [−10, 10]

        double deltaE = f(newX) - f(x);

        if (deltaE < 0 || exp(-deltaE / temp) > getRandom(0, 1)) {
            x = newX;  // پذیرش راه‌حل جدید
        }

        temp *= coolingRate;  // کاهش دما
    }

    return x;
}

int main() {
    srand(time(0));  // مقداردهی تصادفی

    double initialTemp = 1000;
    double coolingRate = 0.99;
    double minTemp = 0.01;

    double result = simulatedAnnealing(initialTemp, coolingRate, minTemp);
    std::cout << &quotMinimum found at x = &quot << result << &quot, f(x) = &quot << f(result) << std::endl;

    return 0;
}

توضیحات کد:

۱. تابع f:تابع هدف که می‌خوایم کمینه اون رو پیدا کنیم.

۲. تابع getRandom: برای تولید اعداد تصادفی در یک بازه مشخص.

۳.تابع simulatedAnnealing: پیاده‌سازی الگوریتم تبرید شبیه سازی شده.

۴.حلقه‌ی اصلی: در هر مرحله، دما کاهش پیدا می‌کنه و یک راه حل همسایه جدید ایجاد میشه. اگه راه حل جدید بهتر باشه با یک احتمال مشخص، اون رو قبول می‌کنیم.

۵. مقداردهی اولیه: تنظیمات دمای اولیه، نرخ کاهش دما و دمای کمینه.

امیدوارم این مطلب براتون مفید بوده باشه و مثل همیشه اگه می‌خواید بیشتر با این موضوع آشنا بشید منابع بیشتری رو مطالعه کنید✨️.