الگوریتم هافمن (Huffman Coding) یه الگوریتم از نوع حریصانه برای فشرده سازی دادههاست
حالا الگوریتمهای حریصانه در کل چی هستن؟ الگوریتم حریصانه (Greedy) در هر مرحله از حل مسئله، بهترین انتخاب ممکن در همان لحظه رو انجام میده، بدون اینکه به پیامدهای آینده یا انتخابهای قبلی توجه کنه. یعنی مثل کسی که تو فروشگاه دنبال خرید با کمترین پول باشه و فقط به قیمت لحظهای نگاه کنه، نه اینکه کل سبد خرید رو بررسی کنه.
ویژگیهاش:
- تصمیمگیری مرحلهای: در هر گام، بهترین گزینه انتخاب میشه.
- عدم بازگشت: انتخابها نهایی هستن و به عقب برنمیگرده.
- سادگی و سرعت بالا: چون نیازی به بررسی همه حالتها نداره.
- جواب تقریبی یا بهینه: گاهی جواب کاملاً بهینه میده، گاهی فقط نزدیک به بهینه.
حالا نکته اینجاست، برای اینکه این الگوریتم جواب درست بده، مسئله باید دو ویژگی داشته باشه:
اولا خاصیت انتخاب حریصانه (Greedy Choice Property): انتخاب بهترین گزینه در هر مرحله باید منجر به بهترین جواب کلی بشه.
دوما زیرساختار بهینه (Optimal Substructure): مسئله باید قابل تقسیم به زیرمسئلههایی باشه که خودشون هم قابل حل با همین روش باشن.
حالا الگوریتم هافمن (Huffman) چیه؟
الگوریتم هافمن که برای فشردهسازی دادهها استفاده میشه ایدهاش اینه:
یک، کاراکترهایی که بیشتر تکرار میشن، با کدهای کوتاهتر نمایش داده بشن
و دو، کاراکترهای کمتکرار، با کدهای بلندتر
این باعث میشه حجم داده نهایی کمتر بشه و انتقال یا ذخیرهسازی سریعتر انجام بشه.
مراحل اجرا:
۱. محاسبه فراوانی کاراکترها
مثلاً در رشتهی "asmaaa"، کاراکتر a سه بار، s و m هرکدوم یک بار ظاهر شدن.
۲. ساخت درخت هافمن
- هر کاراکتر بهعنوان یک گره با وزن (فراوانی) در نظر گرفته میشه.
- دو گره با کمترین وزن با هم ترکیب میشن.
- این کار ادامه پیدا میکنه تا فقط یک درخت باقی بمونه.
۳. تخصیص کد دودویی به هر کاراکتر
- حرکت به چپ: 0
- حرکت به راست: 1
- مسیر هر کاراکتر از ریشه تا برگ، کد اون کاراکتره.
اگه بخوایم یه مثال بزنیم
فرض کن رشتهای داریم با کاراکترهای زیر و فراوانیهاشون:
| کاراکتر | فراوانی |
| A | 5 |
| B | 9 |
| C | 12 |
| D | 13 |
| E | 16 |
| F | 45 |
بعد از ساخت درخت هافمن، ممکنه کدها به شکل زیر باشن:
| کاراکتر | کد هافمن |
| F | 0 |
| C | 100 |
| D | 101 |
| A | 1100 |
| B | 1101 |
| E | 111 |
میبینی که کاراکتر F که بیشترین فراوانی رو داره، کوتاهترین کد رو گرفته
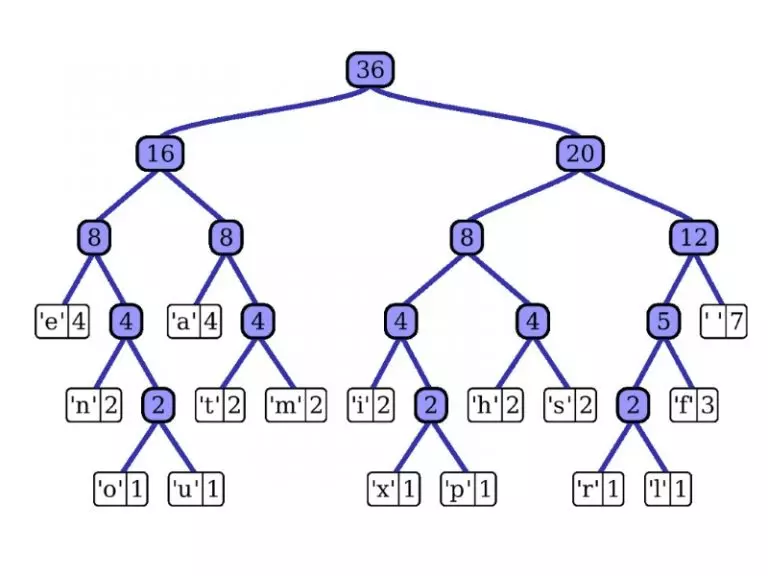
حالا برای درک بهترش میشه یه مسئله حل کرد
cpp
include <iostream>
include <queue>
include <unordered_map>
using namespace std;
struct Node {
char ch;
int freq;
Node left, right;
Node(char c, int f) {
ch = c;
freq = f;
left = right = nullptr;
}
};
struct Compare {
bool operator()(Node a, Node b) {
return a->freq > b->freq;
}
};
Node* buildHuffmanTree(unordered_map<char, int> freqMap) {
priority_queue<Node, vector<Node>, Compare> pq;
for (auto pair : freqMap) {
pq.push(new Node(pair.first, pair.second));
}
while (pq.size() > 1) {
Node* left = pq.top(); pq.pop();
Node* right = pq.top(); pq.pop();
Node* merged = new Node('\0', left->freq + right->freq);
merged->left = left;
merged->right = right;
pq.push(merged);
}
return pq.top();
}
void generateCodes(Node* root, string code, unordered_map<char, string>& huffmanCode) {
if (!root) return;
if (root->ch != '\0') {
huffmanCode[root->ch] = code;
}
generateCodes(root->left, code + "0", huffmanCode);
generateCodes(root->right, code + "1", huffmanCode);
}
توضیح :
۱. ساختار Node
هر گره شامل یک کاراکتر، فرکانس، و اشارهگر به فرزندان چپ و راست هست.
۲. صف اولویتدار (Priority Queue)
گرهها بر اساس فرکانس مرتب میشن. کمترین فرکانس اولویت بیشتری داره.
۳. ساخت درخت هافمن
- دو گره با کمترین فرکانس انتخاب میشن.
- با هم ترکیب میشن و گره جدیدی ساخته میشه.
- این گره جدید دوباره وارد صف میشه.
- این روند ادامه پیدا میکنه تا فقط یک گره باقی بمونه → ریشه درخت.
۴. تولید کدهای دودویی
با پیمایش درخت از ریشه تا برگها:
- حرکت به چپ → اضافه کردن 0
- حرکت به راست → اضافه کردن 1
- مسیر هر برگ (کاراکتر) تبدیل به کد هافمن اون کاراکتر میشه.
امیدوارم این مطلب براتون مفید بوده باشه...