کتاب معماری کامپیوتر موریس مانو
تعداد صفحات:678
نویسنده:موریس مانو
مترجم:مریم شکری حیاثوندی
بخشی از متن کتاب:
دیاگرام منطقی تمام جمع کننده در شکل ۱۸-۱ رسم شده است. توجه کنید که میدار تمام جمع کننده از دو نیم جمع کننده و یک گیت OR ساخته شده است. هنگام استفاده از یک تمام جمع کننده (FA)، شکل ۱۸-۱ (ب) بکار گرفته خواهد شد.
6-1 فلیپ فلاپها[1]
تا کنون مدارهای بررسی شده دیجیتال از نوع ترکیبی بودند، که در آنها خروجی ها در هر لحظه کلا به ورودی های همان لحظه بستگی داشتند. هرچند هر سیستم دیجیتال احتمالا یک مدار ترکیبی دارد، اغلب سیستم هایی که در عمل با آنها مواجه می شویم دارای عناصر حافظه نیز هستند و لذا سیستم باید در چهارچوب مدارهای ترتیبی مورد بررسی قرار گیرد. متداول ترین نوع مدار ترتیبی نوع همگام[2] (همزمان یا سنکرون) آن است. مدارهای ترتیبی همگام در لحظه های گسسته و معینی از زمان بر عناصر حافظه اثر می گذارند. همزمان سازی با یک وسیله زمانبندی یا یک مولد پالس ساعت[3] حاصل می شود که رشته ای از پالس های ساعت را بطور پریودیک تولید می نماید. پالس های دانلود کتاب معماری کامپیوتر موریس مانو در سراسر سیستم توزیع می شوند و عناصر حافظه فقط با رسیدن پالس همگام کننده تأثیر می پذیرند. مدارهای همگام ساعت دار مدارهایی هستند که بیش از همه در عمل با آنها مواجه می شویم. این مدار هيا ندرتا با مسئله ناپایداری روبرو هستند و زمانبندی آنها به مقاطع زمانی مستقل قابل تفکیک می باشند. هر یک از این مقاطع بطور جداگانه قابل بررسی می باشند.
عناصر حافظه بکار رفته در مدار های ترتیبی ساعت دار فلیپ فلاپ خوانده می شوند. فلیپ فلاپ یک سلول[4]دودویی است که می تواند یک بیت اطلاعات را در خود ذخیره نماید. این سلول دارای دو خروجی است، یکی برای مقدار عادی بیتی که در آن ذخیره می شود و دیگری مقدار متمم آن. فلیپ فلاپ یک وضعیت[5] دودویی را در خود نگه میدارد تا اینکه یک پالس ساعت موجب تغییر آن حالت شود. تفاوت بین انواع فلیپ فلاپها در تعداد ورودی های آنها و نحوه تأثیر این ورودی ها بر وضعیت با حالت دودویی آنهاست، متداول ترین انواع فلیپ فلاپها در بخش های زیر ارائه شده اند.
فلیپ فلاپ SR
سمبل گرافیکی فلیپ فلاپ SR در شکل ۱۹-۱ (الف) دیده می شود. این فلیپ فلاپ دارای سه ورودی با نام های نشاندن[6] (S) حذف کردن[7] (R) و ساعت[8] (C) است. خروجی فلیپ فلاپ Q نامیده می شود و گاهی دارای خروجی متمم شده نیز هست که با دایره کوچکی در پایانه خروجی دیگر مشخص شده است. در جلو حرف C یک نوک فلش قرار گرفته که بمعنی دینامیک بودن (پویا بودن) ورودی است. سمبل دینامیکی نشاندهنده این واقعیت است که فلیپ فلاپ به گذار مثبت (لبه بالا رونده) پالس پاسخ می دهد

عملکرد فلیپ فلاپ SR يشرح زیر است. اگر سیگنالی در ورودی ساعت C وجود نداشته باشد مقادیر در ورودی های Sو R هرچه باشند، خروجی مدار تغییری نمی یابد. فقط وقتی که سیگنال ساعت از لایه 1 تغییر نماید خروجی تحت تأثیر ورودی های S و R قرار خواهد گرفت. بهنگام تغییر C از 0 به 1 اگر S=1 و R=0 باشند در خروجی Q مقدار 1 نشانده می شود. اگر در تغییر C از 0 به 1 مقادیر S=0 و R=1 باشند خروجی Q با 0 پاک می شود. اگر در گذار ساعت (از 0 به 1)، S و R هر دو 0 باشند خروجی تغییری نمی کند. هنگامی که S و R هر دو 1 باشند،خروجی غیر قابل پیش بینی است و به تاخیرهای داخلی که در مدار رخ می دهد بستگی داشته و ممکن است 0 و یا 1 گردد.
جدول مشخصه شکل ۱۹-1(ب) عملکرد یک فلیپ فلاپ SR را جدول وار نشان می دهد. در ستون های S و R مقادیر دودویی در ورودی مشخص شده اند. Q (t) نیز حالت خروجی Q در یک زمان معین است (که به آن حالت فعلی می گویند). حالت دودویی خروجی Q پس از لبه مثبت پالس ساعت است (حالت بعدی). اگر S=R=0 باشد،لبه (گذار) پالس تغییری در حالت بوجود نمی آورد [یعنی ].اگر S=0 و R=1باشد فلیپ فلاپ به وضعیت 0 (پاک شده) می رود. اگر S=1 و R=0باشد فیلیپ فلاپ به وضعیت 1 (نشانده شده ) می رود. به فلیپ فلاپ در S=1 و R=0 نباید پالس داد زیرا تولید حالت بعدی نامعینی را خواهد کرد. این حالت نامعین کنترل فلیپ فلاپ را مشخص می سازد و لذا در عمل بندرت مورد استفاده قرار می گیرد.
فلیپ فلاپ D [9]
فلیپ فلاپ D (داده) با تغییر دانلود کتاب معماری کامپیوتر موریس مانو در فلیپ فلاپ SR بدست می آید. فلیپ فلاپ SR با قرار دادن یک معکوس کننده بین Sو R و اختصاص سمبل D به تنها ورودی حاصل، به فلیپ فلاپ D تبدیل می شود. ورودی D هنگام انتقال پالس ساعت از 0 به 1 نمونه برداری می شود. اگر D=1 باشد، خروجی فلیپ فلاپ به حالت 1 می رود، اما در D=0، خروجی فلیپ فلاپ به وضعیت 0 خواهد رفت.
این بدان معنی است که خروجی Q فلیپ فلاپ مقدار خود را،هر بار بهنگام انتقال سیگنال ساعت از 0 به 1 از ورودی D دریافت می کند.
دقت کنید که حالتی از فلیپ فلاپ وجود ندارد که خروجی را تغییر ندهد.هر چند فلیپ فلاپ D از مزیت داشتن فقط یک ورودی (بدون احتساب C) بهره می برد.ولی عیب آن این است که جدول مشخصه آن فاقد حالت بلاتغییر[10] می باشد.در این فلیپ فلاپ حالت بلاتغییر بدین صورت انجام می شود که یا باید سیگنال ساعت غیر فعال گردد و یا خروجی فلیپ فلاپ به ورودی آن بازگردانده[11] شود، بطوری که پالس های ساعت حالت فلیپ فلاپ را تغییر ندهند.
فلیپ فلاپ JK
یک فلیپ فلاپ JK نوع اصلاح شده قلیپ فلاپ SR است که حالت نامعین[12]در فیلپ فلاپ SR در آن معین شده است. ورودی های J و K در نشاندن و یا پاک کردن فلیپ فلاپ بترتيب مانند S و R عمل می کنند. وقتی هر دو ورودی J و K برابر 1 باشند، انتقال یا گذار پالس ساعت خروجی های فلیپ فلاپ را به حالت متممشان سوئیچ می کنند.

(الف) سمبل گرافیکی
(ب) جدول مشخصه
شکل 21-1 فلیپ فلاپ JK
نوع دیگری از فلیپ فلاپها که در کتب درسی دیده می شود فلیپ فلاپ T می باشد. این فلیپ فلاپ، که در شکل ۲۲-۱ نشان داده شده است از فلیپ فلاپ نوع JK و با اتصال ورودی های J و K به یکدیگر و در نتیجه ایجاد یک ورودی واحد که با T نشان داده می دانلود کتاب معماری کامپیوتر موریس مانو بدست می آید. بنابراین فلیپ فلاپ T فقط دو حالت دارد. وقتی T=0 باشد (J=K=0) یک گذار ساعت حالت فلیپ فلاپ را تغییر نمی دهد. وقتی T=1 باشد (J=K=1) انتقال ساعت حالت فلیپ فلاپ را متمم می کند. این حالات را می توان با معادله مشخصه زیر بیان ک
فلیپ فلاپ های تحریک شونده با لبه[14]
متداول ترین نوع فلیپ فلاپ های مورد استفاده در همگام کردن تغییر حالت به هنگام تغییر وضعیت با گذار پالس ساعت فلیپ فلاپ تحریک شونده با لبه (يا فلیپ فلاپ حساس به لبه) می باشد. در این نوع فلیپ فلاپ ها، تغییرات در خروجی بازاء سطح خاصی از ورودی پالس ساعت رخ می دهد. وقتی که سطح ورودی پالس ساعت از این سطح آستانه[15]تجاوز کند ورودی ها قفل می شوند بطوری که فلیپ فلاپ به تغییرات دیگر در ورودی، تا بازگشت پالس ساعت به 0 و ظهور پالس ساعتی دیگر، پاسخی نمی دهد. در بعضی از این نوع فلیپ فلاپ ها تأثیر ورودی ها در خروجی در لبه بالا رونده سیگنال ساعت (گذار یا انتقال در لبه مثبت) و برخی نیز در لبه پایین (گذار در لبه منفی) میسر است.
(الف) سمبل گرافیکی
(ب) جدول مشخصه
شکل 22-1 فلیپ فلاپ T

(الف) فلیپ فلاپ D تحریک شونده با لبه مثب
(ب) فلیپ فلاپ D تحریک شونده با لبه منفی
شکل ۲۳-۱ فلیپ فلاپ تحریک شونده با لبه
شکل 23-1 (الف) سیگنال پالس ساعت را در یک فلیپ فلاپ D حساس به لبه مثبت نشان می دهد. مقدار ورودی Dدر لبه مثبت پالس ساعت به خروجی Qمنتقل می شود. هنگامی که پالس ساعت در سطح 1 در سطح 0 یا در حال انتقال از سطح 1 به 0 باشد خروجی تغییری نمی کند. گذار یا انتقال مثبت پالس شامل دو فاصله زمانی است که یکی حداقل زمان آماده سازی[16] می باشد و طی آن ورودی D باید در یک سطح ثابتی قبل از گذار پالس ساعت دانلود کتاب معماری کامپیوتر موریس مانو بماند و دیگری زمان معینی با نام زمان نگهداری[17]است که طی آن ورودی D نباید پس از گذار پالس ساعت تغییر کند. زمان مربوط به انتقال یا گذار مثبت کسر بسیار کوچکی از کل دوره تناوب پالس ساعت است.
شکل ۲۳-۱ (ب) سمبل های گرافیکی و دیاگرام زمانی مربوط به فلیپ فلاپ D حساس به لبه منفی را نشان می دهد. در سمبل گرافیکی، یک دایره کوچک منفی کننده[18]در جلو علامت دینامیکی در ورودی Cقرار دارد. این علامت بیانگر تحریک فلیپ فلاپ در لبه منفی پالس است. در این حالت پاسخ فلیپ فلاپ در قبال انتقال سطح سیگنال ساعت از سطح 1 به 0 می باشد.
نوع دیگری از فلیپ فلاپ که در بعضی از سیستم ها بکار می رود فلیپ فلاپ ماستر - اسليو[19](بمعنی حاکم و پیرو) است. این نوع مدار از دو فلیپ فلاپ تشکیل شده است. اولین فلیپ فلاپ ماستر نامیده می شود و به سطح مثبت پالس ساعت پاسخ می دهد، و دومین فلیپ فلاپ اسلیو می باشد که به سطح منفی پالس ساعت واکنش نشان می دهد. در نتیجه خروجی بهنگام تغيير 1 به 0 سیگنال ساعت تغییر می نماید. امروزه گرایش در کنار گذاشتن فلیپ فلاپ ماستر - اسليو و بکارگیری فلیپ فلاپ حساسی به لبه دیده می شود.
فلیپ فلاپ های موجود بصورت مدار مجتمع گاهی دارای پایانه های خاصی برای نشاندن[20] و پاک کردن[21]غیر همگام[22]می باشند. این ورودی ها معمولا نشاندن اولیه[23] و پاک کردن نامیده می شوند و با سطح منفی سیگنال ورودی خود بدون نیاز به پالس ساعت بر فلیپ فلاپ اثر می گذارند. این ورودی ها برای قرار دادن فلیپ فلاپها در یک وضعیت اولیه قبل از شروع بکار با پالسی ساعت مفیدند.
جداول تحریک
جداول تحریک فلیپ فلاپ ها حالت بعدی را هرگاه ورودی ها و حالت فعلی معلوم باشند مشخص می کنند. معمولا هنگام طراحی مدارهای ترتیبی انتقال از حالت فعلی به حالت بعدی برای ما شناخته شده است و ما مایلیم تا ورودی های فلیپ فلاپ را طوری بیابیم که انتقال مناسب انجام یابد. به همین دلیل به جدولی نیاز داریم که بر حسب تغيير مفروضی در حالت ورودی های مورد نیاز را نشان دهد چنین لیستی از حالت ها،جدول تحریک فلیپ فلاپ نامیده می شود.
ورودی های مورد نیاز برای هر یک از چهار انتقال از اطلاعات موجود در جدول مشخصه بدست آمده اند.سمبل X در جداول نشان دهنده حالت بی اهمیت است و باین معنی است که 0 یا 1 بودن ورودی مهم نیست.
دلیل وجود حالات بی اهمیت در جداول تحریک این است که برای دستیابی به یک انتقال مورد نظر دو راه وجود دارد. مثلا در یک فلیپ فلاپ JK ، انتقال از حالت فعلی 0 به حالت بعدی را می توان با قرار دادنJ و K در حالت 0 (برای حالت بالاتغییر) یا با قرار دادن J=0 و K=1برای پاک کردن فلیپ فلاپ (گرچه از قبل پاک شده است) بدست آورد. در هر دو مورد J باید 0 باشد ولی K در مورد اول 0 در مورد دوم 1 است. چون در هر صورت انتقال مورد نظر رخ خواهد داد، ما ورودی K را با X علامت میزنیم و لذا طراح اجازه خواهد داشت مقدار ما را با توجه به اینکه کدام مناسبتر است، 1 یا 0 انتخاب کند.
1-7 مدارهای ترتیبی
مدار ترتیبی از اتصال مجموعه ای از فلیپ فلاپها و گیت ها بوجود می آید. گیت ها به تنهایی مدارهای ترکیبی را تشکیل می دهند ولی وقتی با فلیپ فلاپها همراه باشند مدار حاصل از رده مدارهای ترتیبی خواهد بود. بلوک دیاگرام یک مدار ترتیبی ساعت دار در شکل ۲۴-۱ نشان داده شده است. این مدار از یک مدار ترکیبی و تعدادی فلیپ فلاپ ساعت دار تشکیل شده است. بطور کلی، هر تعداد یا هر نوع فلیپ فلاپ می تواند در مدار بکار رود، همانطور که در دیاگرام نشان داده شده است، بلاک مدار ترکیبی سیگنالهای دودویی را از ورودی های خارجی و از خروجی های فلیپ فلاپها دریافت می کنند. خروجی های مدار ترکیبی به خروجی های خارجی و به ورودی های قلیپ فلاپها می روند. گیت های تشکیل دهنده مدار ترکیبی مقادیر ذخیره شونده در فلیپ فلاپها را بعد از هر گذار پالس ساعت معین می کنند. خروجی فلیپ فلاپها به نوبه خود به ورودی های مدار ترکیبی اعمال شده و رفتار مدار را تعیین می کنند. این فرآیند نشان می دهد که خروجی های خارجی مدار ترتیبی تابعی از ورودی های خارجی و حالت فعلی[24]فلیپ فلاپها است. بعلاوه، حالت بعدی[25]فلیپ فلاپها نیز تابعی از حالت فعلی آنها و ورودی های خارجی می باشد. بنابراین یک مدار ترتیبی با یک رشته ورودی های زمانبندی شده، خروجی های خارجی و حالات دودویی فلیپ فلاپهای داخلی اش مشخص می گردد.
معادلات ورودی فلیپ فلاپها [26]
مثالی از یک مدار ترتیبی در شکل ۲۵-۱ دیده می شود. این مدار دارای یک متغیر ورودی x، یک متغیر خروجی لاو دو فلیپ فلاپ Dساعت دار است. گیت های OR ،AND و معکوس کننده بخش ترکیبی مدار منطقی را تشکیل می دهند. اتصالات بین گیت ها در مدار ترکیبی می تواند بوسيله مجموعه ای از عبارات بولی مشخص گردد. بخشی از مدار ترکیبی که ورودی های فلیپ فلاپ را تولید میکنند بوسیله مجموعه ای از عبارات بولی که معادلات ورودی فلیپ فلاپها نام دارند توصیف می شود ما سمبل ورودی هر فلیپ فلاپ را بعنوان متغیر معادله ورودی و اندیس را برای مشخص کردن سمبل انتخاب شده بر می گزینیم.
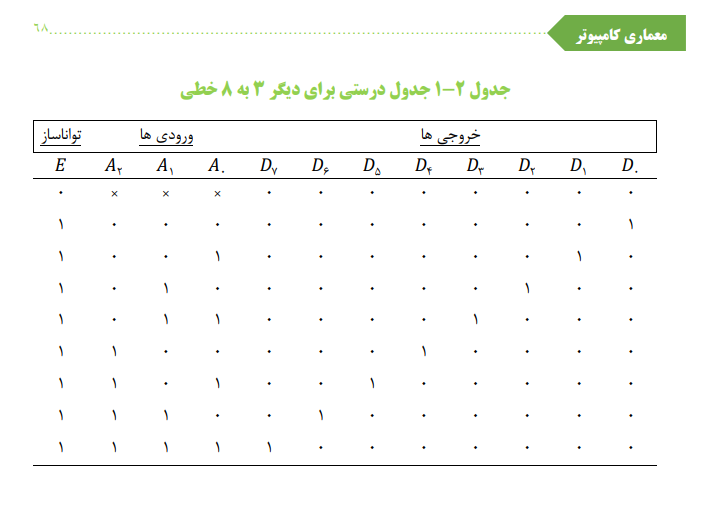
شكل ۲۵-۱ مثالی از یک مدار ترتیبی
بنابراین در شکل ۲۵-۱ ما دو معادله ورودی خواهیم داشت که با مشخص می شوند. اولین حرف در هر مورد نماینده ورودی D یک فلیپ فلاپ D حرف اندیس نام فلیپ فلاپ مربوطه است. معادلات ورودی، توابع بولی برای متغیرهای ورودی فلیپ فلاپ دانلود کتاب معماری کامپیوتر موریس مانو و از بررسی مدار بدست می آید. چون خروجی گیت OR به ورودی D از فلیپ فلاپ هم متصل شده است ما اولین معادله ورودی را می نویسیم
که A و B خروجی های دو فلیپ فلاپ و ورودی خارجی است، دومین معادله ورودی از خروجی گیت AND متصل به ورودی D فلیپ فلاپ B حاصل می شود
این مدار ترتیبی یک خروجی خارجی نیز دارد که تابعی از متغیر ورودی و حالات فلیپ فلاپها است. این خروجی می تواند بوسیله عبارت جبری زیر مشخص شود
از این مثال در می یابیم که یک معادله ورودی فلیپ فلاپ عبارتی بولی برای یک مدار ترکیبی است. متغير اندیس دار نام یک متغیر دودویی برای خروجی یک مدار ترکیبی است. این خروجی همواره به یکی از ورودی های فلیپ فلاپ ها متصل است.
جدول حالت[27]
رفتار یک مدار ترتیبی از ورودیها، خروجیها و حالت فلیپ فلاپ های آن معین می شود. خروجی ها و حالت بعدی تابعی از ورودی ها و حالت فعلی هستند، یک مدار ترتیبی توسط جدول حالتی مشخص می شود که خروجی ها و حالات بعدی را به صورت تابعی از ورودی و حالات فعلی مرتبط می سازد. در مدارهای ترتیبی ساعت دار انتقال از حالت فعلی به حالت بعدی بوسیله رخداد یک سیگنال ساعت ممکن می شود.
جدول حالت شكل ۲۵ -۱ در جدول ۴-۱ نشان داده شده است. جدول متشکل از چهار بخش است که با عناوین حالت فعلی، ورودی، حالت بعد و خروجی مشخص شده اند. بخش حالت فعلی حالات فلیپ فلاپ های A و B را در هر لحظه از زمان مفروض t نشان می دهد. بخش ورودی مقداری از x را در هر حالت فعلی معین می سازد. بخش حالت بعدی حالات فلیپ فلاپ ها را در پریود زمانی بعدي، t+1 بدست میدهد. بخش خروجی نیز مقدار y را در حالت فعلی و وضعیت ورودی می دهد.
در تشکیل یک جدول حالت، ابتدا لیست تمام ترکیبات دودویی حالت فعلی و ورودی را می نویسیم. در این حالت ما هشت ترکیب دودویی از 000 تا 111 خواهیم داشت. سپس مقادیر حالت های بعدی از دیاگرام منطقی یا از معادلات ورودی بدست می آیند. معادله ورودی برای فلیپ فلاپ هم برابر است با
مقدار حالت بعدي هر فیلپ دانلود کتاب معماری کامپیوتر موریس مانو برابر با مقدار ورودی D در حالت فعلی است. انتقال از حالت فعلی به حالت بعدی پس از اعمال سیگنال ساعت بوقوع می پیوندد. بنابراین هرگاه حالات فعلی و ورودی شرایط یا
را ایجاد کنند برابر 1 در نتیجه حالت بعدی A هم 1 خواهد شد.این مطلب در جدول حالت یا سه عدد 1 زیر ستون حالت بعدی A آورده شده است. بطور مشابه، معادله ورودی برای فلیپ فلاپ B با رابطه زیر داده می شود
حالت بعدی B در جدول حالت هنگامی 1 است که A برابر 0 برابر 1 باشد. ستون خروجی نیز از معادله خروجی زیر بدست می آید.
جدول حالت هر مدار ترتیبی با استفاده از روشی که در این مثال دیده شده بدست می آید، بطور کلی یک مدار ترتیبی m فلیپ فلاپ، n متغیر ورودی و p متغیر خروجی دارای m ستون حالت فعلی، n ستون برای ورودی ها، m ستون برای حالت بعدی و p ستون برای خروجی هاست، ستون های حالت فعلی و ورودی با هم ترکیب شده و ما ترکیب دودویی، از 0 تا -1 را در زیر آنها می نویسیم، ستون های حالت بعدی و خروجی توابعی از حالت فعلی و مقادیر ورودی بوده و مستقيما از مدار يا معادلات بولی که مدار را توصیف می کنند به دست می آیند.

اطلاعات موجود در جدول حالت را می توان بصورت گرافیکی در یک دیاگرام حالت نشان داد، در این نوع دیاگرام، یک حالت بوسیله یک دایره و انتقال بين حالات بوسیله خطوط جهت داری که دو ایر را بهم وصل می کنند نشان داده می شود، دیاگرام حالت مدار ترتیبی شکل ۲۵ -۱ در شکل ۲۶-۱ نشان داده شده است. دیاگرام حالت همان اطلاعات جدول حالت را در دسترس می گذارد. و مستقیما از جدول 4-1 بدست می آید. عدد دودویی داخل هر دایره حالت فلیپ فلاپ ها را مشخص می کند. در کنار خطوط جهت دار دو عدد دودویی که با ممیز از هم جدا شده اند نوشته شده است. اولین عدد مقدار ورودی را در حالت فعلی و عدد بعد از ممیز، خروجی را در همان حالت نشان می دهد. مثلأ كنار خط جهت داری که حالت 00 را به 01 وصل می کند 0/1 نوشته شده است، و بدان معنی است که وقتی مدار ترتیبی در حالت 00 است بازاء ورودی 1، خروجی 0 خواهد بود. پس از استعمال یک پالس ساعت، مدار به حالت یعلی الا می رود. همین اعمال پالس ساعت ممکن است ورودی را عوض کند. اگر ورودی شود خروجي 1 شده ولی اگر ورودی در 1 باقی بماند خروجي در 0 خواهد ماند. این اطلاعات از دیاگرام حالت و با دنبال کردن دو خط جهت داری که به دایره 01 وصل شده اند حاصل می گردد. خط جهت داری که دایره را به خودش وصل می کند نشان می دهد که تغییر حالتی رخ نداده است.
بين جدول حالت و دیاگرام حالت هیچ تفاوتی جز در نحوه نمایش وجود ندارد، بدست آوردن جدول حالت از دیاگرام منطقی آسان تر است و نمودار حالت مستقیما از جدول حالت بدست می آید دیاگرام حالت یک دید مصور را از انتقال حالات فراهم می نماید و بشکلی است که برای تفسیر عملکرد مدار مناسب تر می باشد. مثلا دیاگرام حالت شکل ۲-۱ بوضوح نشان می دهد که با شروع حالت از 00 مادامی که ورودی 1 است خروجی 0 خواهد بود. اولین ورودی 0پس از رشته ای از 1 ها، خروجی 1 تولید خواهد کرد و میدار را به حالت اولیه 00 بر می گرداند.
اکنون روش طراحی مدارهای ترتیبی بوسیله ارائه یک مثال خاص نشان داده می شود. در روش طراحی ابتدا مشخصات مدار را به یک دیاگرام حالت تبدیل می کنیم. سپس دیاگرام حالت به یک جدول حالت تبدیل می شود. بالاخره از جدول حالت برای تهیه دیاگرام مدار منطقی استفاده می شود.
ما می خواهیم یک مدار ترتیبی طراحی کنیم که هر وقت ورودی خارجی xبرابر 1 باشد رشته حالات دودودیی 00، 01،10 و 11 را تکرار نماید. بازاء x=0 هم حالت مدار تغییری نکند. این نوع مدار یک شمارنده دودویی دو بیتی است زیرا رشته حالات با شمارش متوالی دو رقم دودویی یکسان می باشد. ورودی x یک متغیر کنترل است که مشخص می کند شمارش چه زمانی آغاز شود.
شمارنده دودویی به دو فلیپ فلاپ برای نمایش دو رقم نیاز دارد. دیاگرام حالت برای مدار ترتیبی در شكل ۲۷ - ۱ نشان داده شده است. دیاگرام بدین منظور رسم شده است تا نشان دهیم مادامی که x=1 است مدار شمارش دودویی را ادامه می دهد. حالت بعد از 11 ، حالت 00 است که باعث تکرار شمارش می گردد. اگر x=0 باشد، حالت مدار بدون تغییر باقی می ماند. این مدار ترتیبی خروجی خارجی ندارد و بنابراین فقط مقدار دودویی در جوار خطوط واصل در دیاگرام نوشته شده است. در این مدار حالت فلیپ فلاپها بعنوان خروجی های شمارنده تصور شده اند.
ما قبلا سمبل x را به متغیر ورودی اختصاص دادیم. حال سمبل های A و B را به خروجی های دو فلیپ فلاپ تخصیص می دهیم. حالت بعدی A و B را، می توان بعنوان تابعی از حالت فعلی و ورودی x، از دیاگرام حالت به جدول حالت منتقل ساخت. پنج ستون اول جدول ۵-۱ جدول حالت را بوجود می آورند. وارده های این جدول مستقیما از دیاگرام حالت بدست می آیند.
شكل ۲۷-۱ دياگرام حالت برای شمارنده دودویی
جدول تحریک یک مدار ترتیبی نوع تعمیم یافته یک جدول حالت است. این تعمیم شامل لیستی از تحریک های ورودی فلیپ فلاپ می باشد که موجب انتقال به حالت مورد نظر می شوند، شرایط ورودی فلیپ فلاپها تابعی از نوع فلیپ فلاب بکار رفته می باشد. ما اگر از فلیپ فلاپهای JK استفاده کنیم، نیاز به ست و نشان داده می شوند.
دیاگرام منطقی که در شکل ۲۹-۱ رسم شده است از دو فلیپ فلاپ JKو یک گیت AND تشکیل یافته است. توجه کنید که ورودی های J و K حالت بعیدی دانلود کتاب معماری کامپیوتر موریس مانو را پس از وقوع پالس ساعت معین می کنند. اگر هر دو ورودی J و K برابر 0 باشند پالس ساعت تأثیری نخواهد داشت. یعنی حالت فلیپ فلاپ ها تغییری نمی کند. بنابراین وقتي x=0 باشد، تمام ورودی های فلیپ فلاپ ها برابر 0 و حالت فلیپ فلاپها بلا تغییر باقی می مانند حتی اگر پالسهای ساعت مرتبا به مدار اعمال شوند.
شکل ۲۹-۱ دياگرام منطقی یک شعارنده دو بیتی
روش طراحی
طراحی مدارهای ترتیبی رئوس مطالبی را که در مثال طراحی دیده شد دنبال می کند. ابتدا رفتار مدار بصورت دیاگرام حالت فرموله می شود. تعداد فلیپ فلاپ های لازم برای مدار با توجه به تعداد بیت های داخل دایره ها در دیاگرام حالت معین می گردد. تعداد ورودی ها برای مدار در امتداد خطوط وأصل بين دایره ها مشخص می شود. ما سپس حروفی را برای علامت گذاری تمام فلیپ فلاپها، متغیرهای ورودی و خروجی بکار گرفته و برای بدست آوردن جدول حالت به مرحله بعد می رویم.
بازاء m فلیپ فلاپ و n ورودی، جدول حالت شامل m ستون برای حالت فعلی، n ستون برای ورودی ها و mm متون برای حالت بعدی خواهد بود. تعداد سطرهای جدول ت می باشد که هر سطر مربوط به یک ترکیب دودویی از حالت فعلی و ورودی هاست. در هر سطر با حالت بعدی را آنچنانکه در دیاگرام حالت مشخص شده لیست میکنیم. سپس نوع فلیپ فلاپ بکار رفته در مدار انتخاب می شود. جدول حالت به جدول تحریک یا اضافه کردن ستونهای هر ورودی در هر فلیپ فلاپ تعميم می یابد. جدول تحریک برای فلیپ فلاپ بکار رفته می تواند از جدول ۳-۱ بدست آید. از اطلاعات موجود در این جدول و با بررسی انتقال حالت فعلی به حالت بعدی در جدول حالت اطلاعات مربوط به شرایط ورودی فلیپ فلاپها را در جدول تحریک بدست می آوریم.
جدول درستی بخش ترکیبی مدار ترتیبی در جدول تحریک موجود است. ستونهای حالت فعلی ورودی ها، ورودی های جدول درستی را تشکیل می دهند. وضعیت ورودی فلیپ فلاپها خروجی های جدول درستی را تشکیل می دهند. با استفاده از مفهوم ساده سازی بکمک نقشه، ما مجموعه ای از معادلات ورودی فلیپ فلاپها را برای مدار ترکیبی بدست می آوریم. هر معادله ورودی فلیپ فلاپ یک نمودار منطقی را مشخص می کند که خروجی آن باید به یکی از ورودی های فلیپ فلاپها وصل شود. مدار ترکیبی حاصل، همراه با فلیپ فلاپهاء مدار ترتیبی را تشکیل می دهد.
اغلب، خروجی فلیپ فلاپها بعنوان بخشی از خروجی های مدار ترتیبی تصور می شوند. با این وجود مدار ترکیبی ممکن است خروجی خارجی هم داشته باشد. در چنین حالتی توابع بولی خروجی های خارجی از جدول حالت با کمک تکنیک های طراحی بدست می آیند.
مجموعه ای از معادلات ورودی فلیپ فلاپها یک مدار ترتیبی را بفرم جبری مشخص می کنند، روش یافتن دیاگرام منطقی از مجموعه معادلات ورودی فلیپ فلاپها یک روند مستقیم و سر راست است. ابتدا تمام ورودی ها و خروجی ها را نامگذاری می کنیم. سپس مدار ترکیبی را با توجه به معادلات بولی حاصل از معادلات ورودی فلیپ فلاپها رسم می نمائیم. و بالاخره خروجی های فلیپ فلاپها را به ورودی های مدارت ترکیبی و خروجی های مدار ترکیبی را به ورودی های فلیپ فلاپها وصل می نمائیم.
(الف) جدول درستی تابع را بدست آورید.
(ب) دیاگرام منطقی را با استفاده از عبارت بولی اصلی رسم کنید.
(ج) عبارت جبری را با بکارگیری جبر بول پیاده کنید.
(د) جدول درستی را با استفاده از عبارت ساده شده تابع تشکیل داده و نشان دهید که همان جدول بخش (الف) است.
(هـ) دیاگرام منطقی را با استفاده از عبارت ساده شده بدست آورده و تعداد کل گیت ها را با دیاگرام بخش (ب) مقایسه کنید
15-1 یک مدار ترتیبی بنام تابع اکثریت بدین صورت تعریف می شود که هرگاه مقدار متغیرهای ورودی 1بیشتر از ورودی های 0 باشند خروجی 1 است. تابع اکثریت سه ورودی را طراحی کنید.
16-1 یک مدار ترکیبی با سه متغير x.y.z و سه خروجی A.B.C طراحی کنید. اگر ورودی های دودویی 3.2.1.0 باشد خروجی یکی بیشتر از ورودی است. وقتی ورودی ها 4، 4، 6 و 7 باشند خروجی دودویی یکی کمتر از ورودی باشند.
17-1 نشان دهید که یک فلیپ فلاپ JK را با قرار دادن یک معکوس کننده بین ورودی های J و K می توان به یک فلیپ فلاپ D تبدیل کرد.
18-1 با استفاده از اطلاعات موجود در جدول مشخصه فلیپ فلاپ JK در جدول شکل ۲-۱ (ب) جدول تحریک را برای فلیپ فلاپ JK بدست آورده و جواب خود را با جدول ۳-۱ مقایسه کنید.
19-1 یک مدار ترتیبی دارای دو فلیپ فلاپ A و B، در ورودی x و y و یک خروجی z است.معادلات ورودی فلیپ فلاپ و نیز خروجی مدار بقرار زیرند:
الف) دیاگرام منطقی را برای مدار رسم کنید
ب) جدول حالت را برپا کنید.
20-1 یک پایین شمار دو بیتی را طراحی کنید، این یک مدار ترتیبی دارای دو فلیپ فلاپ و یک وروردی X می باشد. وقتی x= 0 است حالت فلیپ فلاپ تغییر نمی کند. وقتی x= 1 باشد ترتیب حالات 11، 10، 01، 00 و 11 و تکرار آن خواهد بود.
21-1 یک مدار ترتیبی با دو فلیپ فلاپ JK و دو ورودی E و X طراحی کنید. اگر E=0 باشد، مدار بدون توجه به مقدار در همان حالت باقی می ماند. وقتی E=1 و x=1 است مدار به یک سری حالات از 00 به 01، به 10، به 11 و 00 و تکراری از آن وارد می شود. وقتی E=1 و x=0 باشد مدار به حالات انتقالی 00 به 11، به 01 و 00 و تکراری از آن وارد می شود.
فصل دوم
قطعات دیجیتال
1-2 مدارهای مجتمع
2-2 دیکدرها
3-2 مولتی پلکسرها
4-2 ثبات ها
5-2 شیفت رجیسترها
6-2 شمارنده های دودویی
7-2 واحد حافظه
1-2مدارهای مجتمع[28]
مدارهای دیجیتال با مدارهای مجتمع ساخته می شوند. یک مدار مجتمع (یا آی سی)، یک کریستال کوچک نیمه هادی بنام تراشه[29]است که قطعات دانلود کتاب معماری کامپیوتر موریس مانو را برای گیتهای دیجیتال در خود دارد. اتصالات داخل تراشه، مدار مورد نیاز را بوجود می آورد. تراشه در داخل یک محفظه پلاستیک و یا سرامیک جاسازی می شود و اتصالات آن با سیم های طلایی نازک به پایه های خارجی جوش داده می شود تا مدار مجتمع بوجود آید. تعداد پایه ها ممکن است از 14 پایه در بسته های کوچک تا 100 پایه یا پیشتر در بسته های بزرگتر تغییر کند. هر میدار مجتمع یا آی سی دارای یک مشخصه عمل دی است که روی سطح بسته بندی آن برای شناسایی چاپ می شود. هر سازنده یک کتابچه راهنما یا کاتالوگ با شرح دقیق و تمام اطلاعات لازم درباره آی سی های ساخت خود را چاپ می کند.
با پیشرفت تکنولوژی مدارهای مجتمع، تعداد گیت هایی که می توانست در یک تراشه جای گیرد به میزان قابل ملاحظه ای افزایش یافت. تراشه هایی که دارای چند گیت داخلی بودند و آن دسته که چند صد گیت را دارا بودند در بسته هایی با ظرفیت یا مقیاس کوچک، متوسط و یا بزرگ جای داده شدند.
مدارهای مجتمع با مقیاس کوچک[30] (SSI) دارای چند گیت مستقل در یک بسته وأحد هستند ورودی ها و خروجی های گیت ها مستقیما به پایه های بسته متصل اند، تعداد گیت ها معمولا کمتر از ۱۰ و محدود به تعداد پایه ها در IC میباشد.
قطعات مجتمع با مقیاس متوسط[31] (MSI) دارای تقریبأ ۱۰ الی ۲۰۰ گیت در هر بسته می باشند. این وسیله ها معمولا توابع دیجیتال ساده همچون دیکدرها، جمع کننده ها و ثبات ها را اجرا می نمایند. مدارها با وسایل مجتمع با مقیاس بزرگ[32] (LST) بین ۲۰۰ تا چند هزار گیت در هر بسته دارند. این بسته ها سیستم های دیجیتالی همچون پردازنده ها، تراشه های حافظه و ماژول های قابل برنامه ریزی را شامل می شوند. قطعات مجتمع با مقیاس بسیار بزرگ[33] (VLSI) حاوی هزاران گیت در یک بسته اند. مثالهایی از این گروه عبارتنداز، آرایه های بزرگ حافظه و تراشه های پیچیده ریز کامپیوترها. VLSIها بدلیل کوچکی و ارزانی انقلابی در تکنولوژی ساخت سیستم های کامپیوتری بوجود آورده و به طراحان امکان ساخت و ایجاد ساختارهایی را دادند که قبلا اقتصادی نبودند.
مدارهای مجتمع ديجيتال نه تنها براساس عملکرد منطقی شان طبقه بندی می شوند بلکه از نظر تکنولوژی خاص مدارهایی که به آن تعلق دارند نیز دسته بندی می گردند. تکنولوژی بکار رفته در مدار را خانواده منطقی دیجیتال[34] می خوانند. هر خانواده منطقی، مدار الکترونیکی پایه خاصی را داراست که میدارها و توابع دیجیتال پیچیده تر براساس آن تهیه می شوند. مدار پایه در هر تکنولوژی یک گیت NOR NAND و یا معکوس کننده است، در نام گذاری تکنولوژی از قطعات الکترونیک بکار رفته در ساخت مدار پایه معمولا استفاده می شود. بسیاری از خانواده های مختلف منطقی بصورت مدارهای مجتمع در سطح تجاری عرضه شده اند. متداول ترین خانواده ها در زیر معرفی شده اند.
TTL- منطق ترانزیستور – ترانزیستور[35]
ECL- منطق کوپل اميتر[36]
MOS- منطق فلز - اکسید - نیمه هادی[37]
CMOS- منطق فلز - اکسید - نیمه هادی مکمل[38]
TTL یک خانواده متداول است که سالها مورد استفاده بوده و بعنوان استاندارد تلقی می شود، ECL در سیستم هایی که به سرعت عمل بالا نیاز دارند ترجیح داده می شود. MOS برای مدارهایی که نیاز به تراکم بالا دارند مناسب است، وي CMOS در سیستم های کم مصرف بکار می رود.
خانواده منطقی ترانزیستور - ترانزیستور گونه تکامل یافته تکنولوژی قدیمیتری است که در آن از دیود و ترانزیستور برای ساخت گیت پایه NAND استفاده می شده است. این تکنولوژی منطق دیود - ترانزیستور[39] (DTL) خوانده می شده است، بعدها برای بهبود عملکرد مدار بجای ديود از ترانزیستور استفاده شد و نام خانواده جدید، منطق ترانزیستور - ترانزیستور گذاشته شد. بهمین دلیل نام ترانزیستور در این عبارت دو بار تکرار شده است. علاوه بر نوع استاندارد TTL، انواع دیگری از این خانواده عبارتند از: TTL سرعت بالا[40]،TTL توان پائین[41] (یا کم مصرف) ، TTL شو تکی[42] ، TTL شو تکی توان پایین[43] و TTL شو تکی پیشرفته[44]. منبع تغذیه مدارهای TTL دولت است و در سطح منطقی تقریبأ 0 و 5/3 ولت می باشند.
خانواده کوپل امیتر سریع ترین مدارهای دیجیتال را بفرم مجتمع در اختیار می گذارد. ECL در مدارهایی مانند سوپر کامپیوترها و پردازنده های سیگنال که در آنها سرعت بالا ضرورت دارد، بکار می رود. ترانزیستورها در گیت های ECL در حالت غیر اشباع کار می کنند و رسیدن به تأخیرهای انتشاری در حد ۱ تا ۲ نانو ثانیه در آنها میسر است.
منطق فلز - اکسید - نیمه هادی (MO5) یک ترانزیستور تک قطبی است که به جریان یک نوع حامل الکتریکی وابسته است. این حامل ها ممکن است الكترون در نوع کانال n یا حفره در نوع کانال P باشند. این، برخلاف ترانزیستور دو قطبی بکار رفته در گیت های TTL و ECL است، که در حین عملکرد هر دو نوع حامل در آن وجود دارند. یک MOS کانال P را PMOS و یک MOS کانال n را NMOS می نامند. معمولا در مدار هایی که فقط یک نوع ترانزیستور MOS وجود دارد از NMO5 استفاده می شود. در تکنولوژی CMOS هر دو نوع ترانزیستور PMOS وNMOS که بشكل مکمل در تمام میدارها بسته شده اند بکار رفته است. بزرگترین مزیت CMOS نسبت به دو قطبی تراکم بالای مدار ها در بسته بندی، ساده بودن تکنیک ساخت و عملكرد مقرون به صرف آن بدلیل مصرف توان كم است.
بعلت مزایای بیشمار، مدارهای مجتمع انحصارا در تهیه انواع قطعات لازم در طراحی سیستم های کامپیوتر به کار می روند. برای درک سازمان و دانلود کتاب معماری کامپیوتر موریس مانو کامپیوترها، آشنایی با انواع قطعات و اجزاء بکار رفته در مدارهای مجتمع اهمیت دارد. به این دلیل، اجزاء اصلی به همراه خواص منطقی آنها تشریح شده است. این اجزاء مجموعه ای از واحدهای عملیاتی دیجیتال را فراهم می کنند که در طراحی کامپیوترهای دیجیتال بعنوان پلاک های ساختمانی اصلی (پایه) به کار می روند
۲-۲ ديکدرها[45]
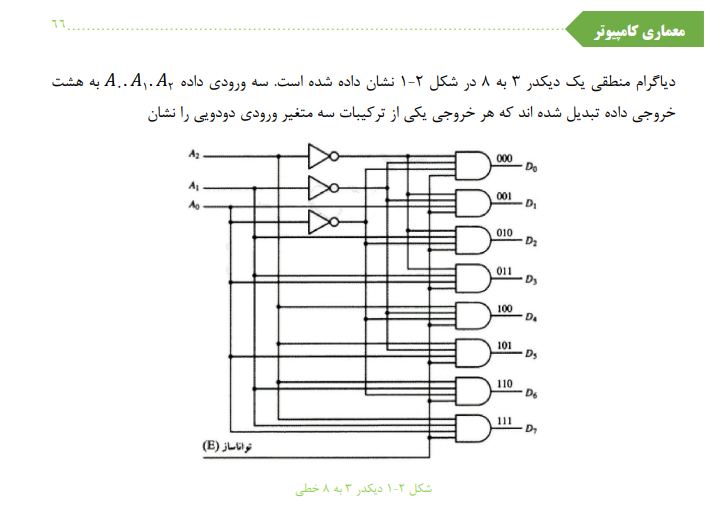
شکل ۱-۲ ديکدر 3 به 8 خطی
می دهد. سه معکوس کننده، متمم ورودی ها را فراهم میکنند و هر یک از هشت گیت AND یکی از ترکیبات دودویی را تولید می نماید. کاربرد خاصی از این دیکدر تبديل دودویی به هشتایی است متغیرهای ورودی یک عیلاد دودویی را نشان می دهند و خروجی ها، هشت رقم یک عدد سیستم هشتایی[46]را نمایش می دهند. با این وجود یک دیکدر 3 به 8 خطی می تواند برای دیکد کردن هر کد سه بینی بکار رفته و هشت خروجی را که هر بار یکی از ترکیبات کل دودویی است، فراهم آورد.
دیکدرهای تجاری دارای یک یا چند ورودی تواناسازی[47]فعال سازی برای کنترل کار مدار هستند. دیکدر شکل ۱-۲ دارای یک ورودی تواناساز،E می باشد. دیکدر هنگامی فعال شده است که E برابر 1 باشد و اگر نا مساوی بود دیکدر ناتوان (غیرفعال) شده است. عملکرد دیکدر با استفاده از یک جدول درستی که در جدول ۱-۲ دیده می شود آشکارتر خواهد شد. هرگاه ورودی تواناساز E برابر 0 باشد تمام خروجی ها، بدون توجه به مقادیر به ورودی داده خواهند شد. سه علامت در جدول حالات بی اهمیت ورودی ها را نشان مي دهند. اگر ورودی تواناساز، 1 شود، دیکدر در وضع عادی خودکار خواهد کرد. برای هر ترکیب ممکن ورودی، هفت خروجی 0 و فقط یک خروجی 1وجود دارد که بیانگر عدد هشتایی معادل عدد دودویی در خطوط ورودی داده است.
دیکدر با گیت NAND
بعضی از دیکدرها بجای گیت AND با گیت NAND ساخته می شوند. چون گیت NAND عمل گیت AND را با خروجی معکوس شده انجام می دهید، تولید خروجی های معکوس شده با دیکدر مقرون به صرفه تر است. یک دیکدر 2 به 4 همراه با ورودی توانا ساز که از گیت های NAND ساخته شده است در شکل ۲-۲ نشان داده شده است. مدار دارای خروجی های متمم بوده و با ورودی تواناساز متمم شده کار می کند. دیکدر هنگامی تواناست که E برابر 0 شود. همانطور که از جدول درستی پیداست، تنها در هر لحظه از زمان فقط یک خروجی برابر ، و بقیه سه خروجی دیگر برابر 1 هستند. خروجی که نماینده عدد دودویی واقع در ورودی های
است دارای مقدار لا است. هر گاه E برابر 1 باشد، مدار صرف نظر از مقدار دودویی ورودی های دیگری غیر فعال خواهد بود. وقتی که مدار غیر فعال است، هیچ یک از خروجی ها انتخاب نمی شود و تمام خروجی ها برابر 1 خواهد بود، بطور کلی، یک دیکدر ممكن است با خروجی های متمم شده یا نشده کار کند. ورودی تواناساز هم ممکن است با یک سطح سیگنال لایا 1 فعال شود. برخی دیکدرها دارای دو یا چند ورودی تواناساز هستند و برای فعال شدن مدار شرایط منطقی معینی باید در آنها برقرار باشد.
دانلود کتاب مدیریت منابع انسانی گری دسلر
انكدرها[48]
انکدر (کدگذار) یک مدار دیجیتال است که عکس عمل دیکدر را انجام می دهد. یک انکدر دارای (یا کمتر) خط ورودی و n خط خروجی است. خطوط خروجی کد دودویی متناظر مقدار ورودی را تولید می کنند، مثالی از یک انکدر، انکدر هشت هشتی به دودویی است، که جدول درستی آن در جدولی ۲-۲ داده شده است. این مدار دارای هشت ورودی، که هر یک به یک رقم هشت هشتی (هشتایی) متعلق بوده و سه خروجی که عدد دودویی متناظر را تولید می کنند، است. فرض بر این است که فقط یک ورودی دارای مقدار 1 در هر لحظه از زمان است؛ در غیر این صورت مدار مفهومی ندارد.
انكدر را می توان با گیت های OR که ورودی هایشان مستقیما از جدول درستی تعیین می شوند
پیاده سازی کرد، خروجي مي بشرطى 1 است که رقم ورودی هشت هشتی 1 یا 3 یا 5 یا 7 باشد. شرایط مشابهی برای دو خروجی دیگر برقرار است، این شرایط را می توان بوسیله توابع بولی زیر بیان کرد.