ازدواج پایدار؛ مسئله‌ای ساده اما عمیق

به قلم عتید خدایی، ورودی ۴۰۰ مهندسی کامپیوتر دانشگاه صنعتی اصفهان
بازنگری‌شده توسط پارسا شیرکوند و سارا چترایی، ورودی ۴۰۲ و ۴۰۰ کارشناسی مهندسی کامپیوتر صنعتی اصفهان

در این مطلب، قصد داریم درباره‌ی یک مسئله‌ی جالب ریاضی صحبت کنیم که درک آن نیازی به دانستن مشتق، انتگرال یا حتی ریاضیات دبیرستان ندارد؛ مسئله‌ی ازدواج پایدار!

تصور کنید دو گروه هم‌اندازه دختر و پسر داریم.
هر فرد در هر گروه، اولویت‌های خاص خود را برای انتخاب شریک زندگی از گروه مقابل دارد. هدف ما این است که یک مجموعه از ازدواج‌های پایدار بر اساس این اولویت‌ها پیدا کنیم. اما اصلاً ازدواج پایدار یعنی چه؟

بیایید مفهوم پایداری را بررسی کنیم. فرض کنید هر پسر با یک دختر جفت شده است. حالا اگر در این مجموعه، یک دختر (مثلاً آذر) و یک پسر (مثلاً بابک) وجود داشته باشند که با یکدیگر جفت نشده‌اند، اما هر دو یکدیگر را به همسر فعلی خود ترجیح می‌دهند، آنگاه یک ناپایداری رخ داده است. چنین وضعیتی مطلوب نیست، زیرا ممکن است این دو نفر، زوجیت خود را به هم زده و به سمت یکدیگر متمایل شوند. بنابراین، در یک ازدواج پایدار، هیچ دو نفری نباید وجود داشته باشند که همدیگر را به همسر فعلی‌شان ترجیح دهند.

در سال ۱۹۶۲، گیل و شاپلی مقاله‌ای تحت عنوان "College Admissions & The Stability of Marriage" منتشر کردند که در آن، الگوریتمی برای یافتن مجموعه‌ای از زوج‌ها به‌گونه‌ای که هیچ ناپایداری رخ ندهد، معرفی شد.

بیایید برای درک بهتر این الگوریتم، یک مثال ساده از مقاله‌ی گیل و شاپلی را بررسی کنیم. فرض کنید چهار پسر به نام‌های آلفا، بتا، گاما و دلتا و چهار دختر به نام‌های A, B, C, D داریم.

هر فرد لیستی از اولویت‌های خود را برای انتخاب همسر دارد. این اولویت‌ها را می‌توان در یک ماتریس رتبه‌بندی نمایش داد. در این ماتریس، هر عدد نشان‌دهنده‌ی رتبه‌ای است که یک پسر به یک دختر اختصاص داده است. مثلاً اگر آلفا دختر A را در رتبه‌ی اول و دختر D را در رتبه‌ی آخر قرار دهد، یعنی از نظر او A بهترین گزینه و D نامطلوب‌ترین گزینه است.

چگونه ازدواج‌های پایدار را بیابیم؟

بیایید ببینیم چگونه می‌توان یک مجموعه از ازدواج‌های پایدار را پیدا کرد. برای این کار، از الگوریتم گیل-شاپلی استفاده می‌کنیم که در آن پسرها به دخترها پیشنهاد ازدواج می‌دهند.

۱. مرحله اول پیشنهادهای اولیه ارسال می‌شود. هر پسر به اولین دختری که در لیست اولویت‌هایش قرار دارد پیشنهاد ازدواج می‌دهد.

• آلفا → A
• بتا → A
• گاما → B
• دلتا → D

۲. در مرحله دوم پیشنهادها توسط دختران بررسی می‌شود. هر دختر از میان پیشنهادهایی که دریافت کرده، کسی را انتخاب می‌کند که برایش اولویت بالاتری دارد و بقیه را رد می‌کند:

• دختر A پیشنهاد آلفا را قبول می‌کند و به بتا پاسخ منفی می‌دهد.
• دختر B تنها یک پیشنهاد (از گاما) دریافت کرده، پس آن را قبول می‌کند.
• دختر D تنها پیشنهاد دلتا را دریافت کرده، پس آن را می‌پذیرد.

۳. در مرحله سوم درخواست جدید از طرف پسری که رد شده است ارسال می‌شود. یعنی حالا پسری که رد شده است (بتا)، به دختر بعدی در لیست اولویت‌هایش پیشنهاد می‌دهد:

• بتا → D

۴. مجددا درخواست‌ها توسط دختران بررسی می‌شود.

• دختر D حالا دو پیشنهاد دارد: بتا و دلتا. او کسی را انتخاب می‌کند که در لیست اولویت‌هایش جایگاه بالاتری دارد. بتا را انتخاب می‌کند و دلتا را رد می‌کند.
• دلتا که رد شده است، حالا به اولویت بعدی خودش درخواست می‌دهد:
• دلتا → B

۵. چرخه ادامه پیدا می‌کند.

• دختر B حالا دو پیشنهاد دارد: دلتا و گاما. او دلتا را ترجیح می‌دهد و گاما را رد می‌کند.
• گاما که رد شده است، به اولویت بعدی‌اش درخواست می‌دهد:
• گاما → A
• دختر A حالا دو پیشنهاد دارد: آلفا و گاما. او گاما را انتخاب می‌کند و آلفا را رد می‌کند.
• آلفا که رد شده است، به اولویت بعدی‌اش درخواست می‌دهد:
• آلفا → B
• دختر B هنوز پسر دلتا را ترجیح می‌دهد، پس آلفا را رد می‌کند.
• آلفا که باز هم رد شده است، به اولویت بعدی‌اش درخواست می‌دهد:
• آلفا → C
• دختر C تا این لحظه هیچ پیشنهاد دیگری دریافت نکرده است، بنابراین پیشنهاد آلفا را می‌پذیرد.

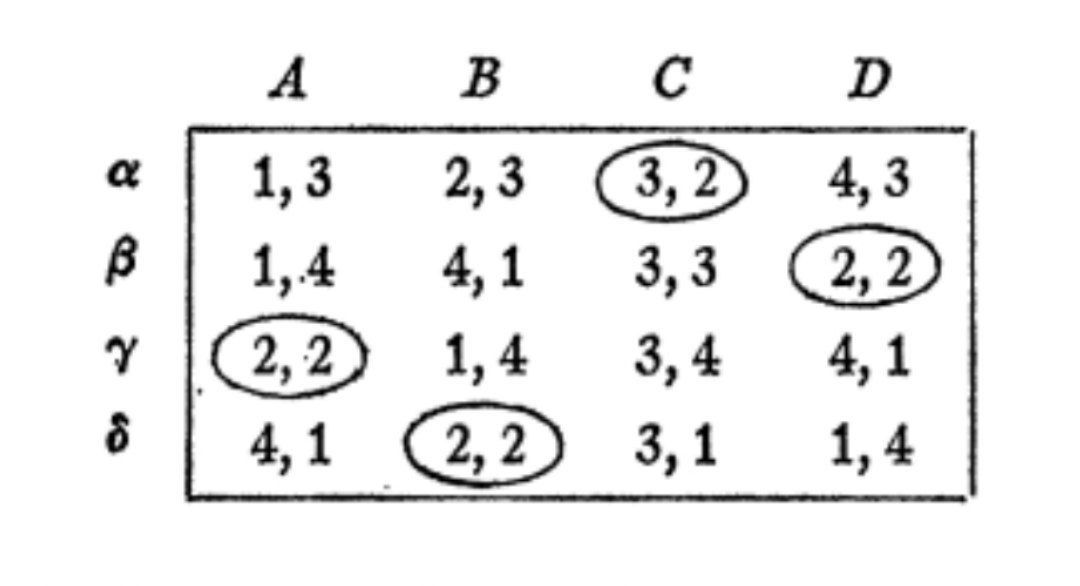
بعد از این مراحل، همه‌ی افراد با یک زوج مطابق با الگوریتم جفت شده‌اند و دیگر هیچ پسر یا دختری نیست که کسی را خارج از این مجموعه ترجیح دهد که او هم متقابلاً همان احساس را داشته باشد. بنابراین، این یک مجموعه ازدواج پایدار است.

کاربردهای الگوریتم ازدواج پایدار در دنیای واقعی

الگوریتم گیل-شاپلی فقط یک مسئله‌ی ریاضی نیست؛ بلکه در سیستم‌های مختلفی برای تخصیص منابع و ایجاد مچینگ‌های بهینه مورد استفاده قرار می‌گیرد. در اینجا دو نمونه‌ی مهم از کاربردهای این الگوریتم را بررسی می‌کنیم: پذیرش دانشجو در دانشگاه‌ها ، مدیریت شبکه‌های کامپیوتری، اقتصاد، زیست‌شناسی و پایداری جوامع میکروبی و…..

۱. سیستم پذیرش دانشگاه‌ها و دانشجویان

همان‌طور که اشاره کردیم، موضوع اصلی مقاله‌ی گیل و شاپلی در واقع اختصاص بهینه‌ی دانشجو به دانشگاه‌ها بود. در دهه‌ی ۱۹۶۰ و ۱۹۷۰، سیستم پذیرش دانشجو دچار مشکلات جدی بود. الگوریتم‌های سنتی مچینگ دانشجو و دانشگاه فقط در مقیاس‌های کوچک کارآمد بودند، اما زمانی که تعداد دانشجویان زیاد می‌شد، فرآیند پذیرش پیچیده و سردرگم‌کننده می‌شد. برای مثال، تصور کنید یک دانشکده در هر ترم مجبور بود تقاضای ۵۰۰ دانشجو را بررسی کند، در حالی که فقط ۵۰ نفر را می‌توانست بپذیرد. این فرآیند نه‌تنها برای دانشجویان، بلکه برای دانشگاه‌ها نیز چالش‌برانگیز بود.

راه‌حل گیل و شاپلی؛ الگوریتم آن‌ها باعث شد که فرآیند تخصیص دانشجو به دانشگاه‌ها به‌صورت خودکار و بهینه انجام شود. در این روش، دانشجویان بر اساس اولویت‌هایشان دانشگاه‌ها را انتخاب می‌کنند و دانشگاه‌ها نیز بر اساس اولویت‌های خود دانشجویان را پذیرش می‌کنند. در نهایت، این فرآیند به شکلی پیش می‌رود که همه‌ی پذیرش‌ها پایدار باشند و هیچ دانشجویی دانشگاهی را که به او پیشنهاد نداده ترجیح ندهد.

جالب است بدانید که سیستم پذیرش دانشجو در ایران نیز بر اساس همین الگوریتم کار می‌کند! زمانی که دانش‌آموزان انتخاب رشته می‌کنند، سامانه‌ی سازمان سنجش با استفاده از همین روش، دانشجویان را به دانشگاه‌های مختلف اختصاص می‌دهد.

۲. مدیریت شبکه‌های کامپیوتری (کلاینت و سرور)

حالا بیایید به دنیای کامپیوتر و اینترنت سر بزنیم. شاید فکر کنید این الگوریتم فقط در مسائل انسانی به کار می‌رود، اما واقعیت این است که یکی از مهم‌ترین کاربردهای آن در مدیریت شبکه‌ها و ارتباطات دیجیتالی است.

فرض کنید شما یک سرور هستید!
سرور در دنیای کامپیوتر، یک کامپیوتر مرکزی است که به درخواست‌های کاربران پاسخ می‌دهد. حالا تصور کنید که سه کاربر هم‌زمان به شما درخواست‌هایی ارسال می‌کنند:

• کاربر اول: می‌خواهد یک ایمیل ارسال کند.
• کاربر دوم: در حال تماشای یک مسابقه‌ی فوتبال به‌صورت آنلاین است.
• کاربر سوم: در حال مکالمه‌ی ویدیویی با دوستش است.

سؤال مهم این است که کدام درخواست باید اول پردازش شود؟ شما به‌عنوان یک سرور، نمی‌توانید به‌صورت هم‌زمان به همه‌ی درخواست‌ها پاسخ دهید، بنابراین باید آن‌ها را بر اساس اولویت پردازش کنید.

الگوریتم اولویت‌بندی سرور: سرور درخواست‌ها را بر اساس میزان اهمیت و حساسیت زمانی آن‌ها مرتب می‌کند:

• مکالمه‌ی تصویری: بالاترین اولویت را دارد، چون اگر بسته‌های داده با تاخیر ارسال شوند، کیفیت تماس کاهش پیدا می‌کند و کاربران تجربه‌ی بدی خواهند داشت.
• تماشای مسابقه‌ی فوتبال: اولویت کمتری دارد، چون چند میلی‌ثانیه تاخیر ممکن است مشکل بزرگی ایجاد نکند.
• ارسال ایمیل: کمترین حساسیت زمانی را دارد، زیرا اگر چند ثانیه دیرتر فرستاده شود، معمولاً مشکلی به وجود نمی‌آید.

در نتیجه، سرور ابتدا درخواست کاربر سوم را پردازش می‌کند، سپس درخواست کاربر دوم را انجام می‌دهد، و در نهایت، ایمیل کاربر اول را ارسال می‌کند.

۳. اقتصاد و تخصیص پایدار منابع

اقتصاد، علمی است که به تخصیص منابع محدود به افراد نیازمند می‌پردازد. از همین تعریف ساده می‌توان فهمید که مسئله ازدواج پایدار می‌تواند در اقتصاد نقش کلیدی داشته باشد. جالب است بدانید که جایزه نوبل اقتصاد در سال ۲۰۱۲ به طور مشترک به لوید شاپلی و الوین روث برای تحقیقاتشان در زمینه‌ی "تخصیص پایدار و طراحی بازار" اهدا شد.

در اکثر بازارهای اقتصادی، تعادل بین عرضه و تقاضا با مفهوم قیمت (پول) سنجیده می‌شود. اما برخی از بازارها چنان دارای محدودیت‌های اخلاقی و قانونی هستند که نمی‌توان معاملات را تنها بر اساس پول انجام داد. یکی از بارزترین مثال‌ها بازار پیوند عضو، به‌ویژه تبادل کلیه است.

• فرض کنید بیمار ۱ نیازمند کلیه است، و شخص ۲ داوطلب اهدای کلیه به اوست، اما کلیه‌ی شخص ۲ با بدن بیمار ۱ سازگار نیست.
• از طرف دیگر، بیمار ۳ نیازمند کلیه است، و شخص ۴ قصد دارد کلیه‌اش را به او اهدا کند، اما تطابق وجود ندارد.
• اما اگر کلیه‌ی شخص ۲ با بیمار ۳ سازگار باشد و کلیه‌ی شخص ۴ با بیمار ۱، می‌توان این جابجایی را انجام داد و دو زندگی را نجات داد.

این همان مفهوم "پایداری" در پیوند عضو است که شباهت زیادی به مسئله ازدواج پایدار دارد و امروزه در بسیاری از برنامه‌های تطبیق اهدای عضو از آن استفاده می‌شود.

۴. کاریابی و مچینگ کارفرما و کارجو

در بازار کار، ارتباط میان کارفرماها و کارجویان دقیقاً مشابه مسئله‌ی ازدواج پایدار است. کارفرماها لیستی از اولویت‌های خود برای جذب نیرو دارند و کارجویان نیز اولویت‌هایی برای انتخاب شغل مناسب. یک مثال جالب از این کاربرد در چین اتفاق افتاد. در سال ۲۰۱۶، به دلیل سیاست‌های جدید فرزندآوری، تقاضا برای پرستار بچه ۴۷٪ افزایش یافت.
"لویین وانگ" با استفاده از الگوریتم گیل-شاپلی، پلتفرم ORSB را طراحی کرد که خانواده‌ها و پرستاران کودک را به شیوه‌ای بهینه و پایدار به یکدیگر متصل کند. این پلتفرم روند استخدام را آسان‌تر و مطمئن‌تر کرد.

امروزه بسیاری از سایت‌های کاریابی آنلاین نیز از این الگوریتم برای تطبیق بهترین کارجویان با بهترین فرصت‌های شغلی استفاده می‌کنند.

۵. فیزیک و مکانیک آماری

این الگوریتم حتی در فیزیک و مدل‌های پیچیده‌ی مکانیک آماری هم وارد شده است.

در مکانیک آماری، یکی از موضوعات مهم، بررسی پایداری سیستم‌های فیزیکی در شرایط اولیه‌ی مختلف است. الگوریتم گیل-شاپلی می‌تواند برای حل مسائل بهینه‌سازی انرژی در سیستم‌های فیزیکی استفاده شود، جایی که هر ذره تمایل دارد در حالت بهینه‌ی خود قرار بگیرد، درست مانند جفت شدن پایدار در مسئله ازدواج پایدار.

۶. حل جدول سودوکو

حتی حل پازل‌هایی مثل سودوکو می‌تواند با الهام از مسئله‌ی ازدواج پایدار انجام شود!

مقاله‌ای با عنوان "The Stable Matching Problem & Sudoku" نشان داده که می‌توان نوع جدیدی از سودوکو را با این الگوریتم حل کرد، به این صورت که هر عدد در جدول به عنوان یک زوج احتمالی در نظر گرفته شود و مسئله را مانند یک مچینگ پایدار بررسی کرد.

۷. زیست‌شناسی و پایداری جوامع میکروبی

حتی جوامع میکروبی نیز می‌توانند از مدل ازدواج پایدار برای توضیح نحوه‌ی تعامل گونه‌های مختلف در یک اکوسیستم استفاده کنند.

جوامع میکروبی از هزاران گونه‌ی مختلف از باکتری‌ها و میکروارگانیسم‌ها تشکیل شده‌اند. هر گونه‌ی میکروبی، اولویت‌های غذایی خاص خود را دارد و وقتی منابع غذایی در محیط تغییر می‌کنند، باکتری‌ها ابتدا غذای مورد علاقه‌شان را مصرف می‌کنند و سپس به گزینه‌های بعدی می‌روند.

این فرایند مشابه مدل‌سازی پایداری در ازدواج پایدار است، جایی که هر میکروب یک انتخاب بهینه دارد و تعاملات آن با سایر میکروب‌ها یک مجموعه‌ی پایدار ایجاد می‌کند.

۸. آموزش ریاضی در مدارس

یک کاربرد جالب دیگر از این الگوریتم در آموزش ریاضی دبیرستان است.

در یک پایان‌نامه‌ی منتشر شده در سال ۲۰۱۵ با عنوان "The Stable Marriage Problem & Its Application In The High School Classroom"، اشاره شده که آموزش الگوریتم گیل-شاپلی در کلاس‌های درس می‌تواند انگیزه‌ی دانش‌آموزان را برای یادگیری نظریه گراف و طراحی الگوریتم افزایش دهد. از آنجایی که بسیاری از دانش‌آموزان دبیرستانی به روابط عاطفی علاقه‌مند هستند، استفاده از این مسئله می‌تواند روشی جذاب برای تدریس ریاضیات باشد!

می‌توان در پایان گفت الگوریتمی که دنیا را تغییر داد:

الگوریتم گیل-شاپلی بود؛ در نگاه اول ممکن است یک مسئله‌ی ساده‌ی ریاضی به نظر برسد، اما همان‌طور که دیدیم، کاربردهای گسترده‌ای در دنیای واقعی دارد. از پذیرش دانشجو و کاریابی گرفته تا مدیریت شبکه‌های کامپیوتری، بهینه‌سازی در فیزیک، مدل‌سازی جوامع میکروبی و حتی آموزش ریاضیات، این الگوریتم یکی از پرمصرف‌ترین و پرکاربردترین الگوریتم‌های ریاضی در دنیای مدرن است.

دفعه‌ی بعد که به پذیرش دانشگاه، یافتن شغل، یا حتی حل سودوکو فکر کردید، به یاد بیاورید که در پشت صحنه‌ی این فرآیندها، یک الگوریتم ریاضی هوشمند در حال کار است!