One-Class SVM for Anomaly Detection

در این مقاله به موضوع تشخیص ناهنجاری ها (Anomaly Detection) بوسیله الگوریتم One-Class SVM میپردازیم و مدل بهینه سازی این الگوریتم را در قالب ریاضیات و همچنین کتابخانه های زبان Python بررسی خواهیم کرد.

فهرست مطالب

- تعریف ناهنجاری

- تعریف الگوریتم SVM و مدل بهینه سازی آن

• توابع Kernel
• حاشیه (Margin) و Support Vector

- تعریف الگوریتم One-Class SVM و مدل بهینه سازی آن

- مقایسه الگوریتم های SVM و One-Class SVM

- تشخیص ناهنجاری با استفاده از تکنیک های Outlier Detection و Novelty Detection

- مزایا و معایب الگوریتم One-Class SVM

تعریف ناهنجاری

ناهنجاری به داده‌هایی اطلاق می‌شود که به طور قابل‌توجهی از رفتار یا الگوی کلی داده‌های عادی فاصله دارند. به عنوان مثال، تراکنش بانکی غیرعادی در یک حساب معمولاً به عنوان یک ناهنجاری شناسایی می‌شود. چنین داده‌هایی ممکن است نشان‌دهنده خطاهای سیستمی، رفتارهای غیرمعمول یا وقایع استثنایی باشند. شناسایی ناهنجاری‌ها در حوزه‌هایی مانند امنیت سایبری، تشخیص تقلب در تراکنش‌های مالی، و شناسایی بیماری‌های پزشکی اهمیت بسزایی دارد.

تعریف الگوریتم SVM و مدل بهینه‌سازی آن

ماشین بردار پشتیبان (SVM) یک الگوریتم یادگیری نظارت‌شده است که برای دسته‌بندی و رگرسیون مورد استفاده قرار می‌گیرد. هدف این الگوریتم یافتن یک ابرصفحه بهینه است که بتواند داده‌ها را به بهترین شکل ممکن تفکیک کند. این ابرصفحه باید حداکثر حاشیه ممکن بین نمونه‌های هر کلاس را تضمین کند، به گونه‌ای که داده‌ها با فاصله‌ای مناسب از این صفحه قرار گیرند.

همانطور که در شکل مشخص است اندازه تابع برای ابر صفحه برابر صفر است و برای هر یک از کلاس های سمت چپ و راست تابع مقدار 1- و 1+ را در نظر میگیریم؛ همچنین میدانیم که بردار W در تابع ابرصفحه همان بردار نرمال است.

حاشیه (Margin) و Support Vector

-حاشیه (Margin): فاصله بین ابرصفحه تصمیم‌گیری و نزدیک‌ترین نمونه‌های هر کلاس است. SVM تلاش می‌کند این حاشیه را بیشینه کند تا جداسازی دقیق‌تری انجام شود. در این قسمت یک مفهوم دیگری به اسم Soft Margin نیز وجود دارد که به سیستم امکان خطا و نادیده گرفتن داده های نویز را میدهد تا در نهایت پیش بینی و عملکرد بهتری داشته باشیم و ابر صفحه بهینه تری را رسم کند، برای این منظور از متغیر کمکی Slack استفاده میکنیم.

- بردار پشتیبان (Support Vector): نمونه‌هایی هستند که در مرز حاشیه قرار دارند و تعیین‌کننده موقعیت ابرصفحه هستند.

توابع Kernel

توابع کرنل ابزارهایی هستند که SVM را قادر می‌سازند تا در فضاهای غیرخطی نیز به خوبی عمل کند. این توابع ضرب داخلی داده‌ها را در یک فضای ویژگی بالاتر محاسبه می‌کنند تا امکان ایجاد مرزهای تصمیم‌گیری پیچیده‌تر فراهم شود. کرنل‌های متداول عبارت‌اند از:

- کرنل خطی: مناسب برای داده‌های قابل تفکیک خطی.

- کرنل چندجمله‌ای: برای داده‌های با روابط غیرخطی کاربرد دارد.

- کرنل گاوسی (RBF): برای داده‌های پیچیده با الگوهای غیرخطی مناسب است.

- کرنل سیگموید: در برخی از کاربردهای خاص، مانند شبکه‌های عصبی، استفاده می‌شود.

تعریف الگوریتم One-Class SVM و مدل بهینه‌سازی آن

الگوریتم One-Class SVM برای شناسایی ناهنجاری‌ها یا نمونه‌های جدید است. این الگوریتم با استفاده از داده‌های نرمال، یک مرز تصمیم‌گیری یا ابرصفحه ایجاد می‌کند که داده‌های نرمال را از داده‌های غیرمعمول جدا می‌کند. برای مثال، این الگوریتم می‌تواند در شناسایی تراکنش‌های غیرعادی در بانکداری یا تشخیص حملات سایبری مورد استفاده قرار گیرد.

تفاوت در مدل بهینه‌سازی

مدل بهینه‌سازی در One-Class SVM به گونه‌ای طراحی شده که:

- مرز تصمیم‌گیری را به گونه‌ای تعیین کند که داده‌های نرمال در سمت درستی از ابرصفحه قرار گیرند.

- اثر داده‌های غیرنرمال یا نقاط پرت را به حداقل برساند.

یکی از تفاوت‌های کلیدی، وزن‌دهی متفاوت مجموع اسلک‌ها (Slack Variables) است که حساسیت مدل به ناهنجاری‌ها را تنظیم می‌کند. همچنین، پارامتر p که نشان‌دهنده افست ابرصفحه از مبدأ است، نقش مهمی در تعیین موقعیت مرز تصمیم‌گیری ایفا می‌کند.

مقایسه الگوریتم‌های SVM و One-Class SVM

- هدف:

• الگوریتم SVM برای دسته‌بندی داده‌ها بین چندین کلاس طراحی شده است.
• الگوریتم One-Class SVM برای شناسایی داده‌های غیرمعمول یا نمونه‌های ناشناخته کاربرد دارد.

- داده‌های ورودی:

• الگوریتم SVM نیاز به داده‌های برچسب‌دار از تمام کلاس‌ها دارد.
• الگوریتم One-Class SVM تنها از داده‌های نرمال برای آموزش استفاده می‌کند.

- حاشیه (Margin):

• در SVM برای جدا کردن کلاس‌ها تعریف می‌شود.
• در One-Class SVM برای جدا کردن داده‌های نرمال از داده‌های ناهنجار استفاده می‌شود.

تشخیص ناهنجاری با استفاده از تکنیک‌های Outlier Detection و Novelty Detection

تکنیک Outlier Detection:

این تکنیک به شناسایی نقاطی می‌پردازد که از الگوی کلی داده‌های مشاهده‌شده فاصله دارند. معمولاً در تحلیل داده‌های موجود به کار می‌رود.

کد Python

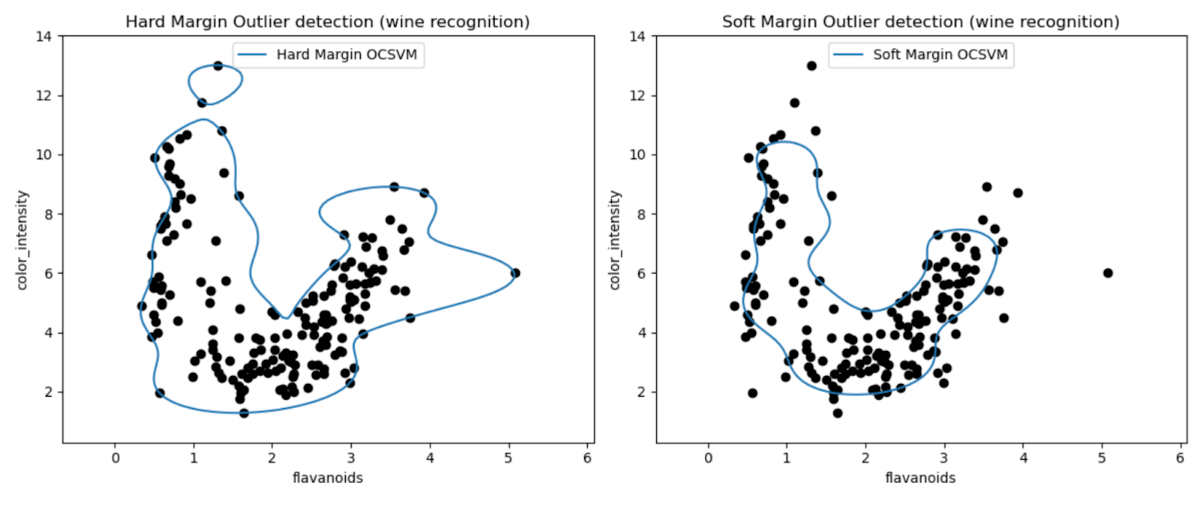
این نمودارها به ما امکان می‌دهند عملکرد مدل‌های One-Class SVM را در تشخیص داده‌های غیرعادی (Outliers) در مجموعه داده Wine به صورت بصری بررسی کنیم.

با مقایسه نتایج مدل‌های One-Class SVM با حاشیه سخت و نرم، می‌توان مشاهده کرد که انتخاب تنظیمات حاشیه (پارامتر nu) چگونه بر تشخیص داده‌های غیرعادی تأثیر می‌گذارد.

مدل حاشیه سخت با مقدار بسیار کوچک برای پارامتر nu (مانند 0.01) احتمالاً منجر به ایجاد یک مرز تصمیم‌گیری محافظه‌کارانه‌تر می‌شود. این مدل به گونه‌ای عمل می‌کند که به‌طور محکم دور اکثر نقاط داده پیچیده و احتمالاً تعداد کمتری از نقاط را به‌عنوان داده غیرعادی طبقه‌بندی می‌کند.

از سوی دیگر، مدل حاشیه نرم با مقدار بزرگ‌تر برای پارامتر nu (مانند 0.35) احتمالاً مرز تصمیم‌گیری انعطاف‌پذیرتری ایجاد می‌کند. این امر باعث می‌شود حاشیه وسیع‌تری تعریف شده و تعداد بیشتری از داده‌های غیرعادی شناسایی شوند.

تکنیک Novelty Detection:

این روش بر شناسایی نمونه‌های جدید و ناشناخته‌ای تمرکز دارد که در داده‌های آموزشی دیده نشده‌اند. این تکنیک برای محیط‌های پویا و داده‌های متغیر مناسب است.

کد Python

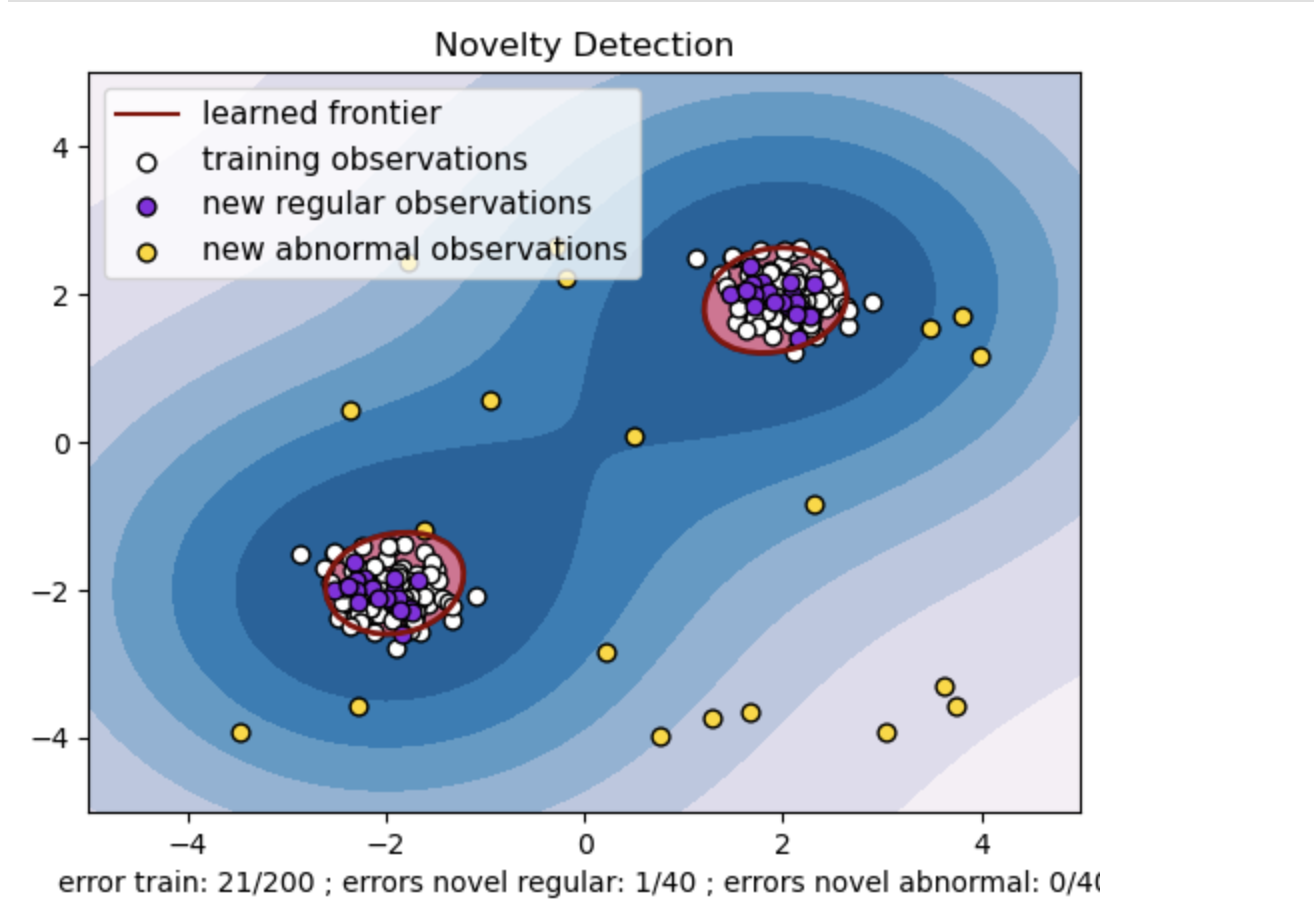
یک مجموعه داده مصنوعی با دو خوشه از نقاط داده تولید کنید. این کار را با استفاده از توزیع نرمال در اطراف دو مرکز متفاوت: (2, 2) و (2-, 2-) برای داده‌های آموزشی و آزمایشی انجام دهید. بیست نقطه داده را به صورت تصادفی در یک ناحیه مربعی از 4- تا 4 در هر دو بعد تولید کنید. این نقاط داده، مشاهدات غیرعادی یا Outliers را نشان می‌دهند که به طور قابل توجهی از رفتار معمول مشاهده شده در داده‌های آموزشی و آزمایشی انحراف دارند.

مرز یادگیری‌شده به مرز تصمیم‌گیری‌ای اشاره دارد که مدل One-Class SVM یاد گرفته است. این مرز، نواحی فضای ویژگی را که مدل نقاط داده را به‌عنوان نرمال در نظر می‌گیرد، از نقاط غیرعادی جدا می‌کند.

تغییر رنگ از آبی به سفید در خطوط هم‌تراز (Contours) نشان‌دهنده درجات مختلف اطمینان یا قطعیت مدل One-Class SVM در نواحی مختلف فضای ویژگی است. سایه‌های تیره‌تر نشان‌دهنده اطمینان بیشتر مدل در طبقه‌بندی نقاط داده به‌عنوان «نرمال» هستند. آبی تیره، نواحی‌ای را نشان می‌دهد که مدل با اطمینان قوی به‌عنوان «نرمال» طبقه‌بندی می‌کند. با روشن‌تر شدن رنگ در خطوط هم‌تراز، مدل در طبقه‌بندی نقاط داده به‌عنوان «نرمال» کمتر مطمئن است.

این نمودار به صورت بصری نشان می‌دهد که چگونه مدل One-Class SVM می‌تواند بین مشاهدات معمولی و غیرعادی تمایز قائل شود. مرز تصمیم‌گیری یادگیری‌شده، نواحی مشاهدات نرمال و غیرعادی را از یکدیگر جدا می‌کند. مدل One-Class SVM برای شناسایی مشاهدات غیرعادی در یک مجموعه داده اثربخشی خود را ثابت می‌کند.

حال اگر مقدار ابرپارامتر nu را برابر با 0.5 قرار دهیم نمودار به این شکل خواهد بود:

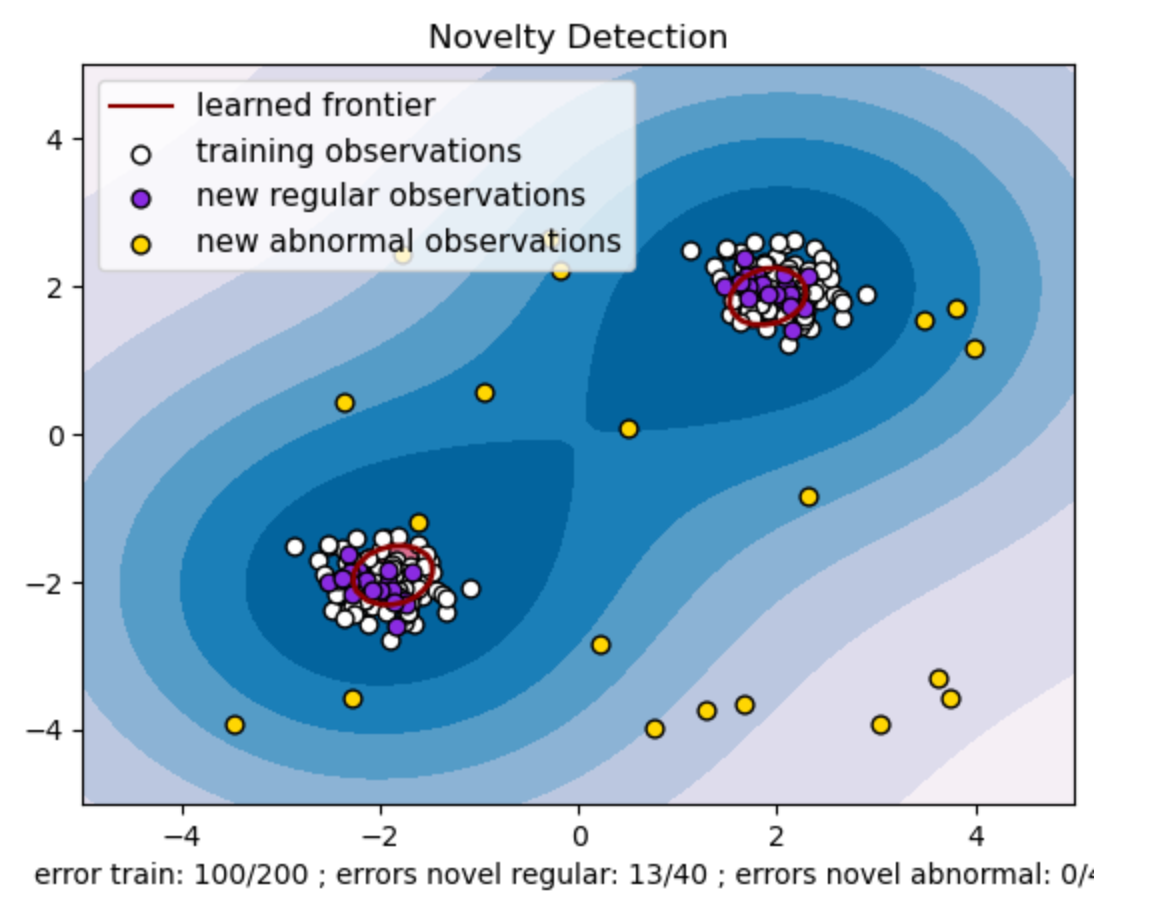
مقدار "nu" در مدل One-Class SVM نقش بسیار مهمی در کنترل درصد داده‌های غیرعادی (Outliers) که توسط مدل قابل تحمل است، ایفا می‌کند. این مقدار مستقیماً بر توانایی مدل در شناسایی داده‌های غیرعادی تأثیر می‌گذارد و پیش‌بینی‌های مدل را تحت تأثیر قرار می‌دهد.

می‌توان مشاهده کرد که مدل اجازه می‌دهد 100 نقطه آموزشی به اشتباه طبقه‌بندی شوند. مقدار پایین‌تر برای "nu" به معنای محدودیت سخت‌گیرانه‌تر در درصد داده‌های غیرعادی قابل قبول است.

انتخاب مقدار مناسب برای "nu" عملکرد مدل را در شناسایی داده‌های غیرعادی تحت تأثیر قرار می‌دهد و نیازمند تنظیم دقیق با توجه به نیازهای خاص کاربرد و ویژگی‌های مجموعه داده است.

حال اگر در همین نمودار مقدار ابرپارامتر gamma را هم برابر با 0.5 قرار دهیم، به این شکل خواهیم رسید:

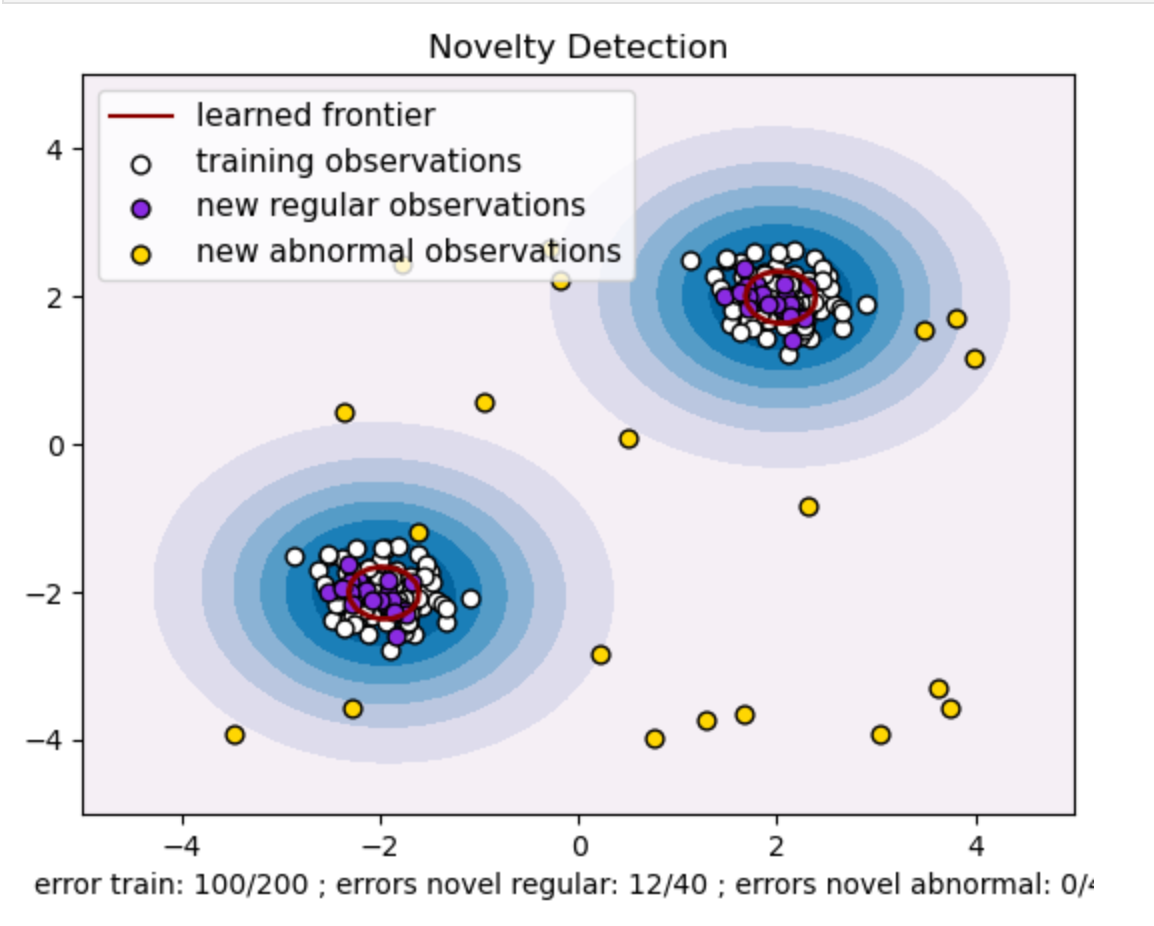
در مدل One-Class SVM، ابرپارامتر gamma نمایانگر ضریب کرنل برای کرنل RBF است. این ابرپارامتر شکل مرز تصمیم‌گیری را تحت تأثیر قرار می‌دهد و در نتیجه، بر عملکرد پیش‌بینی مدل تأثیر می‌گذارد.

زمانی که مقدار gamma بالا باشد، هر نمونه آموزشی تنها بر محدوده نزدیک به خود تأثیر می‌گذارد. این امر باعث ایجاد مرز تصمیم‌گیری محلی‌تر می‌شود. بنابراین، نقاط داده باید به بردارهای پشتیبان نزدیک‌تر باشند تا به همان کلاس تعلق داشته باشند.

مزایا و معایب One-Class SVM

مزایا

1. توانایی یادگیری از داده‌های بدون برچسب ناهنجاری.
2. انعطاف‌پذیری بالا با استفاده از توابع کرنل برای داده‌های غیرخطی.
3. عملکرد مناسب در شناسایی الگوهای نادر و نقاط غیرمعمول.

معایب

1. حساسیت بالا به انتخاب پارامترها، مانند نوع کرنل و مقادیر مربوط به اسلک، که ممکن است به تنظیمات دقیقی نیاز داشته باشد.
2. نیاز به تنظیم مدل برای دستیابی به عملکرد بهینه.
3. پیچیدگی محاسباتی بالا، خصوصاً در مجموعه داده‌های بزرگ.

جمع بندی

استفاده از One-Class SVM برای تشخیص داده‌های غیرعادی و شناسایی نوآوری (Novelty Detection) یک راه‌حل قدرتمند در حوزه‌های مختلف ارائه می‌دهد. این روش در سناریوهایی که داده‌های غیرعادی برچسب‌دار کم یا در دسترس نیستند، بسیار مفید است. بنابراین، در کاربردهای واقعی که داده‌های غیرعادی نادر هستند و تعریف صریح آن‌ها دشوار است، ارزش ویژه‌ای دارد.

موارد استفاده از این روش به حوزه‌های متنوعی مانند امنیت سایبری و تشخیص خطا گسترش می‌یابد، جایی که داده‌های غیرعادی می‌توانند پیامدهای مهمی داشته باشند. با این حال، در حالی که One-Class SVM مزایای زیادی ارائه می‌دهد، لازم است ابرپارامترهای آن متناسب با داده‌ها تنظیم شوند تا نتایج بهتری حاصل شود، که این کار ممکن است گاهی اوقات وقت‌گیر باشد.