Principle Component Analysis (PCA) به زبان ساده

به عنوان یک شخصی که هدفش این هست که وارد دنیای علم داده بشه حتما از اولین چیزهایی که می‌شنوید روشی تحت عنوان PCA هست! مفهوم PCA معمولا سخت و پیچیده بیان می‌شه و خود من برای اینکه حس خوبی از فهمش داشته باشم به ویدئوهای زیادی رجوع کردم و سوالات زیادی در ذهنم به وجود اومد! توی این پست می‌خوام این مفهوم رو به ساده‌ترین شکل ممکن بیان کنم.

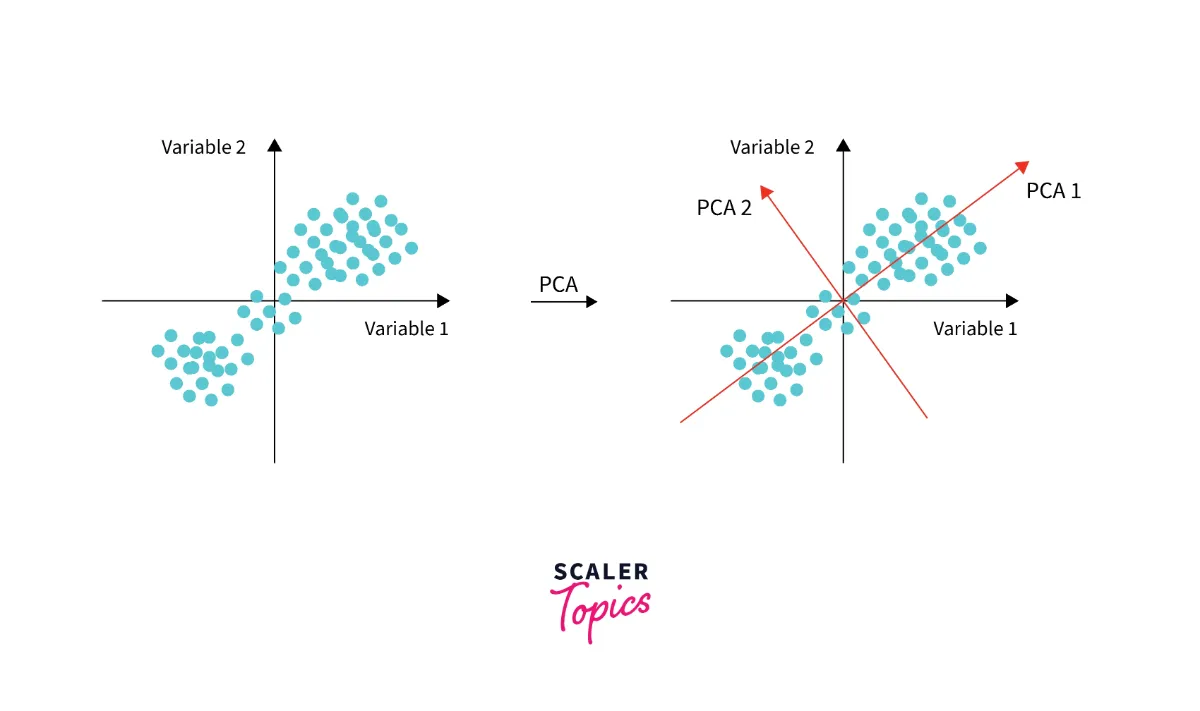
فرض کنید که شما یک مجموعه داده دارید از قد و وزن‌های دانش‌آموزان یک کلاس مثل شکل زیر:

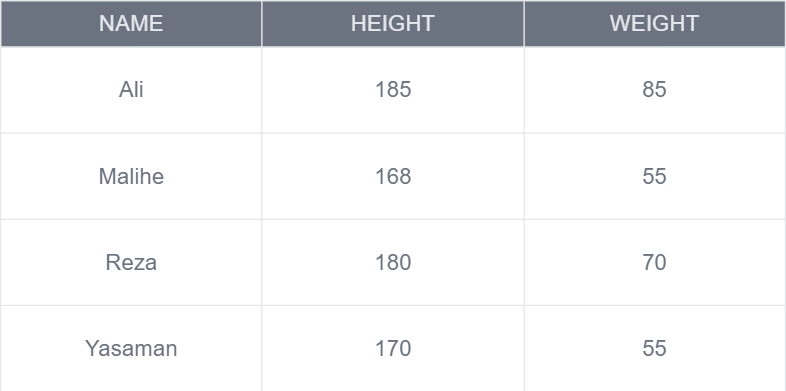
حالا فرض کنید که حافظه سیستم شما فقط به شما اجازه می‌ده که ۸ مقدار رو در اون ذخیره کنید. پس شما باید ۴ مقدار نام در اون ذخیره کنید و از بین ۴ مقدار قد و ۴ مقدار وزن مجبور می‌شید که تنها ۴ تای اون‌هارو نگه دارید!
اینجا مسئله ما به شکل زیر تعریف می‌شود:
چگونه ۴ مقدار ذخیره کنم که هم بتوانم اطلاعات مربوط به قد دانشجویان و هم اطلاعات مربوط به وزن دانشجویان رو ذخیره کنم؟
در این مسئله ما با استفاده از PCA می‌توانیم این دو مقدار را تبدیل به یک مقدار بکنیم و مسئله خود را حل کنیم.
چگونه؟

از منظر معنایی Principle Component به معنای جز اصلی است و در مثال ما کاری که می‌کند این هست که یک ویژگی جدید از مقادیر قد و وزن هر شخص تولید می‌کند که نمایانگر مقدار قد و وزن در یک ویژگی جدید هست!
کاربرد این PCها یا جزهای اصلی در دنیای علم داده در کجاست؟
هنگامی که ما داده‌های زیادی داریم، نیاز داریم که این داده‌ها را از نظر حجم کاهش دهیم تا بتوانیم داده‌ها را تحلیل کنیم و هم بتوانیم در مصرف حافظه صرف‌جویی کنیم. برای تحلیل داده‌ها ما از تصویرسازی اون‌ها استفاده می‌کنیم. مثل شکل زیر:

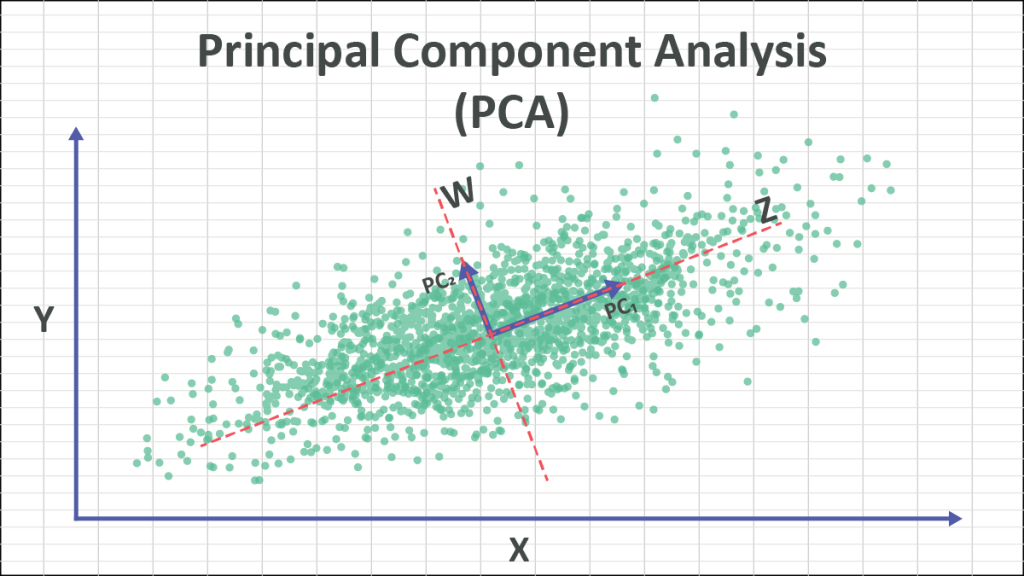
اگر که داده ما ۲ ویژگی داشته باشد مثل قد و وزن دانش‌آموزان، خب می‌توانیم در ۲ بعد X و Y همانند بالا نمایش دهیم و توزیع داده‌های خودمان را ببینیم. اما اگر داده‌های ما بیشتر از ۲ بعد باشند چه؟ مثلا فرض کنید می‌خواهیم یک مدل آموزش دهیم که وضعیت فیزیکی دانش‌آموزان را بسنجد. در این مدل ما علاوه بر قد و وزن نیازمند ویژگی‌های دیگری همچون سن، رنگ پوست، سلامت کبد، سلامت کلیه و ... را نیز داشته باشد تا بتواند پیش‌بینی دقیقی انجام دهد. اگر که ما بخواهیم این داده با فرضا ۳۰ ویژگی از دانش‌آموزان را تصویرسازی کنیم آیا ممکن است؟
طبیعتا ممکن نیست زیرا که ما نهایتا بتوانیم یک نمودار با ۳ بعد رسم کنیم. پس از تکنیک یا روش PCA استفاده می‌کنیم تا بتوانیم با حفظ بیشترین اطلاعات ابعاد داده خود را کاهش دهیم و بتوانیم به تصویری از داده خود برسیم تا روابط بین داده‌ها را پیدا کنیم.

اینجا سوالات زیادی به وجود میاد مثل اینکه ما داده‌هامون رو چجوری می‌تونیم از ۳۰ بعد به ۲ بعد ببریم؟‌ آیا این کار باعث از دست رفتن اطلاعات متغیرهای دیگه نمی‌شه؟ چگونه اصلا چنین کاری ممکن هست؟ برای پاسخ به این سوالات لازم هست که به صورت ریاضی وارد تحلیل نحوه عملکرد PCA بشیم که هدف این پست نیست. مطالب خوبی در سطح اینترنت به بیان خوب اون‌ها پرداختند. در صورتی که مشتاق بودید برای اون موارد هم می‌توانم پستی درست کنم. (در کامنت‌ها اعلام کنید.)

در زیر به بیان گام‌هایی که در تکنیک Principle Component Analysis یا تحلیل جزهای اصلی طی می‌کنیم را به صورت خلاصه توضیح می‌دهم تا نقشه راهی از مفاهیمی که برای درک مفهوم PCA نیاز هست به شما عزیزان داده شود.
۱- داده‌ها را روی مرکز نمودار قرار دهیم.

چرا داده‌های خودمان را مرکز کنیم و چطوری؟
ما داده‌های خودمون رو به مرکز نمودار می‌آوریم زیرا که می‌خواهیم در ادامه محاسباتی انجام دهیم که این مرکز بودن داده آن‌ها رو راحت‌تر خواهد کرد. (در همین حد برای مفهوم بدونید بس هست)
اگر هر داده رو از میانگین خودش کم کنید روی مرکز نمودار توزیع می‌شود. به عنوان مثال در مثال قد و وزن دانش‌آموزان میانگین قد تقریبا ۱۷۵ بود پس اگر مقادیر قد رو ۱۷۵ تا ازش کم کنیم و میانگین وزن که تقریبا ۶۶ هست رو از مقادیر وزنی کم کنیم داده ما حول مرکز قرار می‌گیرد.

۲- ماتریس کوواریانس را حساب کنیم.
ماتریس کوواریانس چیه؟ این ماتریس یک جدول هست که اطلاعاتی درباره نحوه توزیع‌شدگی داده‌ها و ارتباطات اون‌ها با یکدیگر به ما می‌دهد. (مثلا کوواریانس قد و وزن به این معناست که قد و وزن چه ارتباطی با یکدیگر دارند، آیا با رشد قد الزاما وزن هم زیاد می‌شود؟ مقدار کوواریانس دو ویژگی یک عدد اسکالر مثبت یا منفی می‌تواند باشد.)

۳- به دست‌آوردن مقدار بردار آیگن و مقدار آیگن ماتریس کوواریانس.
بردار آیگن یک بردار بر روی نمودار هست که ما مقادیر داده خودمون رو بر روی اون بازتاب می‌کنیم تا مقدار جدید رو به دست بیاریم. (بردار آیگن یک بردار با ویژگی‌های خوب برای ما هست که ما روش داده‌‌های قد و وزن خودمون رو بازتاب کنیم و یک ویژگی جدید درست کنیم!)

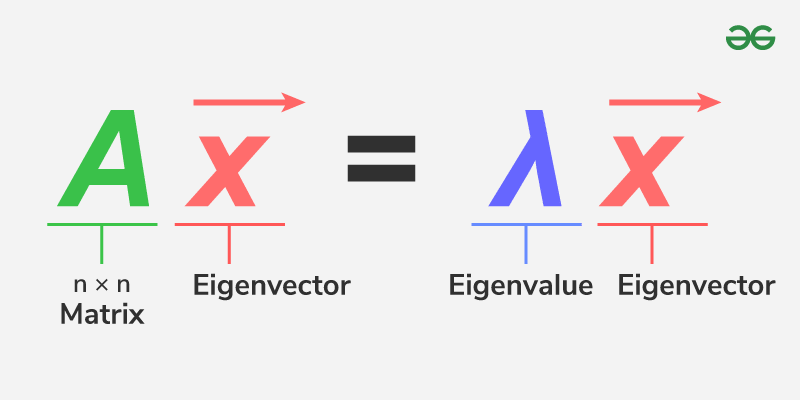
۴- داده‌های خودمون رو روی بردار آیگن بازتاب می‌دهیم. (که از حجم داده‌هایمان کم کنیم و بتوانیم داده‌هایمان را تحلیل کنیم.)

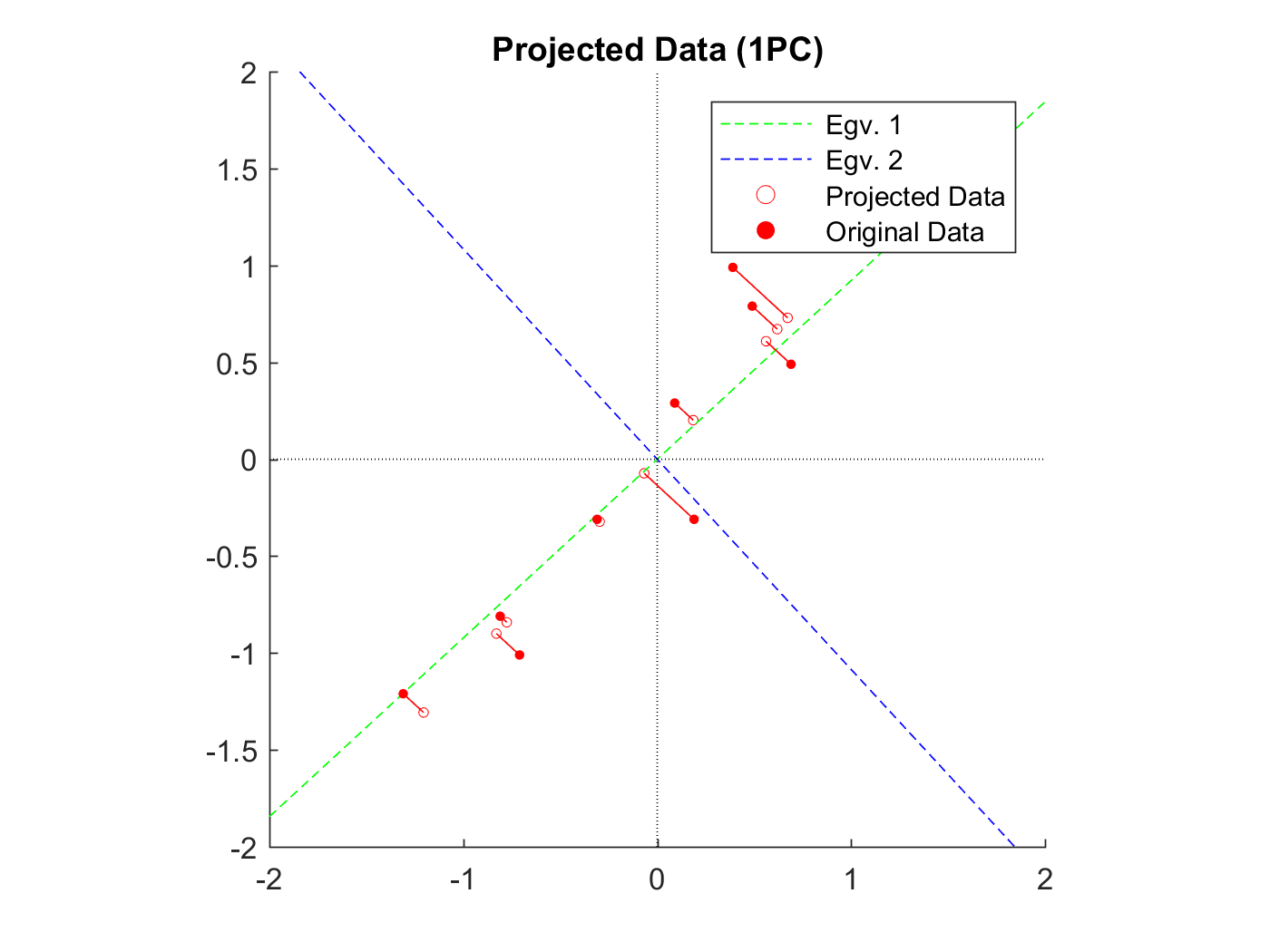
۵- مقادیری که روی بردار آیگن بازتاب داده شده‌اند یک مقدار به ازای چندین ویژگی را دارند.
در مثال قد و وزن دانش‌آموزان ما به یک مقدار به ازای ۲ ویژگی خودشون کاهش داده می‌شوند در حالی که همچنان با داشتن اون مقدار ما می‌توانیم نسبت قد و وزن اون‌ها رو به همدیگر متوجه شویم.

در این توضیحات مفاهیمی نام برده شد که توضیح داده نشده‌اند مثل بردار آیگن یا ماتریس کوواریانس در ویرگول مطالب خوبی با بیان جزئیات به بیان این مفاهیم پرداخته‌اند. هدف از این پست این هست که آشنایی کلی با PCA به کسانی که اولین بار با این مفهوم برخورد می‌کنند داده شود. همچنین با بیان گام‌های PCA برای کسانی که دنبال راهی برای به دست آوردن PCA هستند نقشه راهی به آن‌ها داده شود تا بدانند چه مفاهیمی را جست‌وجو کنند.

امیدوارم که مطلب براتون مفید بوده باشه. شاد و پیروز و موفق باشید.