یک تصویر کلی از شبکه‌ عصبی: بدون پیچیدگی، بدون ریاضی

مقدمه

در این مطلب قصد داریم یک مدل ذهنی ساده از نحوه‌ی عملکرد شبکه‌های عصبی و فرآیند train کردن آن‌ها ارائه دهیم. برای توضیح بهتر، از مثال تبدیل تصاویر اعداد دست‌نویس به عدد متناظر استفاده می‌کنیم. 

تمام مواردی که در ادامه مطرح می‌شود صرفاً برای ایجاد یک درک مفهومی و ذهنی از نحوه‌ی عملکرد شبکه‌های عصبی و فرآیند train کردن آن‌ها است — نه لزوماً همان چیزی که امروزه در دنیای واقعی و پیاده‌سازی‌های عملی مورد استفاده قرار می‌گیرد.

خواندن این مطلب نیاز به هیچ پیش‌نیازی ندارد.

نورون چیست؟

هر نورون در یک شبکه عصبی عددی بین صفر و یک را نگه می‌دارد که به آن activation گفته می‌شود. برای مثال، در پردازش تصویر، مقدار روشنایی یک پیکسل در یک تصویر سیاه‌ و سفید می‌تواند همان مقدار activation نورون در لایه‌ی ورودی باشد. در مسئله‌ی تشخیص اعداد از روی تصویر، لایه‌ی خروجی شبکه معمولاً شامل ۱۰ نورون است (برای اعداد ۰ تا ۹)، و مقدار فعال‌سازی هر نورون نشان‌دهنده‌ی شباهت تصویر ورودی به آن عدد است.

هدف شبکه عصبی چیست؟

هدف اصلی شبکه عصبی، یافتن روشی است که بتواند داده‌های خام (مانند پیکسل‌های تصویر) را به مفاهیم انتزاعی‌تر (مثل اشیاء یا اعداد) تبدیل کند.

به عنوان مثال، در مسئله‌ی تشخیص عدد از تصویر:

• لایه‌ی اول شبکه -مجموعه‌ای از نورون‌ها- از پیکسل‌های خام تشکیل شده است. یعنی هر پیکسل متناظر یک نورون است.

• لایه‌ی دوم یاد می‌گیرد از روی پیکسل‌ها، الگوهایی مانند لبه‌ها (edges) را استخراج کند.

• لایه‌های بعدی از ترکیب این لبه‌ها، الگوهای پیچیده‌تر (patterns) مثل خطوط و منحنی‌ها را شناسایی می‌کنند.

• در نهایت، لایه‌ی خروجی این الگوها را با مفاهیمی مانند عدد «8» یا «9» مطابقت می‌دهد.

وزن و بایاس (Weight & Bias):

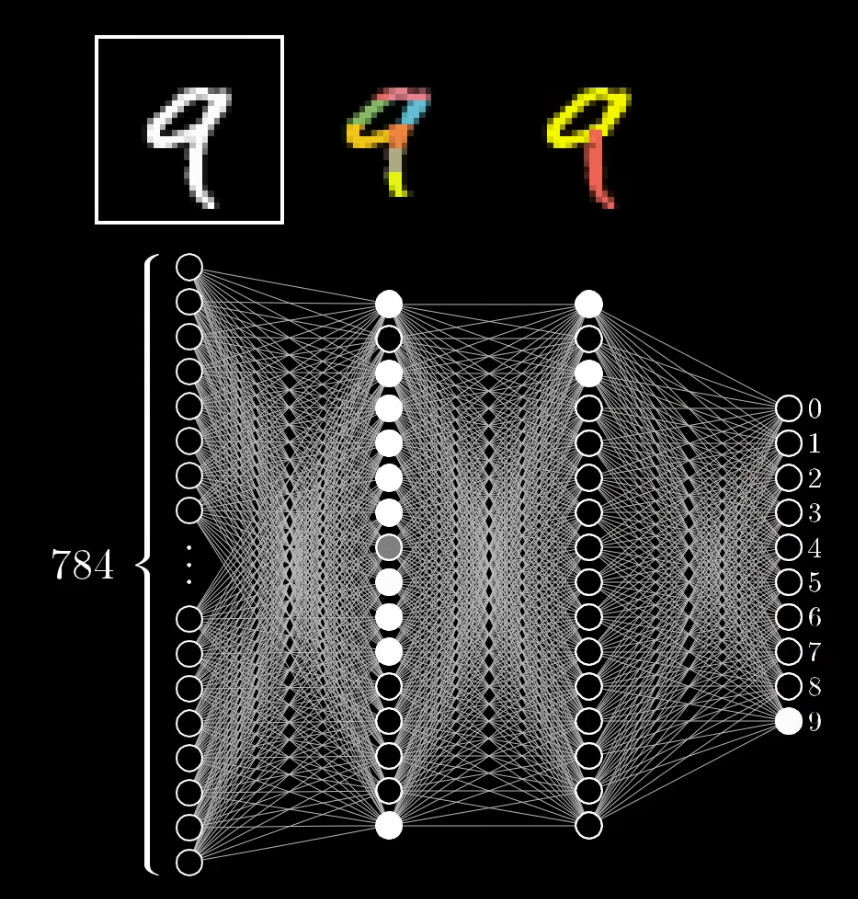
در شبکه عصبی، هر نورون از یک لایه به تمام نورون‌های لایه‌ی بعدی متصل است. هر اتصال دارای وزنی (Weight) است که مشخص می‌کند خروجی یک نورون تا چه حد بر فعال‌سازی نورون بعدی تأثیر بگذارد.

به عنوان مثال، اگر نورونی در لایه‌ی اول (مثلاً یک پیکسل روشن) فعال باشد، وزن‌ها تعیین می‌کنند که کدام نورون‌ها در لایه‌ی دوم (مثلاً نورون‌های شناسایی‌کننده‌ی لبه‌ها) فعال شوند.

برای افزایش دقت مدل، هر نورون علاوه بر وزن‌ها، یک بایاس (Bias) نیز دارد؛ مقداری ثابت که به مجموع ورودی‌ها اضافه می‌شود تا شبکه بتواند مرز تصمیم (decision boundary) را بهتر تنظیم کند و در نتیجه انعطاف‌پذیری بیشتری در یادگیری روابط پیچیده داشته باشد.

در نهایت، برای تبدیل مجموع وزن‌دار ورودی‌ها و بایاس به عددی بین صفر و یک، از تابع فعال‌سازی (Activation Function) مانند Sigmoid یا ReLU استفاده می‌شود.

حال این پرسش مطرح می‌شود که شبکه عصبی چگونه یاد می‌گیرد وزن‌ها و بایاس‌های خود را به‌گونه‌ای تنظیم کند که از مجموعه‌ای از داده‌های خام، به درک یک مفهوم (مثلاً تشخیص عدد در تصویر) برسد؟ در ادامه به پاسخ این سؤال می‌پردازیم.

فرض کرده‌ایم که مسئله‌ی ما تشخیص اعداد دست‌نویس از روی تصویر است. برای آموزش شبکه به یک دیتاست برچسب‌دار (Labeled Dataset) نیاز داریم؛ یعنی مجموعه‌ای از تصاویر اعداد دست‌نویس که عدد واقعیِ هر تصویر از قبل مشخص باشد. هدف این است که شبکه عصبی یاد بگیرد بین پیکسل‌های تصویر و عدد متناظر با آن رابطه برقرار کند.

در آغاز، وزن‌ها و بایاس‌ها معمولاً به‌صورت تصادفی مقداردهی می‌شوند، بنابراین خروجی اولیه‌ی شبکه بسیار نادرست و تصادفی است. در این مرحله، شبکه هیچ درکی از داده ندارد.

اینجاست که مفهوم تابع هزینه (Cost Function) وارد می‌شود.

تابع هزینه (Cost Function):

تابع هزینه مشخص می‌کند که خروجی فعلی شبکه چقدر با خروجی واقعی (مقدار صحیح) فاصله دارد. هر چه مقدار تابع هزینه بیشتر باشد، یعنی پیش‌بینی شبکه اشتباه‌تر بوده است.

به زبان ساده:

• اگر شبکه خروجی درستی بدهد (مثلاً تصویر عدد ۳ را درست تشخیص دهد)، مقدار تابع هزینه کم خواهد بود.

• اگر شبکه اشتباه کند (مثلاً عدد ۳ را به‌عنوان ۸ تشخیص دهد)، مقدار تابع هزینه زیاد می‌شود.

هدف آموزش شبکه عصبی این است که مقدار تابع هزینه را به حداقل برساند؛ یعنی وزن‌ها و بایاس‌ها طوری تنظیم شوند که پیش‌بینی شبکه تا حد ممکن به مقدار واقعی نزدیک شود.

پس از محاسبه هزینه برای همه داده‌های برچسب‌گذاری شده، از تمام خروجی‌های cost function میانگین گرفته می‌شود. این عدد نشان‌دهنده‌ی دقت کلی شبکه عصبی در پیش‌بینی داده‌هاست.

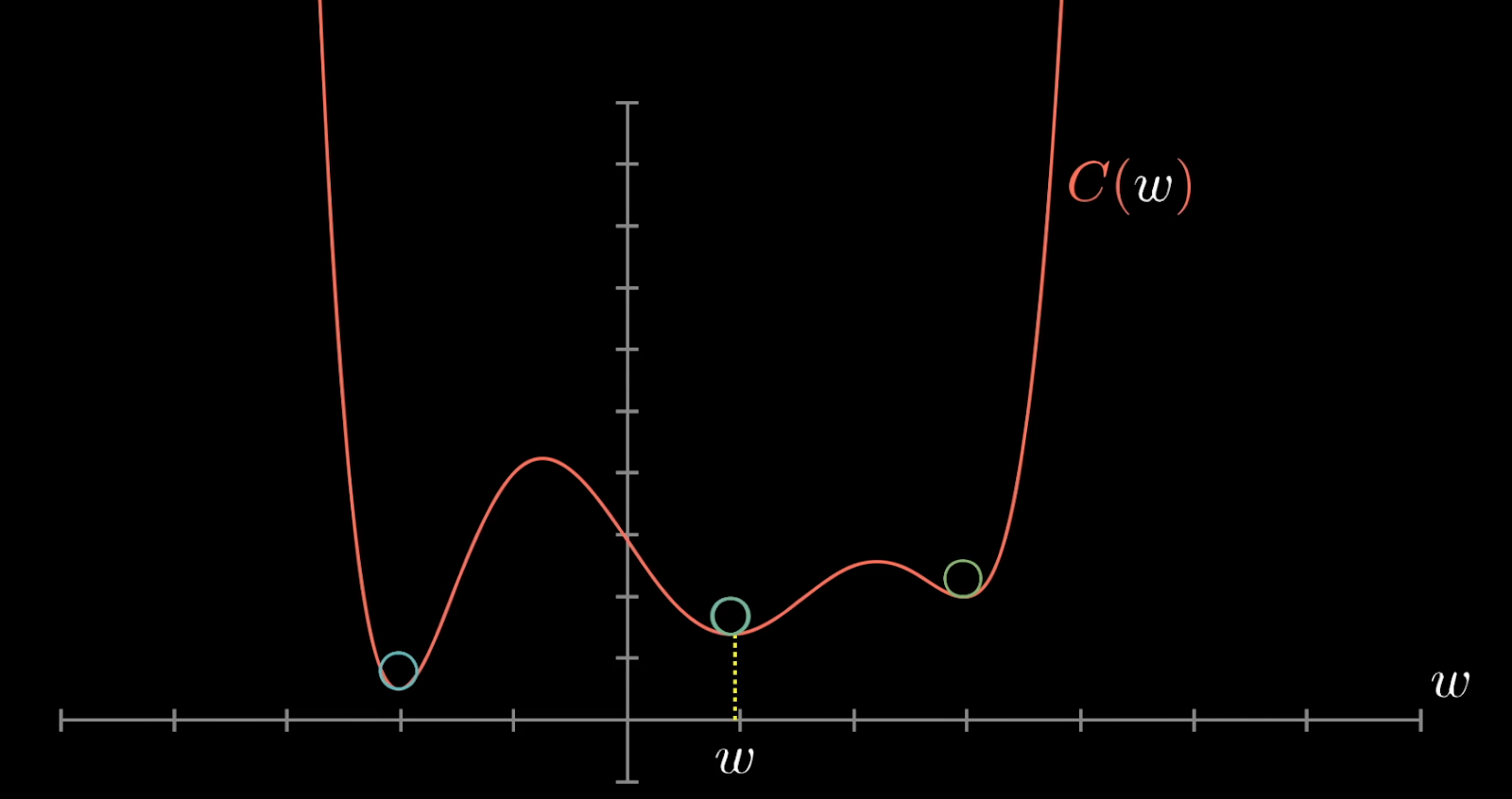
در این مرحله هدف ما این است که بفهمیم چطور می‌توان مقدار cost را کاهش داد. برای ساده‌سازی، می‌توان کل شبکه عصبی را مانند یک تابع ریاضی بزرگ در نظر گرفت که ورودی آن وزن‌ها و بایاس‌ها هستند و خروجی‌اش عددی است که توسط cost function محاسبه می‌شود. اگر این تابع را در یک فضای دوبعدی فرض کنیم، (در دنیای واقعی این یک مسئله n بعدی است که نمی‌توان آن را visualize کرد،) هدف ما پیدا کردن نقطه‌ی minimum این تابع است — یعنی جایی که مقدار cost کمترین مقدار ممکن باشد.

البته در عمل به دنبال local minimum هستیم، نه لزوماً global minimum، چون پیدا کردن کمینه‌ی کلی برای تابعی با میلیون‌ها پارامتر بسیار پیچیده است.

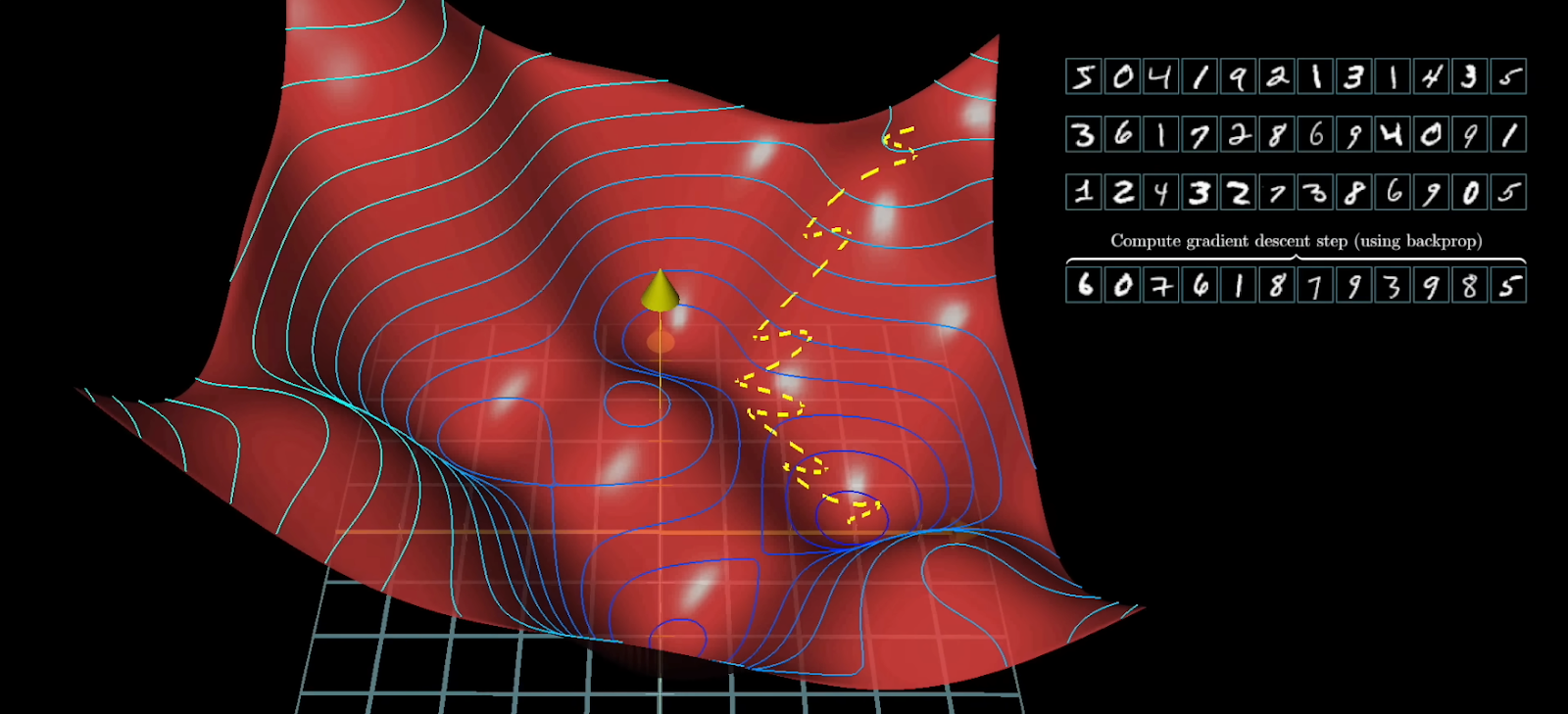
فرآیند ساده‌ی رسیدن به local minimum را می‌توان به شکل زیر خلاصه کرد:

1. با یک ترکیب تصادفی از وزن‌ها و بایاس‌ها شروع می‌کنیم.

2. مقدار cost را محاسبه می‌کنیم.

3. با استفاده از یک تابع ریاضی (مثل gradient)، وزن‌ها و بایاس‌ها را کمی تغییر می‌دهیم.

4. دوباره cost را محاسبه می‌کنیم:

   • اگر مقدار cost کم‌تر شد، در همان جهت ادامه می‌دهیم.

   • اگر مقدار cost زیاد شد، جهت تغییر را معکوس می‌کنیم.

5. این فرآیند بارها تکرار می‌شود تا زمانی که دیگر کاهش قابل توجهی در cost دیده نشود.

به این الگوریتم که مشخص می‌کند وزن‌ها و بایاس‌ها در هر مرحله چگونه تغییر کنند تا cost کاهش یابد، Backpropagation گفته می‌شود. در ادامه به نحوه‌ی عملکرد آن پرداخته خواهد شد.

Backpropagation چیست؟

برای درک بهتر، با یک مثال پیش برویم. فرض کنید تصویری از عدد ۲ داریم و آن را به شبکه عصبی می‌دهیم. خروجی شبکه مجموعه‌ای از activation‌ها در ۱۰ نورون لایه آخر است (هر نورون نماینده‌ی یکی از اعداد ۰ تا ۹ است).

در حالت ایده‌آل، می‌خواهیم نورون متناظر با عدد ۲ مقدار activation نزدیک به ۱ داشته باشد و سایر نورون‌ها به ۰ نزدیک باشند. اما در عمل، خروجی شبکه با این انتظار فاصله دارد — مثلاً نورون عدد ۳ نیز تا حدی فعال شده است.

حالا سؤال این است: چطور باید شبکه را طوری تنظیم کنیم که خروجی به هدف نزدیک‌تر شود؟

ما نمی‌توانیم مستقیماً activation نورون‌ها را تغییر دهیم؛ تنها چیزی که در کنترل ماست وزن‌ها (weights) و بایاس‌ها (biases) هستند.

ایده این است که وزن‌هایی که باعث افزایش activation نورون درست (عدد ۲) می‌شوند را افزایش دهیم و وزن‌هایی که به اشتباه نورون‌های دیگر را فعال کرده‌اند را کاهش دهیم. نورون‌هایی که در لایه قبل فعال‌تر بوده‌اند، تأثیر بیشتری در این تغییر دارند. پس وزن اتصالات (legs) بین نورون‌های فعال‌تر در لایه قبل و نورون هدف در لایه بعد باید بیشتر تنظیم شوند.

به صورت استعاری، این مفهوم با Hebbian theory در نوروسایکولوژی هم‌خوانی دارد که می‌گوید:

“Neurons that fire together, wire together.”

یعنی نورون‌هایی که با هم فعال می‌شوند، ارتباط قوی‌تری با هم شکل می‌دهند.

در Backpropagation، ما این فرایند را برای تمام خروجی‌ها (اعداد ۰ تا ۹) انجام می‌دهیم و اثر هرکدام را بر وزن‌های بین لایه‌ها لحاظ می‌کنیم.

در واقع وزن هر اتصال بین دو لایه، بر اساس میانگین تغییرات خطا (error gradients) برای تمام داده‌های آموزش تنظیم می‌شود.

این فرآیند از آخرین لایه شبکه شروع می‌شود و مرحله‌به‌مرحله به سمت لایه‌های ابتدایی ادامه می‌یابد — به همین دلیل نام آن Backpropagation است.

اما اجرای این کار برای کل دیتاست بسیار پرهزینه است.

برای کاهش هزینه محاسباتی از روشی به نام Stochastic Gradient Descent) SGD) استفاده می‌شود.

نزول گرادیان تصادفی یا Stochastic Gradient Descent) SGD):

در SGD، ما کل داده‌های آموزشی (مثلاً تصاویر اعداد دست‌نویس) را به هم می‌زنیم -بُر می‌زنیم- و آن‌ها را به مجموعه‌های کوچکتر به نام mini-batch (مثلاً ۱۰۰ تصویر) تقسیم می‌کنیم به ترتیبی که هر min-batch نماینده‌ی خوبی از کل داده‌ها باشد.

سپس Backpropagation را فقط روی یکی از این mini-batch‌ها اجرا می‌کنیم، خطا را محاسبه کرده و وزن‌ها را به‌روزرسانی می‌کنیم. این کار را برای مجموعه بعدی تکرار می‌کنیم و انقدر پیش می‌رویم که با تغییر اعمال شده در وزن‌ها، کاهش محسوسی در هزینه ایجاد نشود.

منابع:

مطلب فوق براساس ‌پلی‌لیست Neural Networks از کانال یوتیوب 3Blue 1Brown تهیه شده است. در این کانال پلی‌لیست‌های مختلفی در حوزه علوم‌کامپیوتر وجود دارد که به شیوه‌ای ساده و قابل فهم، مطالب پیچیده را ارائه می‌کنند.