مطالعه شبکه وابستگی در اقتصاد و چگونگی تاثیر آن بر اقتصاد کلان

چکیده:

اقتصاد پدیده‌ای پویا، چندلایه و غیرخطی است که تبیین دقیق رفتار آن فراتر از متغیرهای کلان سنتی، نیازمند واکاوی ساختار شبکه‌ای  و روابط پیچیده میان صنایع است. این پژوهش با هدف بررسی نقش پیوندهای ورودی–خروجی در انتشار متغیرهای اقتصادی مثل تورم، نشان می‌دهد که شوک‌های اقتصادی بسته به موقعیت توپولوژیک و نوع اتصالات هر بخش در شبکه، به‌صورت ناهمسان، تقویت‌شونده یا با تأخیر زمانی منتقل می‌شوند. اگرچه ریشه‌های این تحلیل در مدل‌های کلاسیک داده–ستانده لئونتیف نهفته است، اما محدودیت‌هایی نظیر فرض خطی‌بودن روابط و نادیده‌گرفتن پویایی رفتاری عوامل اقتصادی، ضرورت گذار به سمت تحلیل‌های پیشرفته شبکه‌ای را آشکار می‌سازد. یافته‌های حاصل از بررسی مدل‌های مدرن تایید می‌کند که شناسایی «صنایع گلوگاهی» و «هاب‌های استراتژیک» از طریق شاخص‌هایی نظیر مرکزیت بوناچیچ و آزمون‌های تنش، ابزاری حیاتی برای پیش‌بینی مسیرهای سرایت بحران و مدیریت تاب‌آوری اقتصادی فراهم می‌آورد. در نهایت، این مطالعه بر اهمیت بومی‌سازی ابزارهای تحلیل شبکه جهت درک عمیق پویایی‌های تورمی در ساختار اقتصادی کشور تأکید می‌کند.

واژگان کلیدی: تورم، تحلیل شبکه‌های پیچیده، مدل داده–ستانده، تاب‌آوری اقتصادی، انتشار شوک

مقدمه

 افزایش قیمت کالاها و خدمات یکی از چالش‌های اساسی اقتصادی در سال‌های اخیر بوده است. وقتی قیمت یک کالا تغییر می‌کند، این تغییر در میان سایر کالاها و بازارها «انتشار» می‌یابد و سرانجام به تورم کلی (شاخص قیمت مصرف‌کننده) یا شاخص قیمت کالاها منجر می‌شود. سوالی که این تحقیق به دنبال آن است که آِیا ارتباطی بین پدیده تورم و  رفتار شبکه‌ای عوامل شکل‌دهنده آن وجود دارد و چگونه از طریق مفاهیم مربوط به شبکه‌های پیچیده می‌توان آن را تحلیل و ارزیابی نمود و در داخل کشور استفاده نمود. در این راستا و به منظور انجام این پژوهش ریزسوالات زیر مطرح گردید:

1.     آیا برای تحلیل تورم نیازمند تحلیل از طریق شبکه‌های پیچیده هستیم؟

2.     تاریخچه استفاده از شبکه‌های پیچیده در اقتصاد  چیست؟

3.     شبکه های استفاده شده برای تحلیل تورم از چه ساختاری برخوردار هستند و چه مواردی را توضیح می‌دهند و چه مواردی را نمی‌توانند هنوز توضیح دهند؟

4.     چه مقالاتی در این زمینه منتشر شده‌اند و چه دستاوردهایی داشته‌اند؟

اهمیت  و ضرورت تحقیق

بسیاری از متغیرهای اقتصادی در قالب فرمولها با متغیرهای ساده قابل تحلیل نیستند. در بسیاری از اقتصادها، «تورم را نمی‌توان صرفاً با چند متغیر کلان ساده مانند نقدینگی، نرخ ارز، کسری بودجه یا انتظارات تورمی توضیح داد»؛ بخش مهمی از رفتار تورم، محصولِ «ساختار شبکه‌ای و پویای اقتصاد» یعنی همان روابط چندلایه، غیرخطی و زمان‌مند بین صنایع، بنگاه‌ها و زنجیره‌های تأمین است. در چنین اقتصادی، تغییر قیمت یک نهاده یا یک شوک عرضه به‌صورت یکنواخت و خطی پخش نمی‌شود؛ بلکه بر اساس مسیرهای خاصی در شبکه تولید حرکت می‌کند و ممکن است در برخی نقاط تقویت، در برخی بخشها تضعیف شود و در برخی جاها با تأخیر زمانی ظاهر گردد. (Leijonhufvud, 1997). برای مثال افزایش قیمت در یک صنعت، به‌ندرت به همان بخش محدود می‌ماند. افزایش هزینه تولید فولاد تنها به صنعت فولاد محدود نمی‌شود؛ بلکه زنجیروار به تولید قطعات خودرو، سپس به قیمت خودرو و در ادامه به هزینه حمل‌ونقل سرایت می‌کند و نهایتاً قیمت کالاهای مصرفی وابسته به حمل‑ونقل نیز افزایش می‌یابد. این الگوی انتشار پیچیده و مسیرمند است و هیچ مدل خطی ساده‌ای قادر به بازنمایی آن نیست.

در بسیاری موارد، شدت واکنش بخش‌ها نسبت به شوک‌ها غیرخطی است. گاهی یک افزایش کوچک در قیمت یک نهاده حیاتی، جهشی بزرگ در هزینه نهایی ایجاد می‌کند که بیش از اثر مستقیم افزایش قیمت آن نهاده است. (Leijonhufvud, 1997) از سوی دیگر اقتصاد واقعی پویاست و بنگاه‌ها رفتار خود را در طول زمان تغییر می‌دهند. Goodwin (1947)  نشان می‌دهد که بنگاه‌ها قادر نیستند ساختار تولید و ترکیب نهاده‌های خود را فوراً تغییر دهند؛ بلکه تعدیل تکنیک‌ها و جایگزینی نهاده‌ها فرآیندی تدریجی و زمان‌بر است. بنابراین فرض «ضرایب فنی ثابت» در تحلیل‌های استاتیک، با واقعیت پویای رفتار تولید سازگار نیست. جایگزینی نهاده‌ها، تغییر در تأمین‌کنندگان، صرفه‌جویی در هزینه یا تغییر فناوری‌ها اموری هستند که به تدریج رخ می‌دهند. برای مثال، در پی افزایش نرخ چرم طبیعی، تولیدکنندگان محصولات چرمی ممکن است به‌تدریج استفاده از چرم طبیعی را کاهش دهند و چرم مصنوعی را جایگزین کنند. این انتقال ممکن است ماه‌ها زمان ببرد و نشان می‌دهد که ضرایب فنی تولید ثابت نیستند. تحلیل تورم بدون در نظر گرفتن این پویایی، تصویر نادرست و ناقصی از فرآیند تورم ارائه می‌دهد. همچنین تورم اغلب به شکل خوشه‌ای ظاهر می‌شود. بخش انرژی، غذا، حمل‌ونقل یا مسکن ممکن است رفتارهای تورمی مشترکی داشته باشند، زیرا در یک خوشه شبکه‌ای قرار دارند. این هم‌حرکتی را نمی‌توان با یک یا دو متغیر کلان توضیح داد، اما از طریق الگوریتم‌های تشخیص خوشه در شبکه‌های ورودی–خروجی می‌توان آن را شناسایی کرد. مثال روشن آن افزایش قیمت گاز طبیعی است که به‌سرعت بر پتروشیمی، پلاستیک، بسته‌بندی و نهایتاً مواد غذایی اثر می‌گذارد؛ اما ممکن است به بخش خدمات مالی تقریباً بی‌اثر باشد و یا افزایش قیمت گوشت قرمز باعث می‌شود فشار تقاضا بر گوشت سفید افزایش یابد و قیمت آن را افزایش دهد حال آنکه بر  سایر محصولات غذایی غیرمرتبط ممکن است تأثیر چندانی نداشته باشد . عامل دیگر رفتار تورم به‌ وسیله حلقه‌های بازخوردی است. مثلاً افزایش قیمت سوخت  باعث افزایش هزینه حمل و نقل می‌گردد که خود یکی از موارد تعیین‌کننده برای قیمت سوخت به جهت حمل از محل تولید تا مصرف است. در چنین چرخه‌هایی، افزایش قیمت در یک بخش می‌تواند چند مرحله بعد دوباره به نقطه شروع بازگردد و تورم را تشدید کند. این الگوهای بازگشتی فقط در مدل‌های شبکه‌ای قابل شناسایی‌اند (Bilgin, 2025). همچنین، شوک‌های قیمتی در بخش‌های مختلف با تأخیر زمانی متفاوت منتقل می‌شوند. افزایش قیمت انرژی ممکن است در همان ماه نخست بر صنایع فولاد و سیمان اثر بگذارد، اما اثر آن بر قیمت خدمات آموزشی یا درمانی ممکن است با فاصله چندین ماه بروز کند. این ناهمگنی زمانی، بخشی بنیادین از پویایی تورم است (Afrouzi & Bhattarai, 2023).

به‌طور خلاصه، تورم پدیده‌ای چندلایه، شبکه‌ای و پویاست و مدل‌های ساده کلان قادر به توضیح کامل آن نیستند. برای فهم دقیق انتقال، شدت، مسیر و زمان‌بندی تورم، ناگزیر باید به تحلیل شبکه‌های پویا در ساختار اقتصادی روی آورد؛ جایی که روابط واقعی اقتصاد نه به‌صورت خطی و ساده، بلکه همچون یک سیستم پیچیده با مسیرهای سرایت، حلقه‌های بازخورد و گلوگاه‌های ساختاری عمل می‌کنند (Afrouzi & Bhattarai, 2023).

نظریات کلاسیک مرتبط با شبکه در علم اقتصاد :

 اقتصاددانان در تبیین بسیاری از پدیده‌ها به آثار شبکه‌ای در علم اقتصاد اشاره می‌کنند. استفاده از شبکه‌های پیچیده پویا از ابزارهای مهم در تحلیل و پیش‌بینی‌های اقتصادی  است. روساریو مانتگنا[1] در سال ۱۹۹۹ اولین مطالعه مهم که در مورد بازارهای سهام بود در مورد استفاده از شبکه‌ها برای تحلیل سیستم‌های اقتصادی پیچیده را انجام داد. از آن زمان تاکنون، تعداد زیادی مطالعه در اقتصاد کلان و اقتصاد مالی از شبکه‌های پیچیده استفاده کرده‌اند. این روش به محققان امکان می‌دهد تا بررسی کنند که شبکه‌ها، چگونه بر نقدینگی بازار و تورم اثر می‌گذارند. برای مثال عجم اوغلو[2] با تحلیل شبکه‌های داده ستانده نشان داد بر خلاف نظرات اقتصاد کلاسیک که معتقد بود طبق قانون اعداد بزرگ شوک‌های بنگاه‌های منفرد اهمیتی برای کل اقتصاد ندارند؛ چون با هم میانگین می‌شوند و اثرشان خنثی می‌شود اگر شبکه ارتباطات بین صنایع نامتوازن باشد، شوک‌های کوچک هم می‌توانند جمع نشوند و حتی تقویت شوند. (2016)

به رغم ماهیت شبکه‌ای اقتصاد، گریز به آن تنها زمانی معمول است که بکارگیری روشهای ساده‌تر جوابگو نباشد. چرا که حمله به سمت آن بسیار دشوار است. لئونتیف[3] می‌نویسد:

 «پژوهشگر از تجربه‌های سخت خواهد آموخت که باید نقطه مقاومتِ سخت را تنها هنگامی مورد حمله قرار داد که تمام قلمروهای همجوارِ آسان‌تر، از پیش به‌طور کامل فتح و بررسی شده باشند.» (1951)

 جدای از پیچیدگیهای مربوط به تحلیل شبکه‌های پویا مشکل مهم دیگری در بررسی متغیرهای اقتصادی از طریق شبکه‌ها وجود دارد و آن ترسیم و یا تعریف خود شبکه است. بر خلاف شبکه‌های پیچیده دیگر نظیر شبکه دنبال‌کنندگان در شبکه‌های اجتماعی و  یا شبکه ارجاعات به مقاله‌ها و ..... که ارتباط بین گره‌ها به وضوح مشخص است و تنها به واسطه گستردگی  و پویایی گره‌ها و نقاط در تحلیل آنها ممکن است دچار مشکل شویم در شبکه‌های مالی و پولی  علاوه بر گستردگی عوامل درهم تنیده، ارتباطات آنها نیز به لحاظ شدت، زمان اثرگذاری و شکل اثرگذاری بسیار پویا، مبهم و غیرشفاف است و ناگزیر از بکار بردن  انتزاع در تعریف شبکه‌ها و فرضیاتی برای ساده‌سازی مساله هستیم.  گودوین در ابتدای مقاله خود که در مورد ارتباطات دینامیک در اقتصاد است می‌نویسد:

«در واقع، پیشرفت در درک هر موضوعی از طریق انتزاع موفق حاصل می‌شود، یعنی تشخیص اینکه چه چیزهایی را می‌توان نادیده گرفت و چه چیزهایی را نمی‌توان نادیده گرفت.» (Goodwin, 1947)

 اولین تلاش در زمینه ایجاد یک شبکه تحلیلی در علم اقتصاد را باید احتمالا به  لئونتیف نسبت داد. هرچند در زمان وی نظریه شبکه‌های پیچیده وجود نداشت و گراف‌ها فقط در ریاضیات نظری استفاده می‌شدند. اما کاری که لئونتیف کرد این بود که ساختار اقتصاد را در قالب یک ماتریس وابستگی متقابل نشان داد. وی در دهه 1930 برای تحلیل اقتصاد آمریکا جدولی ابداع نمود که آن را جدول  روابط داده ستانده[4] نامگذاری نموده بود و در کتاب خود  که بعدها نوشت آن را چنین توضیح می‌دهد:

 «از دیدگاه طرح داده- ستانده، هر اقتصاد ملی را می‌توان به‌عنوان یک سیستم صنایع مرتبط متقابل یا فعالیت‌های اقتصادی وابسته به یکدیگر توصیف کرد. این روابط در واقع به شکل جریان‌های نسبتاً پایدار کالا و خدمات است که به‌صورت مستقیم یا غیرمستقیم، تمام بخش‌های اقتصاد را به یکدیگر پیوند می‌دهد. این جریان‌ها را می‌توان به‌صورت کمی مشاهده و توصیف کرد.» (Leontief,1951)

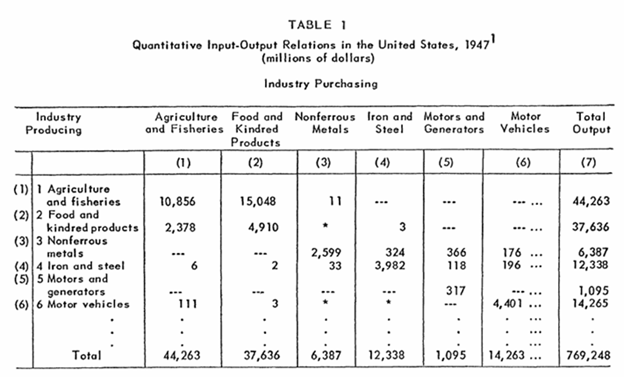
در جدولی که وی ابداع نمود اقتصاد کشور به 50 بخش مثل بخش کشاورزی، فولاد، صنایع غذایی و .. بخش‌بندی شده بود. صنایع خارجی نیز  به صورت یک بخش مجزا درنظر گرفته شده بود. همچنین دو بخش خانوار و دولت نیز به عنوان مصرف‌کننده نهایی در جدول لحاظ شده بود که البته هیچ محصولی تولید نمی‌نمودند.  ابن بخش‌ها به صورت متقارن در داخل 50 ردیف و 50 ستون قرار می‌گرفتند . هر سطر نشان‌دهنده تولید یک صنعت و  هر ستون نشان‌دهنده مصرف یک صنعت از تولید سایر صنایع بود.   مقدار در خانه i,j  نشان می‌داد که صنعت i  چقدر از تولید صنعت j  بر حسب ارزش پولی استفاده کرده است.

البته زمان لئونتیف روش استانداردی برای درج اعداد در این جدول وجود نداشت و او با استفاده از گزارشهای پراکنده و سرشماریهای آماری خانه‌های این جدول را تکمیل نمود.  اما امروز صنایع بسیار پیچیده‌تر شده‌اند. یک صنعت چند محصول تولید می‌کند و یک محصول توسط چند صنعت تولید می‌شود و خدمات واسطه رشد کرده است. مالیات‌ها، یارانه‌ها، حمل‌ونقل و تجارت خارجی نیز جداگانه تعریف می‌شوند. بنابراین دیگر نمی‌توان مثل زمان لئونتیف از «داده‌های هزینه» مستقیماً جدول متقارن ساخت. هم‌اکنون این جدول در قالب استاندارد بین‌المللی SNA که توسط پنج سازمان شامل سازمان ملل، صندوق بین‎المللی پول، بانک جهانی، OECD و ٍٍEurostat تدوین می‌شود تهیه و به‌روزرسانی می‌گردد.

در ایران جدول داده ستانده برای اولین بار توسط وزارت اقتصاد در سال 1344 تهیه گشت. جدیدترین آن نیز در سال 1395 توسط مرکز آمار برای 82 رشته فعالیت با 155 محصول منتشر گردیده است. (مرکز آمار ایران، 1395)

جداول متقارنی که مرکز آمار تهیه نموده است هرچند صریحا در گزارش قید نگردیده است ولی باید آن را تقریباً منطبق بر استاندارد تدوین شده توسط SNA دانست که بر اساس عرضه و تقاضا[5] محاسبه شده است. در این جدول ابتدا هزینه مصرفی هر بخش از خریداری هر محصول در دو جدول  که یکی بر حسب قیمت تولیدکننده و دیگری قیمت مصرف‌کننده است محاسبه می‌گردد. سپس میزان عرضه هر یک از آن 155محصول توسط 82 شرکت بر حسب قیمت تولیدکننده در جدول دیگر تهیه گردیده است. این سه جدول اطلاعات پایه را برای محاسبه ورودی و خروجیهای هر بخش محاسبه می‌نمایند و جداول متقارن که نشان‌دهنده ارزش ریالی مورد استفاده هر بخش از بخش دیگر است از آن مستقیما به واسطه فرمولهای محاسبه که از ضرب ماتریسها و ماتریس وارون بهره می‌برند محاسبه می‌گردد.

اما جدول داده ستانده به رغم کاربردهای فراوانی که دارد در مدلهای پایه آن هنوز برای تحلیل بسیاری از پدیده‌های اقتصادی کافی نیست. برای مثال دو محدودیتی که خود لئونتیف نیز از ابتدا اشاره کرده بود آن بود که این جدول اثرات روانی و رفتار مصرف‌کنندگان را لحاظ نمی‌کند و تنها روابط مالی و مادی صنایع را دنبال می‌کند. همچنین دینامیک اقتصادی یا تغیرات تکنولوژیک و تفاوتهای زمانی را نیز در اثرگذاری لحاظ نمی‌کند و فرض می‌کند همه روابط در یک زمان واحد رخ می‌دهد.

گودوین تلاش نمود روابط دینامیک را در اقتصاد  چندبخشی به مدل لئونتیف اضافه نماید. اما برای این کار راه‌حل او خلاص شدن از آثار شبکه‌ای اقتصاد بود. او بیان نمود شرط بررسی روابط دینامیک خارج از شبکه و به صورت ساده غیر متقارن بودن آن است. برای مثال صنعت خودرو و فولاد ارتباط دینامیک غیرمتقارن با یکدیگر دارند. چون در زمانی که عرضه فولاد با یک شوک مواجه می‌گردد صنعت خودرو چون با آلترناتیو دیگری مواجه نیست با مشکل مواجه می‌گردد و آن هم دچار شوک می‌گردد. ولی اگر در تقاضای مصرفی از سوی بخش خودرو مشکلی پیش‌بیاید اگر بخش فولاد با صنایع متعدد دیگری درگیر باشد این وابستکی نمی‌تواند تاثیر زیادی بر روی بخش فولاد بگذارد.  لذا در این حالت می‌توان سمت ضعیف‌تر ارتباط را حذف نمود تا مسائل را بتوان ساده‌تر حل نمود.(Goodwin, 1947) هرچند این ساده‌سازی همانطور که خود او می‌گوید همیشه جواب نمی‌دهد و ما را نمی‌تواند از رویکرد شبکه‌ای فارغ نماید‌.

 نقد وارد دیگر بر مدل لئونتیف فرض او بر خطی بودن روابط بین بخشی است. در مدل‌های ساده، ممکن است اثرات مستقیم یک نهاده یا محصول دیده شود، اما اثر تجمعی و تقویت‌شده از مسیرهای چندمرحله‌ای و هم‌افزایی‌های داخل شبکه دیده نمی‌شود. وقتی یک محصول چندین صنعت را تحت تأثیر قرار می‌دهد و صنایع دیگر هم با هم مکمل هستند، شوک چند برابر و غیرخطی روی کل اقتصاد ظاهر می‌شود این همان چیزی است که مدل‌های سنتی لئونتیف و تحلیل‌های خطی ساده نمی‌توانند کاملاً نشان دهند.

مدلهای مدرن تحلیل شبکه در علم اقتصاد

یکی از عواملی که شروع تحلیل‌های شبکه‌ای مدرن را در اقتصاد به تاخیر انداخت نظریه لوکاس بود.. لوکاس بیان داشت اثرات خرد درون شبکه طبق قانون اعداد بزرگ همدیگر را خنثی می‌نمایند و شوکهای خرد نمی‌توانند اثرات بزرگی ایجاد نمایند. لذا مطالعه آنها بی‌ثمر است. پذیرش نظریه لوکاس بدین معنا بود که مطالعه ساختارهای شبکه‌ای مثل لئونتیف امر بیهوده‌ای است و متغیرهای اقتصادی فارع از ساختار شبکه به صورت خطی بر روی اقتصاد کلان اثر می‌کنند.

اما مشاهده بسیاری از تجارب اقتصادی و تحلیل آن که از طریق روشهای معمول امکان‌پذیر نبود بالاخره اقتصاددانها را وادار به تحلیل شبکه و شناخت ساختارهای شبکه‌ای نمود. امری که با یک تاخیر از ابتدای قرن جاری شروع شد و هنوز به نظر می‌رسد با پختگی کامل فاصله زیادی دارد و در اینجا به برخی از نمونه‌های شاخص آن اشاره می‌کنیم.

پژوهش اول: تحلیل ساختاری شبکه‌های صنعتی و ارتباط آن با تاب‌آوری اقتصادی منطقه‌ای (Qiao & Ji, 2021)

پژوهش حاضر با عنوان  تمرکز بر نابرابری‌های منطقه‌ای در چین، به واکاوی علل تفاوت در سطح تاب‌آوری استان‌ها در مواجهه با شوک‌های اقتصادی، به‌ویژه بحران مالی ۲۰۰۸، می‌پردازد. مسئله بنیادین در این راستا، تمرکز نامتقارن منابع و صنایع پیشرفته در قطب‌های خاص است که منجر به شکل‌گیری ساختارهای توسعه‌ای نامتوازن گشته است؛ پدیده‌ای که علاوه بر چین، در بسیاری از کشورهای عضو OECD نیز مشهود است. اگرچه افزایش پیوندهای اقتصادی میان مناطق می‌تواند کارایی سیستم را ارتقا بخشد، اما هم‌زمان پتانسیل آسیب‌پذیری در برابر شوک‌های بیرونی را نیز تشدید می‌کند. بر این اساس، مفهوم «تاب‌آوری اقتصادی منطقه‌ای» به معنای توانمندی یک سیستم برای مقاومت، بازیابی، بازآرایی و تجدید مسیر رشد، چارچوب اصلی این تحلیل را تشکیل می‌دهد (Qiao & Ji, 2021).

نوآوری محوری این مطالعه، به‌کارگیری نقشه‌نگاری ساختارهای شبکه‌ای در حوزه اقتصاد منطقه‌ای است. در این مدل‌سازی، اقتصاد هر استان به مثابه یک شبکه پیچیده صنعتی در نظر گرفته می‌شود که در آن صنایع در نقش گره‌ها و روابط داده-ستانده، وابستگی‌های تولیدی-مصرفی و همبستگی‌های صنعتی در نقش پیوندها عمل می‌کنند. وزن این پیوندها که نشان‌دهنده شدت وابستگی متقابل است، از طریق ترکیب ضرایب عرضه و تقاضا و بر اساس جداول داده-ستانده استانی استخراج شده است. این رویکرد اجازه می‌دهد تا «معماری درونی اقتصاد منطقه» با دقت بالایی ترسیم شود (Qiao & Ji, 2021).

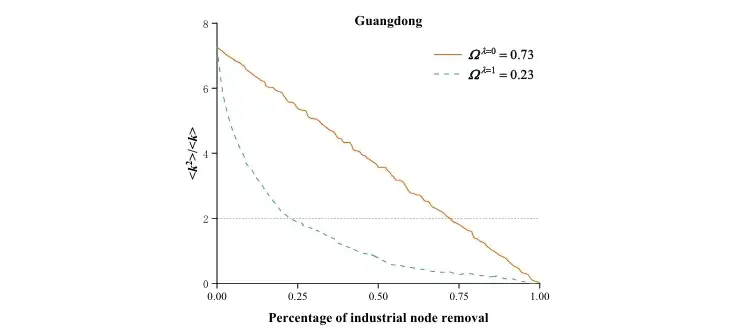
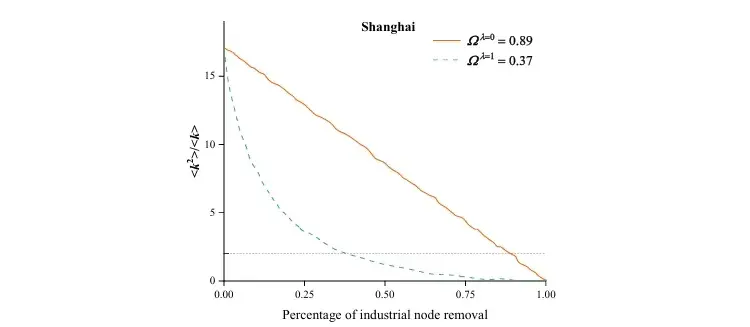
از منظر نظریه شبکه‌ها، اقتصاد منطقه‌ای یک سیستم پیچیده با آستانه‌های بحرانی مشخص تلقی می‌شود. یافته‌های حاصل از اجرای آزمون تنش نشان می‌دهد که حذف صنایع به صورت تصادفی یا هدفمند (حذف هاب‌های با درجه اتصال بالا) می‌تواند به فروپاشی ساختاری منجر شود. در شبکه‌هایی که حول چند هاب مرکزی سازمان‌یافته‌اند، نوعی پارادوکس مشاهده می‌شود: این سیستم‌ها در برابر شوک‌های تصادفی مقاوم، اما در برابر حذف هدفمند گره‌های کلیدی به‌شدت آسیب‌پذیرند. بنابراین، ویژگی‌های توپولوژیک شبکه و نحوه توزیع پیوندها، تعیین‌کننده نهایی سطح تاب‌آوری منطقه‌ای است (Qiao & Ji, 2021).

نتایج تجربی این پژوهش تایید می‌کند که استان‌های دارای شبکه‌های صنعتی منسجم‌تر و مستحکم‌تر، در طول بحران ۲۰۰۸ افت کمتری را در نرخ اشتغال تجربه کرده‌اند. نکته حائز اهمیت این است که صرفِ «تنوع صنعتی» برای تضمین ثبات کافی نیست، بلکه نحوه اتصال و معماری پیوندها اهمیت بیشتری دارد. در این میان، مفهوم «تنوع مرتبط[6] به عنوان یک تیغ دو لبه عمل می‌کند؛ چرا که پیوند میان صنایع هم‌خانواده می‌تواند از سویی نوآوری را تقویت کرده و از سوی دیگر به کانالی برای انتشار سریع زنجیره‌ای بحران تبدیل شود (Qiao & Ji, 2021).

در نهایت، این مطالعه پیشنهاد می‌دهد که برای درک عمیق تاب‌آوری باید از الگوهای تعادلی سنتی عبور کرد و به سمت تحلیل نقشه‌ای وابستگی‌های صنعتی حرکت نمود. ویژگی‌هایی نظیر درجه اتصال گره‌ها، وجود هاب‌های استراتژیک و آستانه فروپاشی شبکه، شاخص‌های کلیدی برای ارزیابی ثبات اقتصادی هستند. از منظر سیاست‌گذاری، این رویکرد که تلفیقی از جغرافیای اقتصادی تکاملی و علم شبکه است، ایجاب می‌کند که برنامه‌های توسعه منطقه‌ای نه تنها بر تنوع‌بخشی، بلکه بر تقویت و بهینه‌سازی ساختار شبکه‌ای برای جلوگیری از سرایت شوک‌ها متمرکز شوند.

پژوهش دوم: تحلیل ساختاری شبکه تأمین و عملکرد مالی بنگاه‌ها در شرایط بحران (Orenstein & Zhang, 2023)

این پژوهش با اتخاذ رویکردی نوآورانه در تلاقی «علم شبکه‌ها» و «اقتصاد مالی»، به بررسی چگونگی تأثیر هندسه و ساختار روابط یک شرکت با تأمین‌کنندگان بر ارزش بازار آن در دوران بحران (مانند پاندمی کووید-۱۹) می‌پردازد. محققان با تمرکز بر داده‌های بازه زمانی ۲۰۱۸ تا ۲۰۲۲ دو شرکت پیشرو در صنعت خودرو، فورد و جنرال موتورز، و با بهره‌گیری از تکنیک‌های داده‌کاوی، شبکه‌های تأمین این شرکت‌ها را به گونه‌ای پالایش کردند که تنها گره‌های حیاتی در جریان واقعی ارزش محصول باقی بمانند. دستاورد محوری این مطالعه اثبات آماری این نکته است که شاخص‌های ساختاری شبکه، از جمله «متوسط درجه» و «ضریب خوشه‌بندی» ، تأثیر مستقیم و معناداری بر شاخص Tobin’s Q  به عنوان نماد ارزش بازار شرکت دارند.

یکی از یافته‌های کلیدی و چالش‌برانگیز این مطالعه، شناسایی رابطه معکوس میان «متوسط درجه» (تعداد اتصالات) و عملکرد مالی است. برخلاف دیدگاه‌های سنتی که کثرت تأمین‌کنندگان را نشانه قدرت و توزیع ریسک می‌دانستند، این پژوهش نشان می‌دهد که افزایش بی‌رویه لبه‌ها و اتصالات در شبکه، به دلیل ایجاد پیچیدگی‌های مدیریتی و تحمیل هزینه‌های نظارتی سنگین، در نهایت منجر به کاهش ارزش بازار شرکت می‌شود. در مقابل، پژوهش بر اهمیت «کیفیت و فشردگی روابط» تأکید می‌ورزد؛ به طوری که بالا بودن ضریب خوشه‌بندی و تراکم شبکه به عنوان سیگنالی مثبت برای بازار عمل می‌کند. این ویژگی‌ها نشان‌دهنده توانمندی شرکت در انتقال سریع اطلاعات و منابع در زمان بحران است، چرا که در شبکه‌هایی با خوشه‌بندی بالا، تأمین‌کنندگان خود نیز با یکدیگر در ارتباط بوده و تاب‌آوری سیستماتیک بیشتری ایجاد می‌کنند.

در نهایت، تحلیل تطبیقی میان فورد و جنرال موتورز نشان می‌دهد که پویایی ساختار شبکه چگونه به یک مزیت رقابتی تبدیل می‌شود. یافته‌ها حاکی از آن است که شبکه جنرال موتورز به دلیل اتکای مفرط به گره‌های مرکزی و بزرگ، در برابر شوک کووید-۱۹ آسیب‌پذیری بیشتری نشان داد؛ در حالی که شرکت فورد با بهره‌گیری از شبکه‌ای منعطف‌تر و ساختاری که وابستگی کمتری به گره‌های خاص داشت، توانست ارزش بازار خود را به شکل بهتری حفظ نماید. دستاورد بزرگ این تحقیق، تبدیل مفهوم انتزاعی «تاب‌آوری» به معیارهای ریاضی دقیق است که امکان ارزیابی پایداری مالی بنگاه‌ها را بر اساس توپولوژی شبکه فراهم می‌سازد. بر این اساس، ثابت می‌شود که در اقتصاد مدرن، «تناسب ساختاری» شبکه تأمین، از «وسعت» آن حیاتی‌تر است.

پژوهش سوم: شبکه‌ها، شوک‌ها و ریسک سیستمیک (Acemoglu et al., 2015)

عجم‌اوغلو و همکاران در این پژوهش بنیادین، به تحلیل توپولوژی شبکه‌های اقتصادی و سازوکارهای انتشار نوسانات در بستر این شبکه‌ها می‌پردازند. هدف اصلی این مطالعه، تبیین این مسئله است که چگونه ساختار اتصالات میان گره‌ها می‌تواند شوک‌های خردِ محلی را میرا کرده و یا برعکس، آن‌ها را به بحران‌های سیستمیک در کل گراف شبکه تبدیل کند. این پژوهش چون همراستایی بیشتری با اهداف این پژوهش دارد با جزییات بیشتری توضیح داده می‌شود.

آنها بدین منظور از مدل‌های  شکل-کاهش یافته در شبکه استفاده می‌کنند. مدل شکل-کاهش‌یافته بدین معنا است که فقط به روابط نهایی پس از متعادل شدن سیستم پس از یک شوک نگاه می‌شود. برای مثال ما کاری نداریم در ذهن مدیر کارخانه چه می‌گذرد؛ فقط رصد می‌کنیم که وقتی قیمت برق بالا رفت، او قیمت محصولش را چقدر بالا می‌برد. بدین ترتیب تمام جزئیاتِ روان‌شناختی و انگیزشی که مدل را پیچیده می‌نماید حذف می‌گردد.

 این مدل از اجزای زیر تشکیل شده است:

۱. تابع تعامل نسبتاً عمومی که وابستگی وضعیت هر عامل را به عوامل دیگر نشان می‌دهد.

۲. شبکه تعاملات که مشخص می‌کند این معیارهای خلاصه، چگونه به‌عنوان تابعی از وضعیت سایر عامل‌ها تعیین می‌شوند.

۳. تابع تجمیع که توصیف می‌کند چگونه وضعیت‌های سطحِ عامل، در کنار هم متغیرِ کلانِ مورد نظر را شکل می‌دهند.

در مدل داده ستانده، مصرف‌کننده نهایی «ایستگاه آخر» است و منطقاً همه‌چیز باید همان‌جا تمام شود. اما در مدل شبکه‌ای عجم‌اوغلو، ماجرا متفاوت است. مصرف‌کننده نهایی خودش یک گره در شبکه است، نه یک نقطه خارج از آن.

عجم اوغلو و همکاران برای مدل‌سازی انتشار شوک در یال‌ها، از یک تابع انتقال به نام f  استفاده می‌کنند که طبق رابطه زیر تعریف می‌شود:

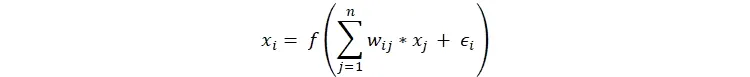
در اینجا wij وزن یال بین عامل i و j در ماتریس مجاورت شبکه W است. ϵi  شوک مستقل و ناشی از خودِ عامل i است.

آنچه در اینجا از اهمیت کلیدی برخوردار است، وضعیت هر عامل i  است که با xi نشان داده می‌شود؛ این متغیر، انتخابِ عملِ آن عامل مانند میزان تولید یا سرمایه‌گذاری یا هر متغیر اقتصادی مورد نظر دیگر (مانند توانایی پرداخت بدهی یک نهاد مالی) را نشان می‌دهد. وی در توضیح این مطلب می‌نویسد:

«فرقی نمی‌کند مدل درباره تولید باشد یا بازارهای مالی؛ اصل ماجرا این است که گره‌ها بر هم اثر می‌گذارند و این یعنی راه برای «سرایتِ» شوکِ یک گره به کل اقتصاد باز است.»

مقدار ثابت wij  در رابطه فوق، میزان تعامل بین عامل‌های i و j  را نشان می‌دهد. به طور مشخص، wij  بزرگتر به این معناست که وضعیت عامل i  نسبت به وضعیت عامل j  حساس‌تر است؛ در حالی که wij=0  به این معنی است که عامل j  تأثیر مستقیمی بر وضعیت عامل i  ندارد. بدون آنکه از کلیت موضوع کاسته شود، فرض می‌کنیم مجموع وزن‌ها برای هر عامل برابر با یک است. این امر تضمین می‌کند که میزان وابستگی هر عامل به مجموع سایر عامل‌ها، مقداری ثابت است.

با شناخت تابع f، تعاملات بین عامل‌ها را می‌توان به‌وسیله یک گراف وزن‌دار و جهت‌دار با n  رأس نیز به دست آورد که آن را  می‌توان شبکه تعاملات اقتصاد نامید. هر رأس در این شبکه متناظر با یک عامل است و یک یال جهت‌دار از رأسj  به رأس i  وجود دارد. اگر wij > 0  باشد؛ به این معنا است که وضعیتِ عامل i  مستقیماً تحت تأثیر وضعیتِ عامل j  قرار دارد.

در نهایت وضعیتِ کلانِ اقتصاد به صورت زیر تعریف می‌گردد.

y = g(h(x1) +h(x2)+…. + h(xn))

که در آن g  و h  توابعی از مجموعه اعداد حقیقی به اعداد حقیقی و y  نشان‌دهنده یک خروجی اقتصاد کلانِ مورد نظر است که از تجمیع وضعیت‌های فردیِ تمامی عامل‌ها به دست می‌آید. g نیز تابع تجمیعِ اقتصاد است که وضعیت کلان را نشان می‌دهد. این فرمول مثل یک ماشین عمل می‌کند. ابتدا اقدامات تک‌تک افراد xi  را می‌گیرد، آن‌ها را از فیلتر تابع h  رد می‌کند، با هم جمع می‌زند و در نهایت کلِ حاصل را از فیلتر تابع g  عبور می‌دهد.

 با در نظر گرفتن وقوع شوک‌های

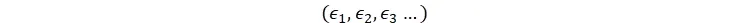
، تعادلِ اقتصاد مجموعه‌ای از وضعیت‌های

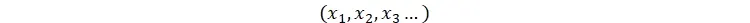
 است به‌طوری که معادله اول آنهابرای تمامی عامل‌های i به طور هم‌زمان برقرار باشد. بدین معنا که اول  شوک‌هااتفاق می‌افتند (مثلاً قیمت دلار ناگهان جهش می‌کند یا جنگی رخ می‌دهد.)  سپس، گره‌ها با هم تعامل می‌کنندتا به یک وضعیت پایدار  برسند، به گونه‌ای که تابع f برای همه وضعیت‌ها در شرایط بعد از شوک دوباره صدق نماید.

از نظر آنها خروجی نهایی سیستم نه تنها به وزن یال‌ها، بلکه به ویژگی‌های مشتق‌پذیری این تابع بستگی دارد که تعیین‌کننده رفتار سیستم در گذر از حالت عادی به بحران است. برای شناخت مرز دو حالت عادی و بحران دو سناریوی زیر با توجه به تابع تعامل تعریف می‌گردد.

آنها در مفروضات مساله می‌نویسند ما بر اقتصادی تمرکز می‌کنیم که در آن شوک‌های سطحِ عامل کوچک هستند. این فرض آنها را قادر ‌ساخت تا وضعیت تعادلیِ هر عامل و وضعیت اقتصاد کلان را که از اثرات چرخش چندباره یک شوک در داخل شبکه حاصل می‌گردد به‌ وسیله چند جمله اولِ بسط تیلورِ آن‌ها تقریب بزنند. حال آنکه در تورم‌های بالا، رفتارهای دفاعیِ عامل‌ها (مثل احتکار، انتظارات تورمی و پیش‌خور کردن گرانی) فعال می‌شود. این رفتارها عواملی هستند که در اعداد کوچک (۲ و ۳ درصد) خواب بوده‌اند، اما در اعداد بزرگ بیدار می‌شوند و رفتار تابع را پیش‌بینی ناپذیر می‌نمایند.

آنها اولین نتیجه این مدلسازی را چنین بیان می‌نمایند:

«در یک دنیای خطی، عملکرد کلان اقتصاد در حالت میانگین، به جزئیات پیچیده شبکه تعاملات زیربنایی آن بستگی ندارد.»

در اقتصاد خطی اگر قیمت بنزین ده درصد گران شود و اثرش بر حمل‌ونقل پنج درصد باشد، وقتی بنزین بیست درصد گران شود، اثرش بر حمل‌ونقل حتماً باید ده درصد باشد. در این حالت اقتصاد خطی و کاملاً پیش‌بینی پذیر می‌گردد. امری که آن را معادل اطمینان[7] می‌نامند.  اگر فرض کنیم همه چیز خطی است، شبکه بی‌اهمیت می‌شود. هرچند به تجربه چنین رفتار منظمی را معمولاً مشاهده نمی‌کنیم و می‌توان نتیجه گرفت که اقتصاد امری غیرخطی است. یعنی اگر مجموعه‌ای از شوک‌های کوچک مثبت و منفی به اقتصاد وارد شود، این‌ها دیگر همدیگر را خنثی نمی‌کنند. به دلیل غیرخطی بودن، ممکن است برآیندِ چند شوک کوچک که قاعدتاً باید صفر می‌شد، ناگهان به یک تورم بزرگ تبدیل شود.

توصیف نظریه بازی ها طبق مدل شبکه پیشنهادی  عجم اوغلو:

یک بازی با n  بازیکن و با اطلاعات کامل را در نظر بگیرید[8] که در آن تابع مطلوبیت (سود) عامل i  به صورت زیر داده شده است:

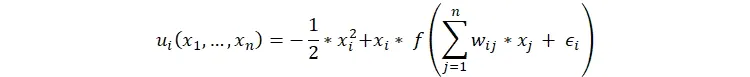
در اینجا xi  اقدامی است که بازیکنi  انجام می‌دهد (مثلاً میزان تلاش یا سرمایه‌گذاری). wij  وزن شبکه است که نشان‌دهنده قدرت و نوع اثرگذاری بازیکن j  روی بازیکن i  است. F  تابع تعامل است که قبلا توضیح داده شد و نشان می‌دهد که اقدامات دیگران چگونه بر مطلوبیت فرد اثر می‌گذارد و ϵi اثر مستقل از عوامل همسایه است که بر پاداش فرد اثر می‌گذارد.

این تابع حاصل‌جمع دو عبارت است که بخش اول  که منفی است هزینه‌ایست که بابت بیشینه‌سازی سود پرداخته می‌شود و بخش دوم نتایج حاصل از تلاش مذکور است و به صورت فرمول فوق فرض شده است. در شبکه‌ای که الگوی فوق برقرار باشد چون مشتق دوم منفی است، بیشترین سود برای هر بازیکن زمانی به دست می‌آید که مشتق اول تابع فوق صفر گردد و این همان معادله اول است که در ان تعادل نش برقرار می‌شود؛ یعنی وضعیتی که در آن، هیچ بازیکنی نمی‌تواند با تغییرِ «تنهاییِ» استراتژی خود، وضعیتش را بهتر کند؛ به شرطی که بقیه بازیکنان استراتژی‌شان را تغییر ندهند. اگر تابع f صعودی باشد معنای آن این است که هرچه اطرافیان ما بیشتر تلاش کنند، سود ما از تلاش بیشتر، افزایش می‌یابد (مثل یادگیری یک زبان جدید یا استفاده از یک پیام‌رسان) که این حالت مکمل استراتژیک نامیده می‌شود و وقتی تابع f نزولی است معنای آن این است که با افزایش تلاش دیگران، نیاز به تلاش کمتری برای ما هست و یا xi بهینه کمتری نسبت به زمان قبلی که همسایه ما تلاش ننموده بود داریم. این حالت را جایگزین استراتژیک می‌نامند.

یک زیرگروه ساده شده از تابع  f آن است که نتیجه آن برابر ضریب ثابت α که یک مقدار مابین صفر و یک است ضربدر ورودی تابع باشد. در این حالت رابطه قبلی به شکل زیر درخواهد آمد.

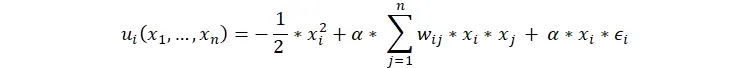
اگر مثل قابل حالت بهینه را حساب نماییم خواهیم داشت:

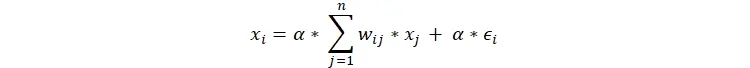
حال اگر معادله اول را برای هر n گره بنویسیم، n معادله خطی با n مجهول خواهیم داشت که به طریق جبر ساده خطی حل خواهد شد. برای تعیین سطح کلان جامعه نیز دو راه داریم. یکی آنکه مجموع تلاش جامعه را حساب کنیم. در این حالت فعالیت مجموع جمع کل اقدامات همه بازیکنان خواهد شد. یعنی برای متغیر کلان g(z) = h(z) = z و دیگر آنکه رفاه کل جامعه را حساب کنیم.

همچنین اگر معادله بالا را در تابع سود جایگزاری نماییم خواهیم داشت

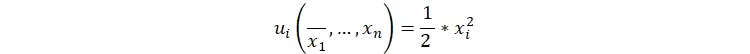
و این یعنی رفاه کل جامعه برابر است با

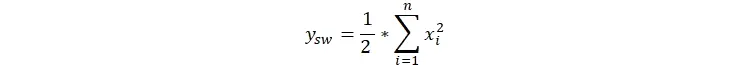
در این متغیر کلان توابع g و h  به صورت  g(z) = z و h(z) = z2/2 هستند.

حال اقتصادی شامل n بنگاه (یا بخش) رقابتی را در نظر بگیرید که با {1, 2,……, n}  نشان داده می‌شوند و هر یک کالای متمایزی تولید می‌کنند. هر محصول می‌تواند یا توسط توده‌ی مصرف‌کنندگان مصرف شود و یا به عنوان نهاده (کالای واسطه‌ای) برای تولید کالاهای دیگر به کار رود. تمام بنگاه‌ها از فناوری تولید کاب-داگلاس[9] با بازدهی ثابت نسبت به مقیاس[10] استفاده می‌کنند که نیروی کار و کالاهای واسطه‌ای را به محصول نهایی تبدیل می‌کند  و  تولید در معرض نوعی شوک فناوری خاص (ایدیوسینکراتیک) قرار دارد. به طور مشخص‌تر، خروجی بنگاه i که آن را با Xi  نشان می‌دهیم، برابر است با:

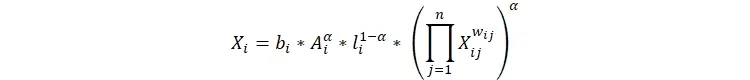
که در آن Ai  شوک بهره‌وری مربوطه؛ li  مقدار نیروی کار استخدام شده توسط بنگاه i ؛ xij  مقدار کالای j  که برای تولید کالای i  استفاده شده است؛ bi  یک مقدار ثابت و α که عددی بین صفر و یک است؛ بیانگر  سهم کالاهای واسطه‌ای در تولید است. توان wij   در معادله بالا، سهم کالای j در فناوری تولید کالای i را نشان می‌دهد. wij بالاتر به معنای آن است که کالای j در تولید i اهمیت بیشتری دارد، در حالی که wij = 0  به این معنی است که کالای j  نهاده‌ی مورد نیاز برای فناوری تولید i نیست. فرض بازدهی ثابت نسبت به مقیاس نیز ایجاب می‌کند که برای تمام بنگاه‌ها، مجموع سهم‌ها (مقدار w) برابر با یک باشد.

اقتصاد همچنین شامل توده‌ی واحدی از مصرف‌کنندگان یکسان (همسان) است. هر مصرف‌کننده صاحب یک واحد نیروی کار است که می‌تواند توسط بنگاه‌ها برای اهداف تولیدی استخدام شود. ما فرض می‌کنیم که مصرف‌کننده‌ی نماینده، دارای ترجیحات متقارن کاب-داگلاس نسبت به n  کالای تولید شده در اقتصاد است. یعنی همیشه درصد ثابتی از درآمدش را به صورت مساوی (برای ساده‌سازی مساله)  خرج هر نوع کالا می‌کند، فارغ از اینکه آن کالا چقدر گران یا ارزان شود. برای مثال اگر قیمت کالایی دو برابر شود، او دقیقاً مصرفش را نصف می‌کند تا همان  هزینه سابق را حفظ کند. در این حالت مطلوبیت کلان به صورت زیر حساب می‌گردد.

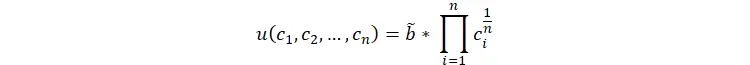
که در آنci   مقدار مصرف کالای i  و b  یک ثابت مثبت است.

با توجه به این مساله هر بنگاه برای اینکه سودش را بهینه کند از قاعده زیر تبعیت می‌کند.

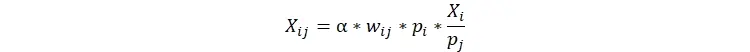
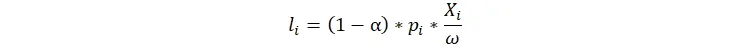
که ω دستمزد نیروی کار و pi قیمت کالای i است. بدین ترتیب مدیر به اندازه

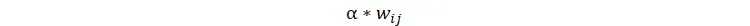
 از درامدش را صرف خرید کالای j می‌کند و به اندازه

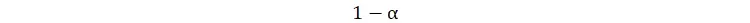
 از درامدش را صرف نیروی کار و پرداخت حقوق می‌کند. توضیح شهودی این مطلب بدین صورت است که که در تابع کاب-داگلاس، توانِ هر بخش نشان‌دهنده میزانِ اهمیت و بهره‌وریِ حاشیه‌ایِآن ماده است و بهینه‌ترین حالت آن است که هر چیز  دقیقاً به اندازه اهمیتِ آن هزینه شود و یا به عبارت دیگر هزینه اضافه بابت بک نهاده تا زمانی مطلوب است که به درآمد بیشتری از هزینه‌ای که بابت آن داده‌ایم منتهی شود.

بدین ترتیب درآمد هر شرکت از دو بخش مصرف‌کننده نهایی که برابر سهم خرید آن بخش از دستمزد نیروی کار است[11]  و سایر بخش‌ها که به صورت زیر نشان می‌دهیم.

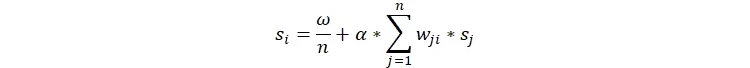
که si برابر درآمد شرکت و برابر قیمت کالا ضربدر مقدار فروش آن است.[12] انها حالا یک متغیر جدید به نام ضریب نفوذ و با علامت  ζ تعریف می‌کنند که برابر است با سهمی که هر بخش از جریان پولی در جامعه صرف خرید آن می‌شود به طوری که si = piXi = ζiω . پس Xij = α*wij*ζi*Xj/ζj  و li = (1 − α)ζi با جایگذاری این دو فرمول در معادله‌ای که میزان خروجی هر بنگاه را مشخص می‌کرد داریم:

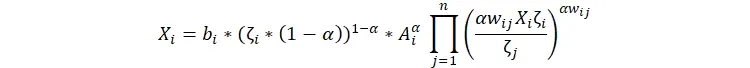
بدین طریق ما متغیر قیمت را حذف می‌کنیم. چرا که معمولا قیمت‌ها متغیر هستند ولی تناسب مصرف آنها برای هر بخش ثابت است.حال اگر از طرفین معادله لگاریتم بگیریم و xi  برابر log(Xi) باشد به معادله زیر می‌رسیم.

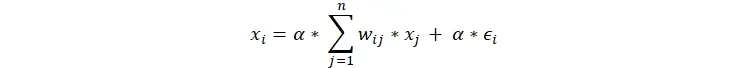
البته در فرمول فوق با توجه به اینکه bi  یک ضریب ثابت و تنها  برای همتراز کردن دو طرف معادله است آن را به گونه‌ای فرض می‌کنیم که مجموعش با مقادیر ثابت خنثی گردد و آنها را حذف نماید. راز این ساده‌سازی در این است که در اقتصاد کلان و تحلیل شبکه، ما به دنبال این هستیم که اگر متغیر A  یک درصد تغییر کرد، متغیر B  چند درصد تغییر می‌کند. این «درصد تغییرات» تحت تأثیر ضرایب ثابت (مثل bi)  قرار نمی‌گیرد. بنابراین حذف آن‌ها با استفاده از انتخاب مقدار مناسب برای bi، پاسخ‌های نهایی مدل درباره اثرات شبکه را تغییر نمی‌دهد. بدین ترتیب می‌توان دریافت مدل داب-داگلاس حالت دیگری نیز از همان شبکه ماتریسی است که در قبل بیان شد.

عجم‌اوغلو و همکاران در سومین گام، چارچوب خود را بر مدل‌های سرایت مالی  تطبیق می‌دهند. در این مدل، گره‌ها «بانک‌ها» هستند و یال‌ها نشان‌دهنده «بدهی‌های بین‌بانکی» می‌باشند.

در این اقتصاد، n  مؤسسه مالی داریم که از طریق قراردادهای بدهی به هم متصل‌اند. هر بانک i  مطالباتی از بانک j  دارد. علاوه بر این مطالبات، هر بانک دارای یک دارایی خارجی (مانند سرمایه‌گذاری در بازار مسکن یا بورس) و یک شوک نقدینگی ϵi است.

منطق بازپرداخت و غیرخطی بودن:

تفاوت اساسی این مدل با مدل‌های قبلی در نحوه رفتار بانک هنگام مواجهه با بحران است. جریان وجوه نقد یک بانک(ci) حاصل‌جمع دارایی‌های خارجی، شوک‌های وارده و مبالغی است که از سایر بانک‌ها دریافت می‌کند. در اینجا سه سناریو رخ می‌دهد:

۱. وضعیت عادی: اگر جریان نقد بانک کافی باشد، تمام بدهی خود را به دیگران می‌پردازد.

۲. وضعیت نکول: اگر جریان نقد کمتر از بدهی باشد، بانک ورشکست شده و دارایی باقی‌مانده را به نسبت طلب بین طلبکاران تقسیم می‌کند .

۳. ورشکستگی کامل: اگر دارایی منفی شود، طلبکاران هیچ‌چیزی دریافت نمی‌کنند.

این رفتار باعث می‌شود تابع تعامل f  در اینجا به یک تابع پله‌ای یا غیرخطی تبدیل شود:

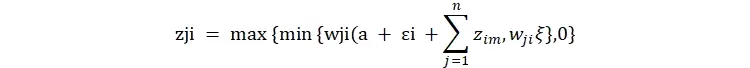
این معادله نشان می‌دهد که در سیستم‌های مالی، تعاملات فقط یک انتقال ساده نیست؛ بلکه یک آستانه وجود دارد. تا زمانی که شوک‌ها کوچک هستند، شبکه پایدار می‌ماند، اما به محض اینکه شوک از آستانه تحمل بانک عبور کند، «نکول» رخ می‌دهد و این ناتوانی در پرداخت، مانند یک دومینو به گره‌های بعدی منتقل می‌شود. آیا در چنین شبکه‌های پیچیده‌ای، همیشه به یک نقطه تعادل می‌رسیم؟

آن‌ها نشان می‌دهند که تحت فرضیات منطقی (مانند انقباضی بودن تابع تعامل)، همیشه یک تعادل وجود دارد و به طور کلی این تعادل یکتا است.

نکته ظریف اینجاست که در مدل‌های مالی (به دلیل غیرخطی بودن)، ممکن است چندین تعادل وجود داشته باشد، اما نویسندگان اثبات می‌کنند که حتی در آنجا هم تعادل در اکثر مواقع (Generically) یکتاست؛ یعنی احتمال بروز چندین تعادل پایدار در دنیای واقعی بسیار کم است.

حالا که مدل ساخته شد، نویسندگان به سراغ تحلیل حساسیت می‌روند: اگر به عاملr  شوک وارد شود، وضعیت کل اقتصاد چقدر تغییر می‌کند؟

در اقتصادهای «نرم» (که توابع در آن‌ها مشتق‌پذیر هستند)، برای تحلیل اثر شوک‌های کوچک، از تقریب مرتبه اول (بسط تیلور) استفاده می‌شود. نتیجه این تحلیل، ما را به مفهوم کلیدی ماتریس لئونتیف L می‌رساند:

L = (I - α W) ^ -1

این ماتریس، قلب تپنده تحلیل شبکه است. در اینجا α نشان‌دهنده قدرت تعاملات است. ماتریس لئونتیف به ما می‌گوید که اثر یک شوک بر عامل i  فقط ناشی از همسایگان مستقیمش نیست، بلکه از تمام مسیرهای موجود در شبکه عبور می‌کند:

L = I + α *W + α^2*W^2 +  α^3*W^3 + ………

در این رابطه:

•  I اثر مستقیم شوک بر خود عامل است.W*α اثر شوک بر همسایگان مستقیم و α^2*W^2 اثر شوک بر همسایگانِ همسایگان  و این زنجیره تا بی‌نهایت ادامه می‌یابد.

 مرکزیت بوناچیچ: چه کسی در اقتصاد «مهم‌تر» است؟

در نهایت، عجم‌اوغلو از مفهوم مرکزیت بوناچیچ[7] برای شناسایی گره‌های استراتژیک استفاده می‌کند. وی ثابت می‌کند که در سیستم‌های خطی، درجه گره شاخص ناقصی  برای نقاط پر اهمیت است. به جای آن، مرکزیت بوناچیچ که نوعی مرکزیت بردار ویژه است، اهمیت گره را تعیین می‌کند. این شاخص نشان می‌دهد که یک گره نه فقط به خاطر تعداد یال‌های مستقیم، بلکه به خاطر قرارگیری در مجاورت سایر گره‌های مهم، دارای اهمیت است. از این رو مشابه page rank گوگل می‌باشد با این تفاوت که یشتر بر «انباشت» و «انعکاس» اثرات حاصل از شوک تمرکز دارد.

تعریف: مرکزیت بوناچیچِ عامل i که با vi  نشان داده می‌شود، مجموع اثراتی است که این عامل بر تمام اعضای دیگر شبکه (مستقیم و غیرمستقیم) می‌گذارد.

طبق قضیه ۲ مدل، اگر شوک‌های وارده کوچک باشند، تغییر در خروجی کل اقتصاد (y) دقیقاً با میانگین وزنی شوک‌ها برابر است، که وزن هر شوک همان مرکزیت بوناچیچ آن گره است:

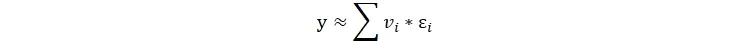
این فرمول به ما می‌گوید برای پیش‌بینی بحران‌های بزرگ، نباید فقط به میانگین شوک‌ها نگاه کرد. اگر یک شوک منفی کوچک به گره‌ای وارد شود که مرکزیت بوناچیچ بالایی دارد (یعنی در شبکه بسیار مرکزی است)، اثر آن بر اقتصاد کلان بسیار ویرانگرتر از شوک بزرگی است که به یک گره حاشیه‌ای وارد می‌شود.

اقتصادهای غیرنرم: مرز میان پایداری و فروپاشی

در دنیای واقعی، بسیاری از پدیده‌های اقتصادی دارای آستانه هستند. در یک اقتصاد غیرنرم، تابع تعامل f  در برخی نقاط مشتق‌ناپذیر است. این یعنی سیستم تا یک نقطه خاص در برابر فشار مقاومت می‌کند، اما به محض عبور از آن نقطه، رفتار سیستم به طور ناگهانی و جهشی تغییر می‌کند. مدل سرایت مالی که پیش‌تر ذکر شد، بهترین مثال برای اقتصاد غیرنرم است. یک بانک را در نظر بگیرید. تا زمانی که دارایی بانک مثبت است، او تمام تعهداتش را ایفا می‌کند (تغییرات خطی). اما به محض اینکه دارایی به صفر می‌رسد، بانک «نکول» می‌کند. در این لحظه، تابع بازپرداخت دچار یک شکستگی می‌شود.

این شکستگی به این معناست که یک شوک بسیار کوچک (مثلاً کاهش ۱ دلاری دارایی که منجر به منفی شدن تراز شود) می‌تواند ناگهان جریانی از بدهی‌های پرداخت‌نشده به ابعاد میلیون‌ها دلار را در شبکه به راه اندازد. در اینجا دیگر «تقریب تیلور» (که بر پایه مشتق است) کارایی ندارد، زیرا در نقطه شکست، مشتق تعریف نشده یا به بی‌نهایت میل می‌کند. برای ساده‌سازی ریاضی، می‌توان این توابع شکسته را با توابع نرمِ بسیار نزدیک به آن‌ها (Smooth Approximation) جایگزین کرد. او توضیح می‌دهد که اگر این تقریب را به درستی انجام دهیم، بینش‌های اقتصادی مدل (مانند نقش شبکه در انتشار بحران) تغییر نمی‌کند. این کار به ما اجازه می‌دهد هنوز از ابزارهایی مثل ماتریس لئونتیف استفاده کنیم، با این تفاوت که باید نسبت به «نقاط بحرانی» حساس باشیم.

در اقتصادهای غیرنرم، شبکه دیگر فقط یک «منتقل‌کننده» نیست، بلکه یک تقویت‌کننده است. ویژگی‌های کلیدی این وضعیت عبارتند از:

عدم تناسب: شوک‌های کوچک خرد می‌توانند منجر به نوسانات بزرگ کلان شوند.

شکنندگی سیستمیک: سیستم ممکن است در ظاهر پایدار به نظر برسد، اما در نزدیکی یک نقطه غیرنرم (مانند آستانه ورشکستگی بانک‌های بزرگ)، به شدت شکننده باشد.

تحلیل اقتصادهای غیرنرم به ما می‌گوید که چرا سیاست‌گذاران نباید صرفاً به میانگین‌ها و روندهای خطی دلخوش باشند. در شبکه‌های مالی، آنچه اهمیت دارد «فاصله تا آستانه نکول» در گره‌های مرکزی است. اگر شبکه غیرنرم باشد، یک جرقه کوچک در یک گره کلیدی می‌تواند کل گراف را به آتش بکشد، پدیده‌ای که در فیزیک به آن «تغییر فاز» و در اقتصاد به آن «بحران سیستمیک» می‌گوییم.

تا اینجا مشخص شد شوک‌های کوچک چگونه در شبکه پخش می‌شوند. اما سوال بعدی که اینجا مطرح می‌شود این است که قبل از اینکه بدانیم شوک به کدام گره وارد می‌شود، کدام ساختار شبکه برای کل جامعه امن‌تر است؟

او برای پاسخ به این سوال، «عملکرد کلان» را به صورت امید ریاضیِ وضعیت کلان تعریف می‌کند.

حالت الف -تقریب خطی (مرتبه اول: اولین نتیجه (نتیجه ۱) کمی نا امیدکننده است. در تقریب مرتبه اول (خطی)، مقدار انتظاری خروجی کل همیشه صفر است)(E[y1st]] = 0).  این یعنی در یک دنیای کاملاً خطی، مهم نیست شبکه چه شکلی باشد؛ چون فرض بر این است که شوک‌های مثبت و منفی همدیگر را خنثی می‌کنن و این همان چیزی بود که لوکاس فرض کرده بود. پس برای فهمیدن تفاوت شبکه‌ها، حتماً باید به سراغ تقریب مرتبه دوم (توابع غیرخطی) برویم. جایی که نظر لوکاس صدق نمی‌کند. حال اگر تابع کلان غیر خطی باشد دو حالت وجود دارد. بر حسب مشتق دوم تابع کلان که مثبت یا منفی است با دو حالت محدب و مقعر مواجه می‌شویم.

• اگر تابع  مقعر باشد: یعنی جامعه از نوسانات و ریسک بیزار است. در این حالت، تلاطم زیاد، عملکرد اقتصاد را کاهش می‌دهد.

• اگر تابع کلان محدب باشد: یعنی تلاطم باعث بهبود عملکرد می‌شود (که در اقتصاد کمتر رایج است).

وی ثابت می‌کند که عملکرد اقتصاد به توزیع مرکزیت بوناچیچ بین گره‌ها بستگی دارد و مجموع مجذور مرکزیت‌ها با واریانس مرکزیت‌ها رابطه مستقیم دارد. یعنی هرچه توزیع قدرت (مرکزیت) در یک شبکه نابرابرتر باشد (واریانس بالا)، اقتصاد در برابر شوک‌ها آسیب‌پذیرتر و عملکرد آن کمتر خواهد بود. بدین ترتیب دو نوع ساختار کلی ستاره‌ای شکل و یا شبکه منظم برای گرافها تعریف می‌گردد که هرکدام به صورت زیر تحلیل می‌گردد.

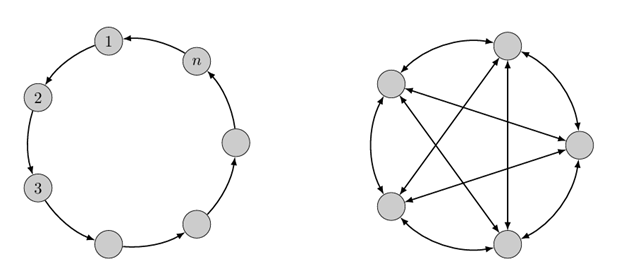
شبکه ستاره‌ای: در این شبکه نابرابری در اوج است. یک گره (مرکز) بسیار قدرتمند و بقیه ضعیف هستند. واریانس مرکزیت در اینجا بیشینه است. بنابراین، در یک اقتصاد با تابع تجمیع مقعر، شبکه ستاره‌ای بدترین عملکرد و بیشترین تلاطم را دارد. یک شوک به مرکز، کل سیستم را تکان می‌دهد و گره‌های دیگر نمی‌توانند آن را خنثی کنند.

شبکه منظم: شبکه‌هایی مانند «حلقوی» یا «کامل» که در آن هر گره تعداد یال‌های یکسانی دارد در این شبکه‌ها، همه گره‌ها مرکزیت بوناچیچ یکسانی دارند و واریانس مرکزیت صفر است. شبکه‌های منظم بهترین عملکرد را دارند. چون شوک‌ها به طور مساوی تقسیم می‌شوند و احتمال اینکه شوک‌های مثبت و منفی همدیگر را در کل شبکه خنثی کنند، در بالاترین حد خود است.

تعاملات غیرخطی: معمای پیوستگی شبکه

در بخش‌های قبلی، g که تابع کلان بود غیرخطی بود. حالا فرض می‌کنیم g  خطی است اما f یعنی تابع تعامل بین گره‌ها غیرخطی باشد. این یعنی «نحوه اثرگذاری گره‌ها بر یکدیگر» دارای تقعر یا تحدب است. عجم‌اوغلو نشان می‌دهد که انحنای تابع f  نشان‌دهنده بیزاری از ریسک در سطح خرد است. یعنی اگر مشتق دوم تابع تعامل منفی باشد سیستم تمایل دارد شوک‌ها را جذب و پخش کند (نیروهای تعدیل‌کننده) و اگر مثبت باشد یعنی سیستم تمایل دارد شوک‌ها را تقویت کند (نیروهای بحران‌زا).

سوال: در یک شبکه کامل، همه بانک‌ها یا بنگاه‌ها به طور مساوی به یکدیگر متصل هستند. آیا این همه اتصال خوب است؟ پاسخ عجم‌اوغلو شگفت‌انگیز است: بستگی دارد که کجای نمودار باشید!

۱. دنیای مقعر (امنیت در اتصال): وقتی تابع تعامل در اطراف نقطه تعادل، مقعر است. در این حالت، «شبکه کامل» بهترین عملکرد را دارد. چون شوک‌های وارده به یک گره، بین تمام گره‌های دیگر تقسیم و میرا می‌شود و هیچ‌کس آسیب جدی نمی‌بیند. (ایده Allen & Gale, 2000).

۲. دنیای محدب (خطر در اتصال):  ولی وقتی تابع تعامل تغییر شکل داده و در اطراف نقطه تعادل، محدب می‌شود. (مثل زمان رکود) در این حالت، «شبکه کامل» ناگهان به بدترین ساختار تبدیل می‌شود. چون حالا اتصالات زیاد مانند کانال‌هایی برای انتقال آتش عمل می‌کنند. یک جرقه کوچک در یک بانک، به جای پخش شدن، در بقیه بانک‌ها تقویت شده و منجر به «نکول زنجیره‌ای» می‌شود.

او  با این مدل، تناقض بین دو دیدگاه معروف را حل می‌کند:

• دیدگاه اول (Allen & Gale, 2000): اتصالات بیشتر مساوی ثبات بیشتر. (این در حالت مقعر درست است.)

• دیدگاه دوم (بحران‌های آبشاری): اتصالات بیشتر مساوی سرایت سریع‌تر بحران. (این در حالت محدب درست است.)

جمع‌بندی:

این پژوهش نشان داد که بسیاری از متغیرهای اقتصادی محصول ساختار شبکه‌ای اقتصاد هستند. برخلاف مدل‌های سنتی، شوک‌های قیمتی به‌صورت خطی پخش نمی‌شوند؛ بلکه از مسیرهای خاصی در زنجیره تأمین عبور کرده و در «هاب‌های صنعتی» تقویت یا تضعیف می‌شوند. بر اساس مدل عجم‌اوغلو و همکاران (2015)، در شبکه‌های نامتوازن، حتی شوک‌های خرد محلی نیز می‌توانند به دلیل روابط غیرخطی و حلقه‌های بازخورد، به بحران‌های سیستمیک و تورم کلان تبدیل شوند.

یافته‌های محوری تحقیق به شرح زیر است:

اهمیت توپولوژی شبکه: تاب‌آوری اقتصاد در برابر تورم بیش از آنکه به تنوع صنایع وابسته باشد، به نحوه اتصال آن‌ها بستگی دارد. شبکه‌هایی با ضریب خوشه‌بندی بالا، در انتقال منابع و اطلاعات سریع‌تر عمل می‌کنند، اما هم‌زمان می‌توانند کانالی برای سرایت سریع بحران باشند (Qiao & Ji, 2021).

پارادوکس پیچیدگی: در سطح بنگاه، افزایش بی‌رویه تعداد تأمین‌کنندگان (متوسط درجه بالا) لزوماً به معنای امنیت نیست، بلکه می‌تواند با افزایش هزینه‌های نظارتی، ارزش بازار شرکت را کاهش دهد؛ در حالی که «تناسب ساختاری» و فشردگی روابط، کلید حفظ ثبات مالی است(Orenstein & Zhang, 2023).

ناهمگنی زمانی و پویایی: فرآیند جایگزینی نهاده‌ها در صنایع زمان‌بر است (Goodwin, 1947). این تأخیرهای زمانی باعث می‌شود تورم به صورت «خوشه‌ای» و با رفتارهای غیرخطی ظاهر شود که تنها با ابزارهایی نظیر مرکزیت بوناچیچ قابل شناسایی است.

در نهایت، برای بومی‌سازی این رویکرد در ایران، انتقال از تحلیل‌های استاتیک لئونتیف به سمت مدل‌های شبکه‌ای داینامیک ضروری است. شناسایی صنایع گلوگاهی که شوک‌های قیمتی را به سایر بخش‌ها پمپاژ می‌کنند، مستلزم به‌روزرسانی جداول داده-ستانده و استفاده از آزمون‌های تنش برای پیش‌بینی مسیرهای سرایت تورم در ساختار اقتصادی کشور است.

مراجع  انگلیسی:

1.     Acemoglu, D., Akcigit, U., & Kerr, W. (2016). Networks and the Macroeconomy: An Empirical Exploration. In M. Eichenbaum & J. Parker (Eds.), NBER Macroeconomics Annual 2015, Volume 30 (pp. 273-335). University of Chicago Press

2.     Acemoglu, D., Ozdaglar, A., & Tahbaz-Salehi, A. (2015). Networks, shocks, and systemic risk. The Oxford Handbook of the Economics of Networks, 457-486. Oxford University Press.

3.     Afrouzi, H., & Bhattarai, S. (2023). Inflation and GDP dynamics in production networks: A sufficient statistics approach (NBER Working Paper No. 31218). National Bureau of Economic Research. https://doi.org/10.3386/w31218 (NBER)

4.     Allen, F., & Gale, D. (2000). Financial contagion. Journal of Political Economy, 108(1), 1-33. https://doi.org/10.1086/262109

5.     Bilgin, N. M. (2025). Inflation diffusion through production networks. ScienceDirect.
Duong, T. H., & Liu, W. (2025). The trade‑inflation nexus: The role of production networks [Manuscript]. SSRN.

6.     Bilgin, N. M. (2025). Inflation diffusion through supply chains. International Economics, 184, Article 100627. https://doi.org/10.1016/j.inteco.2025.100627 (OUCI)

7.     Goodwin, R. M. (1947). Dynamical coupling with especial reference to markets having production lags. Econometrica, 15(3), 181–204.

8.     Hirose, Y., Katayama, M., Ueda, K., & Watanabe, K. (2025). Inflation dynamics in production networks (CAMA Working Paper No. 22/2025). Centre for Applied Macroeconomic Analysis, Crawford School of Public Policy, The Australian National University. (IDEAS/RePEc)

9.     Leijonhufvud, A. (1997). Macroeconomics and complexity: Inflation theory. In B. Arthur, S. Durlauf, & D. Lane (Eds.), The economy as an evolving complex system II (Vol. 27). Addison-Wesley.

10.  Leontief, W. W. (1951). The structure of American economy, 1919–1939: An empirical application of equilibrium analysis (2nd ed.). Oxford University Press.

11.  Mantegna, R. N. (1999). Hierarchical structure in financial markets. The European Physical Journal B, 11(1), 193–197.

12.  Orenstein, P., & Zhang, R. (2023). How does supply network structure influence firms’ financial performance during disruption?. Entropy, 25(3), 430. https://doi.org/10.3390/e25030430

13.  Qiao, N., & Ji, C. (2021). Industry network structure determines regional economic resilience: An empirical study using stress testing. Sustainability, 13(3), 1146.

مراجع فارسی

مرکز آمار ایران.(۱۳۹۵). جدول داده–ستانده سال ۱۳۹۵. تهران: مرکز آمار ایران.

 [1] Mantegna

[2] Acemoglu

[3] Leontief

[4] Input-output linkage

[5] Supply and use

[6] Related Variety

[7] certainty equivalence

[8] یعنی همه بازیکنان از توابع سود یکدیگر و ساختار شبکه باخبرند.

[9] یعنی عوامل تولید دقیقا به شکل ضرب توانی باشند

[10] یعنی با دوبرابر شدن همه نهاده‌ها تولید هم دو برابر می‌شود

[11]توجه کنید فرض کردیم مصرف‌کننده «متقارن» است و بودجه‌اش را مساوی تقسیم می‌کند

[12] فرض گردیده است همه کالا فروش می‌رود و چیزی در انبار نمی‌ماند

[13] Bonacich Centrality