یادگیری ماشین به زبان من ( مرحله 16 - مدل SVM)

قضیه از چه قراره؟

پیدا کردن بهترین خط یا صفحه (Hyperplane) که داده‌ها رو از هم جدا کنه.

توضیح ریاضی

الگوریتم SVM:

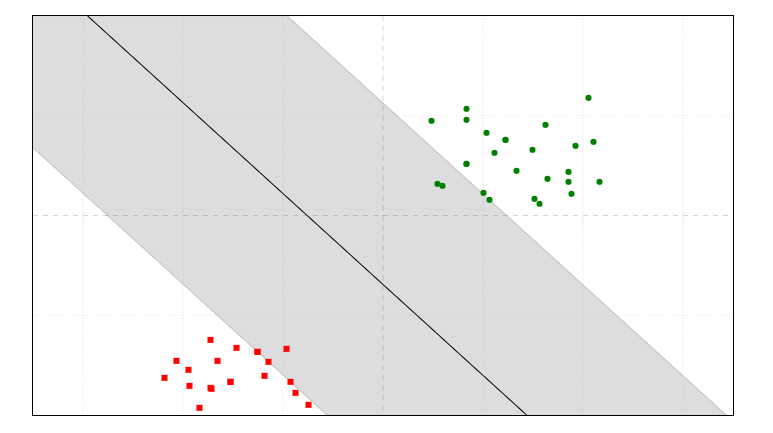
به تصویر بالا نگاه کنید :

دنباله خط سیاهی که کشیده شده رو SVM (Support Vector Machine) مینامند .

و فاصله بین خط و نزدیک ترین نقاط (بخش خاکستری ) رو Margin مینامند

برای درک بهتر این الگوریتم بشدت پیشنهاد میکنم بیاید وارد این وبسایت و خودتون بسازید و با اعدادش بازی کنید

https://greitemann.dev/svm-demo

بریم کد بزنیم , اول میخوام یک سری دیتا تولید کنم بعد باهم روش SVC انجام بدیم :

from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
import numpy as np
X, y = make_blobs(50, n_features=2, centers=2, random_state=40)
y = np.where(y == 0, -1, 1)
plt.scatter(X[:, 0], X[:, 1], c=y)
plt.show()

پیاده سازی SVC به صورت خطی :

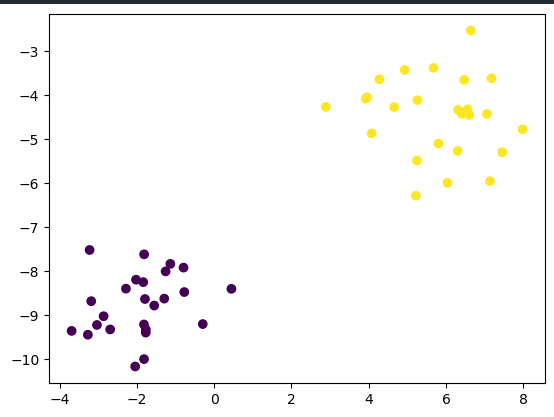
حالا میخوایم که به صورت خطی ( Linear SVM) جدا سازی رو انجام بدیم .

که فرمولش اینه :

w · x + b = 0

ما باید طوری w و b رو انتخاب کنیم که کمترین Margin رو داشته باشیم

yᵢ(w · xᵢ + b) ≥ 1

چند تا نقطه ای که لبه وکتور قرار دارند هم Support Vector گفته میشود .

حالا ما باید کدی بنویسیم که بهترین w و b رو به ما بده :

from sklearn.datasets import make_blobs
from sklearn.svm import SVC
import matplotlib.pyplot as plt

X, y = make_blobs(n_samples=100, centers=2, random_state=42)

model = SVC(kernel='linear', C=1)
model.fit(X, y)

plt.scatter(X[:, 0], X[:, 1], c=y, cmap='bwr')

w = model.coef_[0]
b = model.intercept_[0]

import numpy as np
x_vals = np.linspace(X[:, 0].min(), X[:, 0].max(), 100)
y_vals = -(w[0] * x_vals + b) / w[1]
plt.plot(x_vals, y_vals, 'k--')
plt.title("SVM with Linear Kernel")
plt.show()

حالا ما باید یک سری از پارامتر هایی که VC میگیره رو بدونیم چیه :

پارامتر اول Kernel .

کرنل چیست (Kernel) :

کرنل (Kernel) روشی هست برای اینکه بتونیم داده‌هایی که در فضای فعلی جداشدنی نیستند (مثلاً در ۲ بعد)، به یک فضای با بُعد بالاتر ببریم که در اونجا قابلیت جدا شدن داشته باشند.

برای مثال اینجا رو ببینید :

به تصویر بالا دقت کنید , داده ها به یک فضای ۲ بعدی رفته و سپس قابل جدا سازی شده اند , ما در SVM همین موارد رو داریم .

پس کرنل یک ترفند ریاضیه که کمک می‌کنه بدون اینکه واقعاً داده‌ها رو به فضای جدید ببریم، بتونیم اثر اون انتقال رو حساب کنیم.

مثال معروف: اگر داده‌ها در ۲ بعد دایره‌ای باشن و قابل جداسازی نباشن، با کرنل می‌تونیم اونا رو به فضای ۳ بعدی ببریم تا با یه صفحه (plane) جدا بشن.

ازتون دعوت میکنم این مقاله رو هم نگاهی بیندازید :

https://borisburkov.net/2021-08-03-1/

حالا در مثال SVC به چه صورته ؟

دوستان ما انواع کرنل رو داریم که مهم ترین اونها برای ما polynomial هستش در این مبحث که میاد داده‌ها رو با توان‌های مختلف به فضای بالاتر می‌بره (مثل x2,x3,...x^2, x^3, ...x2,x3,...) مثل تصویر زیر :

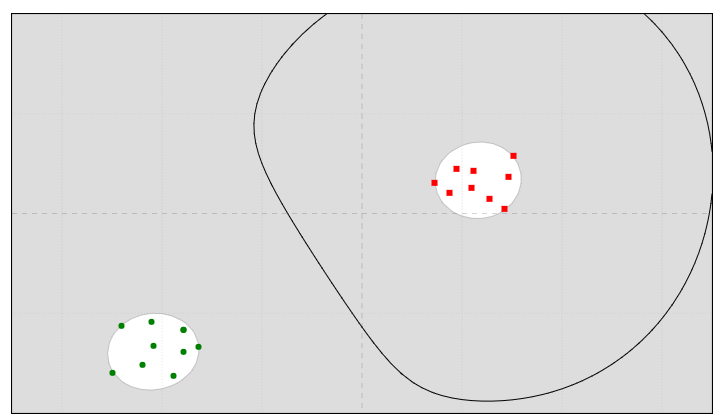
نیازی نیست حتما تو مبحث ریاضیاتی کرنل وارد بشید همین دید کلی رو داشته باشید . با کد به راحتی قابل پیاده سازی خواهد بود .

پارامتر بعدی که SVC میگیره گاما هستش برای کرنل های RBF .

این تابع می‌گه هر دو نمونه چقدر به هم نزدیکن (به صورت یک عدد بین ۰ و ۱).

from sklearn.svm import SVC
from sklearn.datasets import make_circles
import matplotlib.pyplot as plt
import numpy as np

X, y = make_circles(noise=0.1, factor=0.2, random_state=1)

for gamma in [0.1, 1, 10]:
    svc = SVC(kernel='rbf', gamma=gamma)
    svc.fit(X, y)    plt.title(f'gamma = {gamma}')
    plt.scatter(X[:, 0], X[:, 1], c=y)
    plt.show()

این بود کلیت مبحث SVC که امیدوارم مورد توجهتون قرار گرفته باشه .