بیتکوین: یک سیستم پول نقد الکترونیکی همتا به همتا
Satoshi Nakamoto
satoshin@gmx.com
این متن ترجمه فارسی «وایتپیپر بیتکوین» است که در سال ۲۰۰۸ توسط ساتوشی ناکاموتو منتشر شد. هدف از این ترجمه، دسترسی آسانتر فارسی زبانان به محتوای اصلی وایتپیپر بیتکوین است. متن حاضر ترجمهای است منطبق بر نسخه اصلی.

چکیده. نسخ های کاملاً همتا به همتا از پول الکترونیکی به ما این امکان رو میده که پرداختهای آنلاین رو مستقیماً از یک طرف به طرف دیگر بفرستیم بدون اینکه نیازی به عبور از یک موسسه مالی باشه. امضاهای دیجیتال بخشی از راه حل رو ارائه میدن، ولی مزایای اصلی از بین میرن اگر هنوز هم نیاز به یک طرف ثالث مورد اعتماد باشه تا از دوبار خرج کردن جلوگیری کنه. ما یک را ه حل برای مشکل دوبار خرج کردن ارائه میدیم با استفاده از یک شبکه همتا به همتا. این شبکه با هش کردن تراکنشها در یک زنجیره مداوم از اثبات کار مبتنی بر هش، تراکنشها را زمانبندی میکند و یک رکوردی رو شکل میده که نمیشه بدون دوباره انجام دادن اثبات کار تغییر داد. طولان یترین زنجیره نه تنها به عنوان مدرکی برای توالی رویدادهایی که شاهدش بودیم عمل میکنه، بلکه مدرکیه که نشون میده از بزرگترین مجموعه قدرت پردازشی CPU اومده. تا زمانی که اکثریت قدرت پردازشی CPU تحت کنترل گر ههایی باشه که برای حمله به شبکه همکاری نمیکنن، آنها طولانیترین زنجیره رو تولید میکنن و از حمل هکنندگان جلومیزنن. خود شبکه به حداقل ساختار نیاز داره.
پیامها به بهترین شکل ممکن پخش میشن، و گره ها میتونن از شبکه خارج و دوباره به آن بپیوندن به دلخواه، طولانیترین زنجیره کار رو به عنوان مدرک اینکه چی اتفاق افتاده وقتی آنها نبودند، قبول میکنند.
1. مقدمه
تجارت در اینترنت تقریباً به طور انحصاری به موسسات مالی به عنوان طر فهای ثالث مورد اعتماد برای پردازش پرداختهای الکترونیکی وابسته شده است. در حالی که این سیستم برای اکثر تراکنشها خوب کار م یکند، همچنان از ضعف های ذاتی مدل مبتنی بر اعتماد رنج میبرد. تراکنشهای کاملاً غیرقابل برگشت واقعاً ممکن نیستند، چرا که موسسات مالی نمیتوانند از دخالت در اختلافات خودداری کنند. هزینه دخالت باعث افزایش هزینه تراکنشها میشود، اندازه حداقل تراکنش عملی را محدود میکند و امکان انجام تراکنشهای کوچک و اتفاقی را حذف م یکند، و هزینه گسترده تری در از دست دادن توانایی انجام پرداختهای غیرقابل برگشت برای خدمات غیرقابل برگشت وجود دارد. با امکان برگشت، نیاز به اعتماد گسترش مییابد. فروشندگان باید از مشتریان خود مراقب باشند، آنها را برای کسب اطلاعات بیشتر از آنچه واقعاً نیاز دارند، آزار دهند. درصد مشخصی از تقلب به عنوان اجتنابناپذیر پذیرفته میشود. این هزینه ها و عدم قطعی تهای پرداخت میتوانند به صورت حضوری با استفاده از پول فیزیکی اجتناب شوند، اما هیچ مکانیزمی برای انجام پرداختها از طریق یک کانال ارتباطی بدون طرف ثالث مورد اعتماد وجود ندارد.
آنچه نیاز است یک سیستم پرداخت الکترونیکی مبتنی بر اثبات رمزنگاری به جای اعتماد است، که به هر دو طرف مایل اجازه میدهد مستقیماً با یکدیگر معامله کنند بدون نیاز به طرف ثالث مورد اعتماد.
میتوان از تراکنشهایی که از نظر محاسباتی عملاً غیرقابل برگشت هستند برای محافظت از فروشندگان در برابر تقلب استفاده کرد، و مکانیزم های اسکرو معمولی به راحتی میتوانند برای حفاظت از خریداران پیاد هسازی شوند. در این مقاله، ما یک راه حل برای مشکل دوبار خرج کردن با استفاده از یک سرور زما نبندی توزی عشده همتا به همتا پیشنهاد میکنیم تا اثبات محاسباتی ترتیب زمانی تراکنشها را تولید کند. سیستم تا زمانی که گر ههای صادق به صورت جمعی بیشتر از قدرت پردازشی CPU را نسبت به هر گروهی از گر ههای مهاجم که با هم همکاری میکنند، کنترل کنند، امن است.
2. تراکنشها
ما یک سکه الکترونیکی را به عنوان یک زنجیره از امضاهای دیجیتال تعریف میکنیم. هر صاحب سکه، آن را به صاحب بعدی منتقل میکند با امضای دیجیتالی هش تراکنش قبلی و کلید عمومی صاحب بعدی و اضافه کردن اینها به انتهای سکه. یک گیرنده میتواند امضاها را بررسی کند تا زنجیره مالکیت را تایید کند.
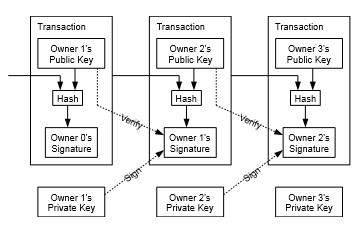
البته مشکل اینجاست که گیرنده نمیتواند تایید کند که یکی از صاحبان سکه آن را دوبار خرج نکرده است. یک راه حل معمول معرفی یک مرجع مرکزی مورد اعتماد، یا ضرابخانه، است که هر تراکنش را برای دوبار خرج کردن بررسی میکند. پس از هر تراکنش، باید سکه را به ضرابخانه برگرداند تا یک سکه جدید صادر کند، و تنها سکه هایی که مستقیماً از ضرابخانه صادر شد هاند، مورد اعتماد هستند که دوبار خرج نشده اند. مشکل این راه حل این است که سرنوشت کل سیستم پولی به شرکتی که ضرابخانه را اداره میکند، بستگی دارد، با هر تراکنشی که باید از طریق آنها انجام شود، دقیقاً مانند یک بانک.
ما به روشی نیاز داریم تا گیرنده بداند که صاحبان قبلی هیچ تراکنش زودتری را امضا نکرد هاند. برای مقاصد ما، اولین تراکنش مهم است، پس ما اهمیتی به تلا شهای بعدی برای دوبار خرج کردن نمیدهیم.”“تنها راه تایید نبود یک تراکنش، آگاهی از تمام تراکن شها است.در مدل مبتنی بر ضرابخانه، ضرابخانه از تمام تراکن شها آگاه بود و تصمیم میگرفت کدام یک اول رسیده است. برای انجام این کار بدون یک طرف مورد اعتماد، باید تراکنشها به صورت عمومی اعلام شوند] 1[، و ما به یک سیستم برای توافق شرکت کنندگان بر روی یک تاریخچه واحد از ترتیبی که دریافت شده اند نیاز داریم. گیرنده به مدرکی نیاز دارد که در زمان هر تراکنش، اکثریت گر هها موافق بودند که این اولین دریافت شده است.
3. سرور زمانبندی
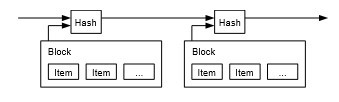
راهحلی که ما پیشنهاد م یکنیم با یک سرور زما نبندی شروع میشود. یک سرور زما نبندی با گرفتن هش یک بلوک از آیت مهایی که قرار است زما نبندی شوند کار م یکند و هش را به طور گسترده منتشر م یکند، مثلاً در یک روزنامه یا پست Usenet ]2-5[. زمانبندی اثبات میکند که داد هها باید در آن زمان وجود داشته باشند ،طبیعتاً، تا بتوانند در هش قرار گیرند. هر زما نبندی هش زمانبندی قبلی را در خود شامل م یشود، یک زنجیره ایجاد م یکند، و هر زما نبندی اضافی، زمانبندی های قبلی را تقویت میکند.
4. اثبات کار
برای پیاده سازی یک سرور زمانبندی توزیع شده بر پایه همتا به همتا، ما باید از یک سیستم اثبات کار استفاده کنیم که شبیه به Hashcash آدام بک] 6[ است، به جای استفاده از روزنامه ها یا پستهای Usenet. اثبات کار شامل جستجو برای یک مقدار است که وقتی هش میشود، مثلاً با 256-SHA، هش با تعدادی بیت صفر شروع میشود. میانگین کار مورد نیاز به صورت نمایی در تعداد بیت های صفر مورد نیاز است و م یتوان با اجرای یک هش تایید کرد.
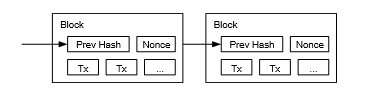
برای شبکه زما نبندی ما، ما اثبات کار را با افزایش یک nonce در بلوک تا زمانی که یک مقدار پیدا شود که هش بلوک را با بی تهای صفر مورد نیاز بدهد، پیاد هسازی م یکنیم. زمانی که تلاش CPU صرف شده است تا آن را مطابق با اثبات کار کند، بلوک نمیتواند بدون انجام دوباره کار تغییر کند. وقتی بلوک های بعدی پس از آن به زنجیر کشیده میشوند، کار برای تغییر بلوک شامل انجام دوباره تمام بلوک های پس از آن خواهد بود.
اثبات کار همچنین مشکل تعیین نمایندگی در تصمیم گیری اکثریت را حل میکند. اگر اکثریت بر اساس یک -آدرس-IP-یک-رای بود، توسط هر کسی که قادر به اختصاص دادن تعداد زیادی IP باشد، میتوانست دستکاری شود. اثبات کار در واقع یک -CPU-یک-رای است. تصمیم اکثریت توسط طولانی ترین زنجیره نمایندگی میشود، که بیشترین تلاش اثبات کار در آن سرمایه گذاری شده است. اگر اکثریت قدرت CPU تحت کنترل گر ه های صادق باشد، زنجیره صادق سریعتر رشد میکند و از هر زنجیره رقابتی جلو میزند. برای تغییر یک بلوک گذشته، یک مهاجم باید اثبات کار بلوک و تمام بلوک های پس از آن را دوباره انجام دهد و سپس با کار گر ه های صادق به روز شود و از آنها پیشی بگیرد. ما بعداً نشان خواهیم داد که احتمال یک مهاجم کندتر که سعی در رسیدن دارد، با اضافه شدن بلو کهای بعدی به طور نمایی کاهش مییابد.
برای جبران افزایش سرعت سختافزار و تغییر علاقه به اجرای گره ها در طول زمان، دشواری اثبات کار توسط یک میانگین متحرک تعیین میشود که هدف آن تعداد متوسط بلوک ها در هر ساعت است. اگر بیش از حد سریع تولید شوند، دشواری افزایش مییابد.
5. شبکه
مراحل اجرای شبکه به شرح زیر است:
۱. تراکنشهای جدید به تمام گره ها پخش میشوند.
۲. هر گره تراکنشهای جدید را در یک بلوک جمع آوری میکند.
۳. هر گره بر روی یافتن یک اثبات کار دشوار برای بلوک خود کار میکند.
۴. وقتی یک گره اثبات کار را پیدا میکند، بلوک را به تمام گره ها پخش میکند.
۵. گره ها بلوک را فقط در صورتی قبول میکنند که تمام تراکنشهای موجود در آن معتبر باشند و قبلاً خرج نشده باشند.
۶. گره ها با کار کردن بر روی ایجاد بلوک بعدی در زنجیره، موافقت خود را با بلوک ابراز میکنند، با استفاده از هش بلوک پذیرفت هشده به عنوان هش قبلی.
گر هها همیشه طولان یترین زنجیره را درست تلقی میکنند و بر روی گسترش آن کار میکنند. اگر دو گره نسخ ههای مختلفی از بلوک بعدی را همزمان پخش کنند، برخی گر هها ممکن است اول یکی را دریافت کنند. در این حالت، آنها بر روی اولینی که دریافت کرده اند کار میکنند، اما شاخه دیگر را در صورتی که طولانی تر شود، ذخیره میکنند. تساوی وقتی شکسته میشود که اثبات کار بعدی پیدا شود و یک شاخه طولانی تر شود؛ گر ههایی که بر روی شاخه دیگر کار می کردند، سپس به شاخه طولان یتر تغییر مسیر می دهند.
پخش تراکنشهای جدید لزوماً نیازی به رسیدن به تمام گره ها ندارد. تا زمانی که به تعداد زیادی از گره ها برسند، به زودی در یک بلوک قرار خواهند گرفت. پخش بلو کها نیز نسبت به پیا مهای از دست رفته تحمل پذیر است. اگر یک گره بلوکی را دریافت نکند، هنگامی که بلوک بعدی را دریافت کند و متوجه شود یکی را از دست داده است، آن را درخواست خواهد کرد.
6. انگیزه
به طور سنتی، اولین تراکنش در یک بلوک یک تراکنش ویژه است که یک سکه جدید را شروع م یکند که متعلق به خالق بلوک است. این امر انگیز های برای گر هها برای حمایت از شبکه فراهم میکند، و راهی برای توزیع اولیه سک هها در گردش ارائه میدهد، چون هیچ مرجع مرکزی برای صدور آنها وجود ندارد. اضافه شدن مداوم یک مقدار ثابت از سکه ای جدید مشابه استخراج کنندگان طلا که منابع را برای افزودن طلا به گردش صرف میکنند. در مورد ما، زمان CPU و برق است که صرف میشود.
انگیزه همچنین میتواند با هزین ههای تراکنش تأمین مالی شود.
اگر مقدار خروجی یک تراکنش کمتر از مقدار ورودی آن باشد، اختلاف به عنوان هزینه تراکنش است که به مقدار انگیزه بلوکی که تراکنش را شامل م یشود، اضافه میشود. هنگامی که تعداد مشخصی از سک هها وارد گردش شوند، انگیزه میتواند کاملاً به هزینه های تراکنش تغییر یابد و کاملاً بدون تورم باشد .
انگیزه ممکن است به تشویق گره ها برای باقی ماندن صادق کمک کند. اگر یک مهاجم حریص بتواند قدرت CPU بیشتری نسبت به تمام گر ههای صادق جمع آوری کند، باید بین استفاده از آن برای کلاهبرداری از مردم با پس گرفتن پرداختهای خود، یا استفاده از آن برای تولید سکه های جدید انتخاب کند. او باید آن را سودآورتر بیابد که با قوانین بازی کند، قوانینی که به او با سک ههای جدید بیشتر از همه دیگران به صورت ترکیبی سود می برند، تا اینکه سیستم و اعتبار ثروت خودش را تضعیف کند.
7. بازیابی فضای دیسک
هنگامی که آخرین تراکنش در یک سکه زیر تعداد کافی بلوک ها دفن شود، تراکنش های خرجشده قبل از آن میتوانند برای صرفه جویی در فضای دیسک حذف شوند. برای تسهیل این کار بدون شکستن هش بلوک، تراکن شها در یک درخت مرکل] 7[]2[]5[ هش میشوند، با فقط ریشه آن که در هش بلوک گنجانده میشود .
بلو کهای قدیمی سپس میتوانند با قطع کردن شاخه های درخت فشرده شوند. هش های داخلی نیازی به ذخیره سازی ندارند.
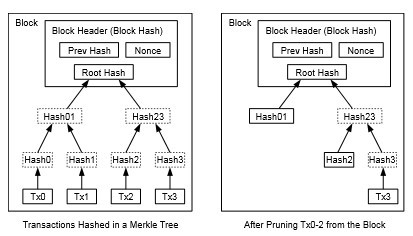
یک سربرگ بلوک بدون تراکنشها حدود ۸۰ بایت خواهد بود. اگر فرض کنیم بلو کها هر ۱۰ دقیقه تولید شوند ،۸۰ بایت ۶ ۲۴ * ۳۶۵ = ۴.۲ مگابایت در سال. با توجه به اینکه سیست مهای کامپیوتری معمولاً با ۲ گیگابایت رم در سال ۲۰۰۸ به فروش میرسند، و قانون مور پی شبینی رشد فعلی ۱.۲ گیگابایت در سال را میکند، ذخیره سازی نباید مشکلی باشد حتی اگر لازم باشد سربرگهای بلوک در حافظه نگه داشته شوند.
8. تایید پرداخت ساد هشده
امکان تایید پرداخ تها بدون اجرای یک گره کامل شبکه وجود دارد. یک کاربر فقط نیاز دارد یک نسخه از سربرگهای بلوک طولانی ترین زنجیره اثبات کار را نگه دارد، که م یتواند با پرس و جو از گره های شبکه تا زمانی که متقاعد شود طولانی ترین زنجیره را دارد، به دست آورد و شاخه مرکلی که تراکنش را به بلوکی که در آن زمانبندی شده است، متصل میکند. او نمیتواند خودش تراکنش را بررسی کند، اما با اتصال آن به جایی در زنجیره، م یتواند ببیند که یک گره شبکه آن را پذیرفته است، و بلو کهای اضافه شده پس از آن بیشتر تایید م یکنند که شبکه آن را پذیرفته است.
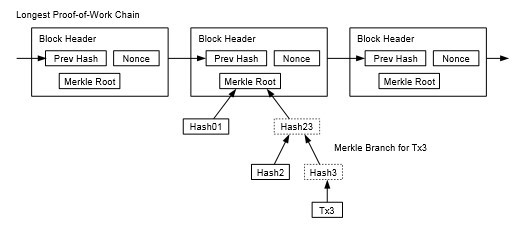
بنابراین، تایید تا زمانی که گرههای صادق شبکه را کنترل کنند، قابل اعتماد است، اما بیشتر آسیب پذیر است اگر شبکه توسط یک مهاجم زیر سلطه قرار گیرد. در حالی که گره های شبکه میتوانند خودشان تراکنشها را تایید کنند، روش ساد هشده میتواند توسط تراکن شهای ساختگی یک مهاجم فریب داده شود تا زمانی که مهاجم بتواند شبکه را زیر سلطه خود نگه دارد. یک استراتژی برای محافظت در برابر این موضوع این خواهد بود که از هشدارهای گره های شبکه وقتی یک بلوک نامعتبر را تشخیص میدهند، استفاده کنید، که باعث میشود نر مافزار کاربر بلوک کامل و تراکن شهای هشدارداد هشده را برای تایید ناسازگاری دانلود کند. کسبوکارهایی که پرداختهای مکرر دریافت میکنند، احتمالاً همچنان میخواهند گره های خودشان را برای امنیت مستقل تر و تایید سریع تر اجرا کنند.
9. ترکیب و تقسیم ارزش
اگرچه ممکن است تک تک سکه ها را به صورت جداگانه کنترل کرد، اما انجام یک تراکنش جداگانه برای هر سنت در یک انتقال دشوار خواهد بود. برای اجازه دادن به تقسیم و ترکیب ارزش، تراکنشها شامل ورود یها و خروجی های متعدد هستند. معمولاً یا یک ورودی واحد از یک تراکنش بزرگتر قبلی وجود دارد یا ورود یهای متعددی که مقادیر کوچکتر را ترکیب میکنند، و حداکثر دو خروجی: یکی برای پرداخت، و دیگری برای بازگرداندن باق یمانده، اگر وجود داشته باشد، به فرستنده.
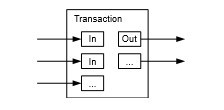
باید توجه داشت که فناوت، جایی که یک تراکنش به چندین تراکنش وابسته است و آن تراکنشها به بسیاری دیگر وابسته هستند، در اینجا مشکلی ایجاد نمیکند. هرگز نیازی به استخراج یک نسخه مستقل و کامل از تاریخچه یک تراکنش نیست.
10. حریم خصوصی
مدل بانکداری سنتی با محدود کردن دسترسی به اطلاعات به طر فهای درگیر و طرف ثالث مورد اعتماد، سطحی از حریم خصوصی را به دست می آورد. ضرورت اعلام عمومی تمام تراکنشها این روش را غیرممکن میکند، اما حریم خصوصی همچنان میتواند با قطع جریان اطلاعات در جای دیگر حفظ شود: با نگه داشتن کلیدهای عمومی به صورت ناشناس. عموم مردم میتوانند ببینند که کسی مقداری را به شخص دیگری میفرستد، اما بدون اطلاعاتی که تراکنش را به کسی مرتبط کند. این مشابه سطح اطلاعات منتشر شده توسط بورسهای اوراق بهادار است، جایی که زمان و اندازه معاملات فردی، “نوار”، عمومی میشود، اما بدون اینکه بگوید طرف ها چه کسانی بودند.
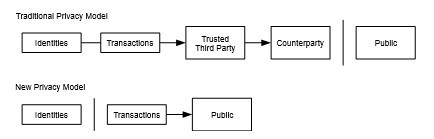
به عنوان یک دیوار آتش اضافی، باید برای هر تراکنش از یک جفت کلید جدید استفاده شود تا جلوی ارتباط آنها با یک صاحب مشترک گرفته شود. برخی ارتباطات هنوز با تراکنش های چند ورودی، که لزوماً نشان میدهند ورود ی هایشان متعلق به یک صاحب واحد بود هاند، اجتناب ناپذیر است. خطر این است که اگر صاحب یک کلید فاش شود، ارتباط ممکن است تراکنش های دیگری را که متعلق به همان صاحب بودند، فاش کند.
10.محاسبات
ما سناریوی یک مهاجم را در نظر م یگیریم که سعی در تولید یک زنجیره جایگزین سریعتر از زنجیره صادق دارد. حتی اگر این کار انجام شود، سیستم را به تغییرات دلخواه باز نمیکند، مانند ایجاد ارزش از هوا یا گرفتن پولی که هرگز متعلق به مهاجم نبوده است. گر هها یک تراکنش نامعتبر را به عنوان پرداخت قبول نخواهند کرد، و گر ههای صادق هرگز یک بلوک حاوی آ نها را قبول نخواهند کرد. یک مهاجم فقط میتواند سعی کند یکی از تراکن شهای خود را تغییر دهد تا پولی را که اخیراً خرج کرده است، پس بگیرد.
مسابقه بین زنجیره صادق و زنجیره مهاجم میتواند به عنوان یک قدمزنی تصادفی باینومیال توصیف شود.
رویداد موفقیت، افزایش زنجیره صادق با یک بلوک است، که باعث افزایش برتری آن به+ ۱ میشود، و رویداد شکست، افزایش زنجیره مهاجم با یک بلوک است، که باعث کاهش فاصله به -۱ م یشود.
احتمال اینکه یک مهاجم از یک کسری داد هشده دست پیدا کند، مشابه مسئله ورشکستگی قمارباز است. فرض کنید یک قمارباز با اعتبار نامحدود از یک کسری شروع میکند و تعداد نامحدودی آزمایشها را برای رسیدن به تعادل انجام م یدهد. ما میتوانیم احتمال اینکه او هرگز به تعادل برسد، یا اینکه یک مهاجم هرگز به زنجیره صادق دست پیدا کند، به شرح زیر محاسبه کنیم] ۸[ :
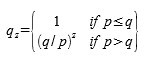
p = احتمال اینکه یک گره صادق بلوک بعدی را پیدا کن د q = احتمال اینکه مهاجم بلوک بعدی را پیدا کن د qz = احتمال اینکه مهاجم هرگز از z بلوک عق بافتاده دست پیدا کند.
با توجه به فرض ما که p > q است، احتمال به طور نمایی کاهش م ییابد به عنوان تعداد بلو کهایی که مهاجم باید به دست آورد، افزایش مییابد. با شانسه هایی که علیه او هستند، اگر او در ابتدا یک پیشروی خو ششانسانه نکند، شانسهای او به طور فزایندهای کوچک میشوند به عنوان اینکه او بیشتر عقب میماند.
حال ما در نظر م یگیریم که چقدر طول میکشد تا گیرنده یک تراکنش جدید قبل از اینکه به اندازه کافی مطمئن شود که فرستنده نمیتواند تراکنش را تغییر دهد، صبر کند. ما فرض میکنیم که فرستنده یک مهاجم است که میخواهد گیرنده را باور کند که او برای مدتی به او پرداخت کرده است، سپس آن را بعد از گذشت مدتی به خودش بازپرداخت میکند. گیرنده زمانی که این اتفاق بیفتد، هشدار میدهد، اما فرستنده امیدوار است که خیلی دیر شود.
گیرنده یک جفت کلید جدید تولید میکند و کلید عمومی را کمی قبل از امضا به فرستنده م یدهد. این از فرستنده جلوگیری میکند که یک زنجیره از بلو کها را از قبل آماده کند با کار کردن بر روی آن به طور مداوم تا زمانی که او به اندازه کافی خو ششانس باشد تا به اندازه کافی جلو برود، سپس در همان لحظه تراکنش را اجرا کند. وقتی تراکنش فرستاده میشود، فرستنده ناصادق به صورت مخفیانه بر روی یک زنجیره موازی شروع به کار م یکند که شامل نسخه جایگزین تراکنش خود است.
گیرنده منتظر م یماند تا تراکنش به یک بلوک اضافه شود و z بلو کها پس از آن به هم پیوند خورند. او مقدار دقیق پیشرفت مهاجم را نمیداند، اما با فرض اینکه بلوک های صادق زمان متوقع متوسط را به ازای هر بلوک گرفت هاند، پیشرفت بالقوه مهاجم یک توزیع پواسون خواهد بود با مقدار انتظاری:
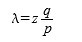
برای به دست آوردن احتمال اینکه مهاجم هنوز میتواند دست پیدا کند، ما چگالی پواسون را برای هر مقدار پیشرفتی که او میتوانسته انجام دهد، در احتمالی که او میتوانست از آن نقطه دست پیدا کند، ضرب میکنیم:
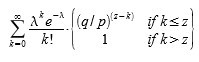
با تنظیم مجدد برای جلوگیری از جمع بندی دم بینهایت توزیع …
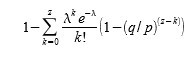
تبدیل به کد C.. .

با اجرای برخی نتایج، میتوانیم ببینیم که احتمال با z به طور نمایی کاهش مییابد.
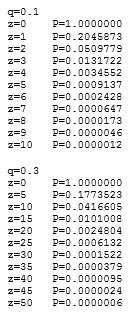
حل کردن برای P کمتر از ۰.۱% …

12. نتیجه گیری
ما یک سیستم برای تراکنش های الکترونیکی بدون تکیه بر اعتماد پیشنهاد کرده ایم. ما با چارچوب معمول سکه هایی که از امضاهای دیجیتالی ساخته شدهاند شروع کردیم، که کنترل قوی از مالکیت را فراهم میکند، اما بدون راهی برای جلوگیری از دوبار خرج کردن ناقص است. برای حل این مسئله، ما یک شبکه همتا به همتا را با استفاده از اثبات کار برای ثبت یک تاریخچه عمومی از تراکنشها پیشنهاد کردیم که به سرعت برای یک مهاجم تغییر دادن آن از نظر محاسباتی غیرعملی میشود اگر گره های صادق کنترل اکثریت قدرت CPU را داشته باشند. شبکه در سادگی بی ساختار خود مقاوم است. گره ها همه با هم با هماهنگی کمی کار میکنند. آ نها نیازی به شناسایی ندارند، چون پیام ها به هیچ جای خاصی مسیریابی نم یشوند و فقط نیاز است به بهترین شکل ممکن تحویل داده شوند. گره ها میتوانند به دلخواه از شبکه خارج شوند و دوباره به آن بپیوندند، زنجیره اثبات کار را به عنوان مدرکی از آنچه در غیابشان اتفاق افتاده است، پذیرفت هاند. آ نها با قدرت CPU خود رای می دهند، با پذیرش بلو کهای معتبر با کار کردن برای گسترش آ نها و رد کردن بلو کهای نامعتبر با خودداری از کار کردن روی آ نها، نظر خود را ابراز میکنند. هر قوانین و انگیز ههای مورد نیاز م یتوانند با این مکانیزم اجماع اجرا شوند.
محتوا های بیشتر در @BitTodayCrypto
یادداشت مترجم: این ترجمه توسط محمد مهدی مهرآئین انجام شده است. نسخه اصلی این وایتپیپر متعلق به ساتوشی ناکاموتو است. هدف از این کار صرفاً ارائه منبعی فارسی برای علاقهمندان و پژوهشگران حوزه بلاکچین و رمزارزهاست.
References
[1] W. Dai, "b-money," http://www.weidai.com/bmoney.txt, 1998.
[2] H. Massias, X.S. Avila, and J.-J. Quisquater, "Design of a secure timestamping service with minimal trust requirements," In 20th Symposium on Information Theory in the Benelux, May 1999.
[3] S. Haber, W.S. Stornetta, "How to time-stamp a digital document," In Journal of Cryptology, vol 3, no 2, pages 99-111, 1991.
[4] D. Bayer, S. Haber, W.S. Stornetta, "Improving the efficiency and reliability of digital time-stamping," In Sequences II: Methods in Communication, Security and Computer Science, pages 329-334, 1993.
[5] S. Haber, W.S. Stornetta, "Secure names for bit-strings," In Proceedings of the
4th ACM Conference on Computer and Communications Security, pages 28-35, April 1997.
[6] A. Back, "Hashcash - a denial of service counter-measure," http://www.hashcash.org/papers/hashcash.pdf, 2002.
[7] R.C. Merkle, "Protocols for public key cryptosystems," In Proc. 1980 Symposium on Security and Privacy, IEEE Computer Society, pages 122-133, April 1980.
[8] W. Feller, "An introduction to probability theory and its applications," 1957