دانیل گودوی 21 نوامبر 2018

اگر در حال آموزش یک طبقهبندیکننده دودویی هستید، به احتمال زیاد از آنتروپی متقاطع دودویی یا زیان لگاریتمی (binary cross-entropy / log loss) به عنوان تابع زیان استفاده میکنید. آیا تا به حال به این فکر کردهاید که استفاده از این تابع زیان دقیقاً به چه معناست؟ با توجه به سهولت استفاده از کتابخانهها و چارچوبهای امروزی، به راحتی ممکن است معنای واقعی تابع زیان مورد استفاده نادیده گرفته شود.
من به دنبال یک پست وبلاگی بودم که مفاهیم پشت آنتروپی متقاطع دودویی / زیان لگاریتمی را به شکلی بصری، واضح و مختصر توضیح دهد تا بتوانم آن را به دانشجویانم در دوره علوم داده نشان دهم. از آنجا که نتوانستم منبعی مناسب پیدا کنم، تصمیم گرفتم خودم این کار را انجام دهم.
بیایید با 10 نقطه تصادفی شروع کنیم:
x = [-2.2, -1.4, -0.8, 0.2, 0.4, 0.8, 1.2, 2.2, 2.9, 4.6]
این تنها ویژگی ماست: x.

اکنون، به نقاطمان رنگهایی اختصاص میدهیم: قرمز و سبز. اینها برچسبهای ما هستند.

بنابراین، مسئله طبقهبندی ما بسیار ساده است: با توجه به ویژگی x، باید برچسب آن را پیشبینی کنیم: قرمز یا سبز. از آنجا که این یک طبقهبندی دودویی است، میتوانیم مسئله را اینگونه نیز مطرح کنیم: «آیا نقطه سبز است؟» یا حتی بهتر، «احتمال سبز بودن نقطه چقدر است؟» در حالت ایدهآل، نقاط سبز باید احتمال 1.0 (برای سبز بودن) داشته باشند، در حالی که نقاط قرمز باید احتمال 0.0 (برای سبز بودن) داشته باشند. در این چارچوب، نقاط سبز به کلاس مثبت (بله، سبز هستند) تعلق دارند، در حالی که نقاط قرمز به کلاس منفی (خیر، سبز نیستند) تعلق دارند.
اگر مدلی را برای انجام این طبقهبندی آموزش دهیم، این مدل برای هر یک از نقاط، احتمالی برای سبز بودن پیشبینی میکند. با توجه به اطلاعاتی که درباره رنگ نقاط داریم، چگونه میتوانیم ارزیابی کنیم که احتمالات پیشبینیشده چقدر خوب (یا بد) هستند؟ این دقیقاً هدف تابع زیان است! تابع زیان باید برای پیشبینیهای بد مقادیر بالایی و برای پیشبینیهای خوب مقادیر پایینی برگرداند. برای یک طبقهبندی دودویی مثل مثال ما، تابع زیان معمول، آنتروپی متقاطع دودویی / زیان لگاریتمی است.
اگر این تابع زیان را جستجو کنید، با فرمول زیر مواجه خواهید شد:

آنتروپی متقاطع دودویی / زیان لگاریتمی که در آن y برچسب است (1 برای نقاط سبز و 0 برای نقاط قرمز) و p(y) احتمال پیشبینیشده سبز بودن نقطه برای تمام N نقطه است. با خواندن این فرمول، متوجه میشوید که برای هر نقطه سبز (y=1)، لگاریتم احتمال سبز بودن (log(p(y))) به زیان اضافه میشود. برعکس، برای هر نقطه قرمز (y=0)، لگاریتم احتمال قرمز بودن (log(1-p(y))) به زیان اضافه میشود. این فرمول خیلی پیچیده نیست، اما چندان شهودی هم به نظر نمیرسد.
علاوه بر این، آنتروپی چه ربطی به این موضوع دارد؟ چرا اصلاً از لگاریتم احتمالات استفاده میکنیم؟ اینها سؤالات درستی هستند و امیدوارم در بخش «ریاضیات را نشان بده» در ادامه به آنها پاسخ دهم. اما پیش از رفتن به سراغ فرمولهای بیشتر، اجازه دهید یک نمایش بصری از فرمول بالا به شما نشان دهم...
ابتدا، نقاط را بر اساس کلاسهایشان، مثبت یا منفی، جدا میکنیم، همانطور که در شکل زیر نشان داده شده است.
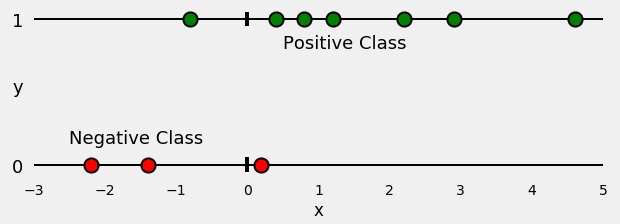
اکنون، یک رگرسیون لجستیک را برای طبقهبندی نقاطمان آموزش میدهیم. رگرسیون مناسبشده یک منحنی سیگموید است که احتمال سبز بودن یک نقطه را برای هر مقدار x نشان میدهد.به صورت زیر است:
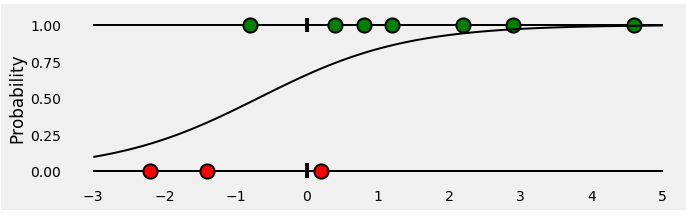
سپس، برای تمام نقاط متعلق به کلاس مثبت (سبز)، احتمالات پیشبینیشده توسط طبقهبندیکننده ما چیست؟ اینها میلههای سبز زیر منحنی سیگموید، در مختصات x مربوط به نقاط هستند.

تا اینجا همهچیز خوب است! اما نقاط متعلق به کلاس منفی چطور؟ به یاد داشته باشید، میلههای سبز زیر منحنی سیگموید نشاندهنده احتمال سبز بودن یک نقطه هستند. پس احتمال قرمز بودن یک نقطه چیست؟ البته میلههای قرمز بالای منحنی سیگموید!
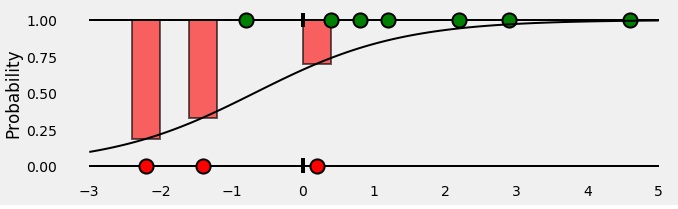
با کنار هم قرار دادن همه اینها، چیزی شبیه به این به دست میآید: میلهها نشاندهنده احتمالات پیشبینیشده مرتبط با کلاس واقعی هر نقطه هستند!

خب، حالا احتمالات پیشبینیشده را داریم... وقت آن است که با محاسبه آنتروپی متقاطع دودویی / زیان لگاریتمی آنها را ارزیابی کنیم! این احتمالات تنها چیزی هستند که نیاز داریم، پس بیایید محور x را حذف کنیم و میلهها را کنار هم قرار دهیم.

خب، میلههای آویزان دیگر معنایی ندارند، پس بیایید آنها را دوباره مرتب کنیم.

از آنجا که هدف ما محاسبه زیان است، باید پیشبینیهای بد را جریمه کنیم، درست است؟ اگر احتمال مرتبط با کلاس واقعی 1.0 باشد، زیان آن باید صفر باشد. برعکس، اگر این احتمال پایین باشد، مثلاً 0.01، زیان باید بسیار زیاد باشد!
معلوم میشود که گرفتن لگاریتم منفی احتمال برای این منظور به خوبی کار میکند (چون لگاریتم مقادیر بین 0.0 و 1.0 منفی است، ما لگاریتم منفی را میگیریم تا مقدار مثبتی برای زیان به دست آید).
در واقع، دلیل استفاده از لگاریتم به تعریف آنتروپی متقاطع برمیگردد، لطفاً برای جزئیات بیشتر بخش «ریاضیات را نشان بده» را در ادامه بررسی کنید.
نمودار زیر تصویر واضحی به ما میدهد - هرچه احتمال پیشبینیشده کلاس واقعی به صفر نزدیکتر شود، زیان به صورت نمایی افزایش مییابد.

عادلانه است! بیایید لگاریتم منفی احتمالات را بگیریم - اینها زیانهای مربوط به هر یک از نقاط هستند. در نهایت، میانگین تمام این زیانها را محاسبه میکنیم.

و تمام! ما با موفقیت آنتروپی متقاطع دودویی / زیان لگاریتمی این مثال ساده را محاسبه کردیم. مقدار آن 0.3329 است!
اگر میخواهید مقدار بهدستآمده را دوباره بررسی کنید، کافی است کد زیر را اجرا کنید و خودتان ببینید:
from sklearn.linear_model import LogisticRegression from sklearn.metrics import log_loss import numpy as np x = np.array([-2.2, -1.4, -.8, .2, .4, .8, 1.2, 2.2, 2.9, 4.6]) y = np.array([0.0, 0.0, 1.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0]) logr = LogisticRegression(solver='lbfgs') logr.fit(x.reshape(-1, 1), y) y_pred = logr.predict_proba(x.reshape(-1, 1))[:, 1].ravel() loss = log_loss(y, y_pred) print('x = {}'.format(x)) print('y = {}'.format(y)) print('p(y) = {}'.format(np.round(y_pred, 2))) print('Log Loss / Cross Entropy = {:.4f}'.format(loss))
جدا از شوخی، این پست قصد ندارد خیلی ریاضیمحور باشد... اما برای شما خوانندگانی که میخواهید نقش آنتروپی و لگاریتم را در این موضوع درک کنید، برویم جلو.
اگر میخواهید عمیقتر به نظریه اطلاعات، شامل آنتروپی، آنتروپی متقاطع و خیلی مفاهیم دیگر بپردازید، پست کریس اولا را ببینید؛ بسیار دقیق و کامل است!
بیایید با توزیع نقاطمان شروع کنیم. چون y نشاندهنده کلاسهای نقاط ماست (ما ۳ نقطه قرمز و ۷ نقطه سبز داریم)، توزیع آن، که آن را q(y) مینامیم، به این شکل است:

آنتروپی معیاری از عدم قطعیتی است که با یک توزیع معین q(y) همراه است.
اگر همه نقاطمان سبز بودند، عدم قطعیت آن توزیع چه میشد؟ صفر، درست است؟ چون هیچ شکی درباره رنگ یک نقطه وجود نداشت: همیشه سبز بود! پس آنتروپی صفر است!
از طرف دیگر، اگر دقیقاً نصف نقاط سبز و نصف دیگر قرمز بودند، این بدترین حالت ممکن است، نه؟ هیچ مزیتی در حدس زدن رنگ یک نقطه نداشتیم: کاملاً تصادفی بود! در این حالت، آنتروپی با فرمول زیر محاسبه میشود (ما دو کلاس داریم — قرمز یا سبز — پس پایه ۲):

برای هر حالت میانی دیگر، میتوانیم آنتروپی توزیع q(y) را با فرمول زیر محاسبه کنیم، که C تعداد کلاسهاست:
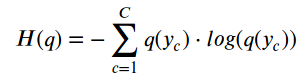
پس اگر توزیع واقعی یک متغیر تصادفی را بدانیم، میتوانیم آنتروپیاش را محاسبه کنیم. اما اگر اینطور باشد، چرا اصلاً زحمت آموزش یک طبقهبندیکننده را بکشیم؟ ما که توزیع واقعی را میدانیم...
اما اگر ندانیم چه؟ آیا میتوانیم توزیع واقعی را با توزیع دیگری، مثلاً p(y)، تقریب بزنیم؟ البته که میتوانیم!
فرض کنیم نقاطمان از توزیع دیگری p(y) پیروی میکنند. اما ما میدانیم که در واقع از توزیع واقعی (ناشناخته) q(y) میآیند، درست است؟
اگر آنتروپی را اینگونه محاسبه کنیم، در واقع داریم آنتروپی متقاطع بین دو توزیع را محاسبه میکنیم:

اگر به طور معجزهآسایی p(y) را کاملاً با q(y) منطبق کنیم، مقدار آنتروپی متقاطع و آنتروپی یکسان خواهد شد.
چون این تقریباً هرگز اتفاق نمیافتد، آنتروپی متقاطع مقداری بزرگتر از آنتروپی محاسبهشده روی توزیع واقعی خواهد داشت.
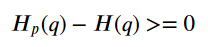
این تفاوت بین آنتروپی متقاطع و آنتروپی نامی دارد...
واگرایی کولبک-لیبلر یا به اختصار «واگرایی KL»، معیاری از ناهمسانی بین دو توزیع است:
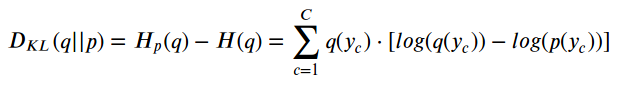
این یعنی هرچه p(y) به q(y) نزدیکتر شود، واگرایی و در نتیجه آنتروپی متقاطع کمتر خواهد شد.
پس باید یک p(y) خوب پیدا کنیم... اما این دقیقاً کاری نیست که طبقهبندیکننده ما باید انجام دهد؟! و واقعاً هم همین کار را میکند! به دنبال بهترین p(y) ممکن میگردد، یعنی آن که آنتروپی متقاطع را کمینه کند.
در طول آموزش، طبقهبندیکننده از هر یک از N نقطه در مجموعه آموزشی برای محاسبه زیان آنتروپی متقاطع استفاده میکند و در واقع توزیع p(y) را برازش میدهد! چون احتمال هر نقطه ۱/N است، آنتروپی متقاطع به این شکل میشود:

شکلهای ۶ تا ۱۰ را یادتان هست؟ ما باید آنتروپی متقاطع را روی احتمالات مربوط به کلاس واقعی هر نقطه محاسبه کنیم. یعنی استفاده از میلههای سبز برای نقاط کلاس مثبت (y=1) و میلههای قرمز آویزان برای نقاط کلاس منفی (y=0) یا به زبان ریاضی:

گام نهایی، محاسبه میانگین تمام نقاط در هر دو کلاس مثبت و منفی است:

در نهایت، با کمی دستکاری، میتوانیم هر نقطهای را، چه از کلاس مثبت و چه منفی، زیر یک فرمول واحد بیاوریم:

و تمام! دوباره به فرمول اصلی آنتروپی متقاطع دودویی / زیان لگاریتمی رسیدیم.
واقعاً امیدوارم این پست توانسته باشد نور تازهای بر مفهومی بیندازد که اغلب بدون توجه پذیرفته میشود، یعنی آنتروپی متقاطع دودویی به عنوان تابع زیان. همچنین امیدوارم کمی نشان داده باشد که یادگیری ماشین و نظریه اطلاعات چقدر به هم مرتبط هستند.