یک مسئله جالب در leetcode وجود داره که میخواد یک سطح مستطیلی رو با کمترین تعداد مربع پوشش بده. مسئله شماره ۱۲۴۰. اضلاع مربعهای انتخابی اعداد صحیح هستند. شاید اولین ایده قرار دادن بزرگترین مربع ممکن باشه به این شکل که عرض مستطیل اولیه میشه اولین مربع انتخابی بعد از فضای باقیمانده مربع بعدی رو انتخاب کنیم و به همین ترتیب جواب رو بدست بیاریم. پس تا اینجا با یک رویه بازگشتی سر و کار داریم. اما اگر آخرین مثال این مسئله رو نگاه کنید به راحتی متوجه میشید که این راه ما رو به جواب نمیرسونه. در نتیجه نیاز به بررسی تمام حالتهای ممکن داریم.
با توجه به محدودیتهای مسئله بزرگترین ضلع میتونه ۱۳ باشه پس همچنان ایده بازگشتی میتونه کارآمد باشه اما با کمی هرس! پس یعنی میتونیم از روش عقبگرد یا backtracking استفاده کنیم. چرا؟ چون ایده اولیه که از بزرگترین مربع ممکن که ضلعی برابر با عرض مستطیل داره هم چنان میتونه کارآمد باشه. شاید خود این حالت ما رو به جواب درست نرسونه اما میتونه شروع خوبی باشه!
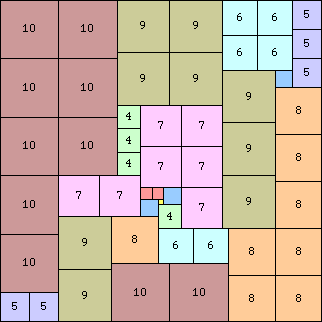
مثلا مثال اول رو در نظر بگیرید که مستطیل طولی برابر با ۱۳ و عرضی برابر با ۱۱ داره. اگر اولین مربع انتخابی به ضلع ۱۱ باشه٬ مستطیل باقیمانده ۲*۱۱ میشه که با پنج تا مربع ۲*۲ و دو مربع ۱*۱ کامل میشه اما همونطور که میبینید حداقل تعداد مربعها میتونه کمتر از ۷تا باشه :

همونطور که اشاره شد٬ این جواب درست نیست ولی میتونه ما رو به جواب درست برسونه. چرا؟ چون مربع بزرگتری نمیتونیم قرار بدیم پس باید حالتهای دیگه رو امتحان کنیم تا شاید جواب بهتری رو پیدا کنیم. در نتیجه روش ایده زدن ما به این صورته که نقطه شروع بزرگترین مربع ممکن و به ترتیب امتحان کردن مربعهای کوچکتر از اونه.
یعنی اول یه مربع به ضلع x رو انتخاب میکنم و اون رو قرار میدم. دقت کنید به یک روشی نیاز داریم که بتونیم این استیت رو نگه داریم. یعنی بدونیم با قرار دادن مربع x چه خونههایی از مستطیل اصلی پر شده و چه خونههایی خالیه.
دید کلی به این سوال بازگشتی بود. اما تعدادی از فراخوانیهای بازگشتی که انجام میشه نیازی به ادامه دادن ندارند. یعنی با حالتهای پایهای بهینهتر میتونیم درخت جستجوی حالتها رو هرس کنیم.
اما چطور باید حالتهای مختلف بررسی بشن؟
فکر کنید یک مورچه قرار دادین که خونههای مستطیل رو دونه دونه جلو می ره. اگر مستطیل رو یک ماتریس فرض کنید که دارای r ردیف و c ستون هست٬ اگر مورچه در ردیف r و ستون صفرم باشه در هر فراخوانی یک ستون به جلو میره تا زمانی که در ستون آخر قرار بگیره که در این صورت فراخوانی باید برای ردیف بعدی انجام بشه. همونطور که دقت کردید به یکی از base caseها یا حالت پایه اشاره شد.
در هر فراخوانی مختصات خاصی در نظر گرفته شده یعنی در یک فراخوانی چه ردیف و ستونی باید بررسی بشه. اگر در یک فراخوانی ردیف بزرگتر از r بشه به این معنیه که کار تمام شده و اگر جواب بهتری از قبلی بدست آوردیم آپدیت میکنیم.
اما چطور جوابها رو هرس میکنیم؟ مثلا بار اولی که میخوایم سوال رو برای m=13 و n=11 حل کنیم جواب ۷ بدست میاد. اما میدونیم که این بهترین جواب نیست. در هر صورت باید سایر جوابها رو کنترل کنیم تا بهترین جواب رو پیدا کنیم. فرض کنید شما واقعا مربع های گوناگونی دارید که میتونید با اونها این مستطیل رو پر کنید. وقتی یک راه حل پیدا کردید٬ دوباره از آخرین مربع که قرار دادید شروع میکنید به برداشتن و چک کردن اینکه آیا این امکان وجود داشت که مربع دیگری قرار بدین؟
فرض کنید در حل همین حالت٬ شما از آخرین مربع 1*1 شروع کنید. اولی رو برمیدارید و مربع دیگری نمیتونید قرار بدید. به یک مرحله قبلتر برمیگردید و مربع 1*1 بعدی رو حذف میکنید باز به همین ترتیب. باز یک مرحله عقبتر برمیگردیم و به یک مربع 2*2 میرسیم. اگه مربع 2*2 رو حذف کنم٬ چه مربعی میتونم قرار بدم؟ میتونم این فضا رو با چهار مربع 1*1 پر کنم اما اینکه بدتر شد! پس زمان این فراخوانی میدونم که تعداد جوابهای فعلیم بیشتر از ۷ شده٬ در نتیجه این مسیر رو ادامه نمیدم و باید تعداد مرحله بیشتری به عقب برگردم. همین روند برای دو مربع 2*2 دیگه تکرار میشه. میرسیم به مربع ۱۱*۱۱ . با حذف این مربع میشه یک مربع 10*10 قرار داد. اما خب همونطور که مشاهده میشه تعداد مربعهای بیشتری از بهترین جواب فعلی بدست اومده. البته همونطور که اشاره شد٬ هرس اتفاق میفته و نمیذاره مورچه این راه اشتباه رو تا آخر ادامه بده و بعد پشیمون شه!

بلکه در اولین فراخوانی که تعداد جواب از ۷ بیشتر شده از این راه صرف نظر میکنه و برمیگرده عقب. (میتونین فکر کنین چطور برمیگرده عقب و در حین قرار دادن کدوم مربع این تصمیم رو میگیره؟) مشابه حالت قبلی دوباره میرسه به مربع 11*11 و با حذف اون مربع ۱۰ رو انتخاب میکنه. همین روال تکرار میشه و میتونین این حالت رو روی کاغذ بکشید و ببینید که بازم جواب بهتری بدست نمیاد. به همین شکل ادامه میده تا به مربع ۷ میرسه و جواب کمتری از جواب قبلی بدست میاره.
اگه با توضیحات بالا متوجه روش عقبگرد نشدید حتما تو کامنتها عنوان کنید تا با مثالهای سادهتری توضیح بدم. همچنین کشیدن درخت این مثال خیلی مفصل میشه اما میشه برای سوالهای سادهتر٬ برای فهم بهتر عقبگرد رو روی درخت تصمیم نمایش داد. حالا شاید بپرسید چرا این مثال رو انتخاب کردم که عددهای بزرگی داره نسبتا چون تو این مثال هست که شما نقض انتخاب بزرگترین مربع ممکن بعنوان جواب کارآمد رو میبینید.
توضیحات تکمیلی:
دقت داشته باشید که در هر فراخوانی ما خونه به خونه جلو میریم و برای کاهش تعداد فراخوانیها میتونیم به جای یک خونه جلو رفتن kتا خونه به جلو بریم و k ضلع مربعی هست که انتخاب شده تا در این مرحله مستطیل رو پوشش بده. این حرکت و هرس کردن حالتهایی که بیشتر از جواب فعلی میشن و ادامه ندادن اونها٬ مثالهای از بهینه سازی این راه حله. اما یک کار دیگه هم میشه کرد که من فقط عنوان میکنم و اگر فکر کردید نیازه تو کامنتها بگید توضیح بدم. اینکه میشه به جای نگه داشتن یک ماتریس Boolean برای فهمیدن اینکه چه خونهای قبلا پر شده میشه از یک آرایه به طول ردیفهامون استفاده کرد و استیت رو به شکل یک bitmask نگهداری کرد. به این ترتیب در هر ردیف تعدادی از ستونهای اون ردیف پر هستند و تعداد خالی. مثلا اگر ۴ ردیف و ۵ ستون داشته باشیم و یک مربع ۳*۳ رو طوری قرار بدیم که گوشه بالا و چپ روی (0,0) ماتریس باشه٬ ردیفهای صفرم٬ اول و دوم تعدادی ستون پر دارند. چه ستونهایی؟ ستونهای صفرم و اول و دوم پر هستند. [111,111,111,000] یعنی ردیف صفرم٬ اول و دوم سه ستون پر دارند و ردیف سوم هیچ ستون پری نداره.