

سلام!
ازت میخوام این موقعیت رو تصور کنی. یه شهر که یک آرایشگر خاص داره. این آرایشگر تمام کسایی که داخل اون شهر هستند و خودشون رو اصلاح نمیکنند رو اصلاح میکنه. در واقع میگیم مشتریان این آرایشگر خوداصلاحکن نیستن.
دقت کن که این آرایشگر کسانی که خوداصلاحکن هستن رو نمیتونه اصلاح کنه.
حالا به نظرت این آرایشگر، خودش رو هم اصلاح میکنه یا نه؟
حالا یه سوال دیگه!
یه محقق رو تصور کنید که قصد داره یک کتاب شامل اسم تمام نویسندههایی که اسمشون رو در کتابشون ذکر نکردن، گردآوری کنه. ولی یه سوال براش پیش اومده.
آیا این شخص باید اسم خودش رو در این کتاب بیاره؟
عجب سوالات گیجکنندهای!
تو چه جوابی برای این دو سوال داری؟

قبل از جواب دادن به سوالهای اپیزود قبلی، بریم ببینیم این مسائل تو منطق ریاضیاتی چطوری مدل میشه؟
مثالهایی که در اپیزود قبلی بهش اشاره کردیم، یک بیانی از پارادوکس راسل هستند.
پارادوکس راسل چی هست ؟
پارادوکس راسل روی منطق و نظریهی مجموعهها بیان میشه به این شکل که فرض کن میخوایم یک مجموعه R بسازیم به طوری که R شامل همه مجموعههایی هست که خودشون عضو خودشون نیستن! یا به طور ریاضیاتی:
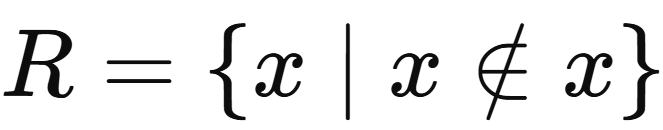
حالا نگاه کن که تعریف این مجموعه چطوری به تناقض منجر میشه:
پس:

برگردیم به مسئلهی آرایشگر، اول بیا فرض کنیم که جواب بلهست. این یعنی آرایشگر خودش رو اصلاح میکنه، پس اون یک خوداصلاحکنه. پس اینجا ما به یک تناقض میرسیم؛ چون گفتیم آرایشگر خوداصلاحکنها رو اصلاح نمیکنه پس نباید خودش رو هم اصلاح کنه!
حالا که نتیجه گرفتیم آرایشگر خودش رو اصلاح نمیکنه، دیگه یک خوداصلاحکن نیست. پس طبق قواعدی که برای اصلاح داشت باید همه کسایی که خوداصلاحکن نیستن رو اصلاح کنه، که در اینصورت باید خودش رو اصلاح کنه و دوباره تناقض!
حالا بریم سراغ مسئلهی کتاب، اگر اسم نویسنده در کتاب خودش باشه، پس دیگه نمیتونه در لیست باشه (چون کتاب فقط شامل اسم نویسندههاییه که اسمی ازشون در کتابشون ذکر نشده).
و اگر اسمش در کتابش نباشه، پس واجد شرایطه و باید اسمش در این کتاب خاص وجود داشته باشه.
این تناقض مشابه پارادوکس راسله که در آن تعریف مجموعه باعث خودارجاعی و در نتیجه تناقض میشه.
تو هم میتونی مثالی برای این پارادوکس بزنی؟

نتیجه حرفامون تا این جا اینه که
نظریهى طبیعى مجموعهها در قرن نوزدهـم بـه وسیلهی گئورگ کانتور پایهریزی شــد، نامبرده تــا اومد بــراى خودش غوغایی بـه پـا کنـه، تودهاى عظیم از پارادوکسها بود کــه بــه ســمتش روانـه شـد. البته کـه غوغا هم کرد، ولـى یـک غوغاى پارادوکسگونه!
حالا به نظرت نظریهپردازان مجموعهها چطوری این مشکل (پارادوکس راسل) رو حل کردند؟
برای رفع این تناقض، نظریهپردازان مجموعهها نظریههای مجموعهای جدیدتری مانند نظریه مجموعههای ZFC رو ارائه دادن که محدودیتهایی بر مجموعهها وضع میکرد. در این نظریهها، قوانینی مثل محدودیتهای خودارجاعی وجود دارن که مانع از به وجود اومدن مجموعههایی مثل مجموعهی R میشن.
در تعریف مجموعهها در ZFC ، اصلی به نام اصل Foundation یا Regularity وجود داره که ریاضیات آن به صورت زیره:
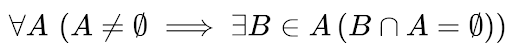
این به این معناست که برای هر مجموعهی A که تهی نباشه، حداقل یک عضو B وجود داره که هیچ عضوی از A ندارد (یعنی ∅ = B∩A). این اصل بهطور ساده بیان میکنه که هیچ مجموعهای نمیتونه به خودش عضو باشه. به عبارت دیگر، هیچ مجموعهای نمیتونه خودش رو شامل بشه (یا شامل مجموعهای بشه که خودش رو شامل میشه). این اصل، مجموعههایی مانند R را غیرممکن میکنه.
حالا به نظرت در تعریف عادی مجموعهها، تناقضهای دیگهای جز راسل وجود داشته؟ اگه آره، تا حالا تونستن همهشون رو حل کنن؟ یه سرچی در این مورد بکن!
در نهایت خوبه که اشاره کنیم به جملهی معروف گودل که میگه:
«گزارههایی در جهان وجود دارند که حقیقت دارند، اما با هیچ قانون و فرضهای اولیهای نمیشود اثباتشان کرد!»
رستایی باشی!