🎲 کارگاه «آمار و احتمال» یکی از ۴ کارگاهی بود که برای رویداد رستا در شهرستان بافق، برای دانشآموزان متوسطۀ دوم، طراحی و ارائه شد. توی این نوشته میخوایم با ۳ مسئله، از بین مسائلی که توی این کارگاه ارائه شد، کمی آشنا بشیم. اگه مسائل رو دوست داشتید، در انتهای هر بخش منابعی برای یادگیری بیشتر قرار گرفته که احتمالا مفید باشه براتون.
همچنین، هرجا سوالی داشتید و میخواستید با هم صحبت کنیم، کافیه بهمون پیام بدید:

این مسئله یکی از مسائل معروف احتماله که احتمالاً کلی باید کلنجار برید که خوب درکش کنید.
داستان از این قراره که یک مسابقۀ تلویزیونی برگزار شده که توش شرکتکننده باید از بین سهتا در یکیش رو انتخاب بکنه؛ پشت یکی از درها یک ماشین گرونقیمته و پشت دوتای دیگه بز! (بله، ما هم نمیدونیم چرا بز؛ ولی جدیجدی برگزار شده یه چنین مسابقهای)
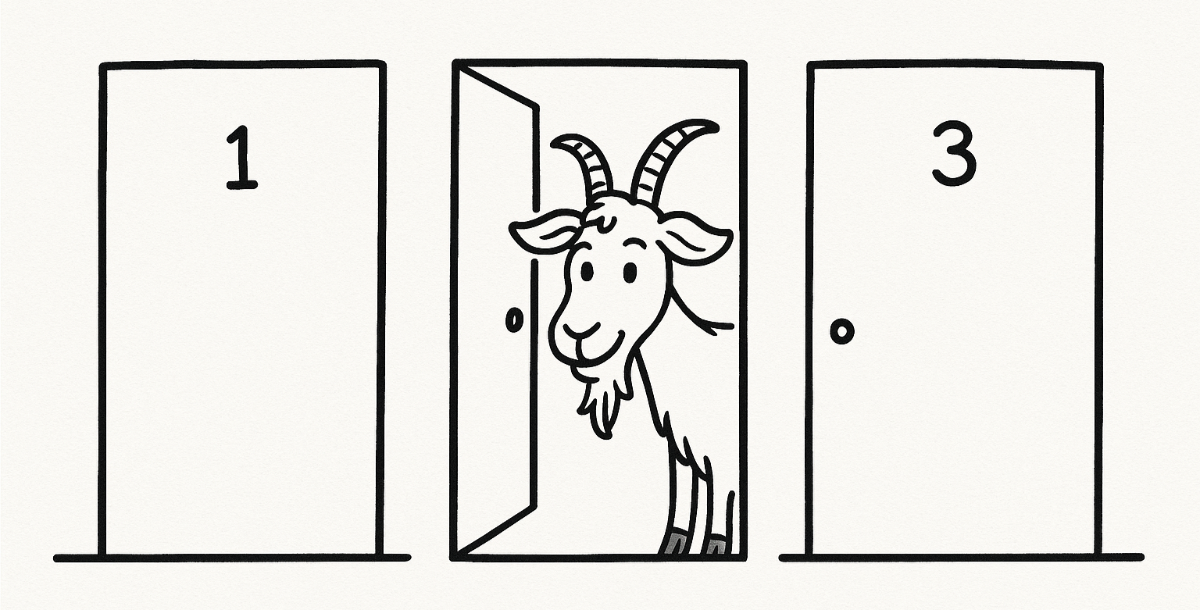
بعد از اینکه شرکتکننده یکی از درها رو انتخاب کرد، مجری قبل اینکه در انتخابشده رو باز کنه، از بین درهایی که انتخاب نکرده یکی که میدونه توش بزه رو باز میکنه و یه انتخاب پیش پای شرکتکننده میذاره:
«آیا میخوای انتخابت رو عوض کنی یا همونی که اول انتخاب کردی رو باز کنم؟»
به نظر شما تصمیم درست چیه؟ چرا؟
توی این سایت میتونید خودتون بازی کنید:
✅ جواب درست اینه که بهتره عوض کنید چون اگه عوض کنید احتمال برندهشدنتون ۲برابر میشه! آیا میتونید توضیح بدید که چرا؟ با شهودتون آیا ناسازگاره؟
🤔 شاید با خودتون میگید: «اول که انتخاب میکنیم، احتمال انتخاب درست یکسومه. بعد که یکی از درهای پوچ باز میشه، دوتا در میمونه که توی یکیش بزه و توی یکیش ماشین؛ بنابراین حالا احتمال یکدوم میشه چه عوض بکنیم و چه نکنیم»
اما این استدلال درستی نیست. میتونید برامون توضیح بدید چرا؟ (بهمون توی رستا اینفو بگید!)
حالا یک مسئلۀ مرتبط دیگه: ۳ کارت با ۳ رنگ متفاوت داریم: قرمز و سبز و آبی. کارتها رو بُر میزنیم و بعد روی میز بهپشت قرار میدیم. احتمال اینکه بهصورت تصادفی بتونیم کارت قرمز رو انتخاب کنیم، قاعدتاً یکسومه. (مگه نه؟) حالا فرض کنید یکی از کارتها رو من برمیدارم و بدون اینکه بگم چه رنگی بوده توی جیبم میذارم و ۲ تا کارت باقی میمونه. حالا اگه یکی از این ۲ تا کارت رو به صورت تصادفی بردارید احتمال اینکه قرمز باشه چقدره؟ [منبع: کتاب دو خطا در عنوان این کتاب وجود دارد. صفحه ۶۸]
خود صفحۀ ویکیپدیای این مسئله اطلاعات مفصل و توضیحات مفیدی داره.
چالش جالب میتونه این باشه که تلاش کنید این مسئله رو با شبیهسازی کامپیوتری حل کنید؛ یا با اکسل و گوگلشیت (مثلا با کمک این یا این راهنما) یا مثلاً با پایتون.
این مسئله یکی از مسائلیه که در کتاب فوقالعاده خواندنیِ دو خطا در عنوان این کتاب وجود دارد هم مطرح و توضیح داده شده ــــــ در کنار دهها مسئلۀ جذاب ریاضیاتی یا فلسفی دیگه ــــــ که شدیداً توصیه میکنیم مطالعه کنید.
به این سهتا سوال فکر کنید:
۱. آدمی رو در نظر بگیرید که عینکیه، به موسیقی کلاسیک علاقهمنده و همچنین اهل مطالعهست؛ احتمال اینکه این آدم یک استاد ادبیات باشه بیشتره یا فروشندۀ مغازه؟
۲. فرض کنید شما پزشک هستید و کسی به شما مراجعه کرده که سردرد شدید داره. صرفاً اگه با همین اطلاعات بخواید قضاوت کنید، احتمال اینکه دچار تومور مغزی باشه چقدره؟
۳. فرض کنید تست تشخیص سرطان ریه داریم که ۹۹٪ دقت داره: یعنی اگه سرطان داشته باشید، به احتمال ۹۹٪ میگه سرطان دارید و اگه نداشته باشید به احتمال ۹۹٪ میگه ندارید. حالا فرض کنید شما تست دادید و جواب تست مثبت بوده؛ چقدر احتمال داره که واقعاً سرطان داشته باشید؟
کمی فکر کنید و بهش جواب بدید، بعد ادامۀ متن رو بخونید :)
بیاید مسئلۀ سوم رو با هم حل کنیم:
برای حل این مسئله اطلاعات دادهشده کافی نیست! چیزی که نیاز داریم بدونیم اینه که سرطان ریه چقدر رایجه (یا به اصطلاح «نرخ پایه»اش چقدره). مثلا فرض کنید از هر ۱۰۰۰ نفری که برای تست سرطان ریه مراجعه میکنن، به طور میانگین ۱ نفر واقعاً سرطان داره، یعنی ۰٫۰۱ درصد. حالا، فرض کنید ۱۰۰هزار نفر این تستی که ۹۹٪ دقت داره رو دادهان؛ ما انتظار داریم به طور میانگین چنین نتیجهای بگیریم:
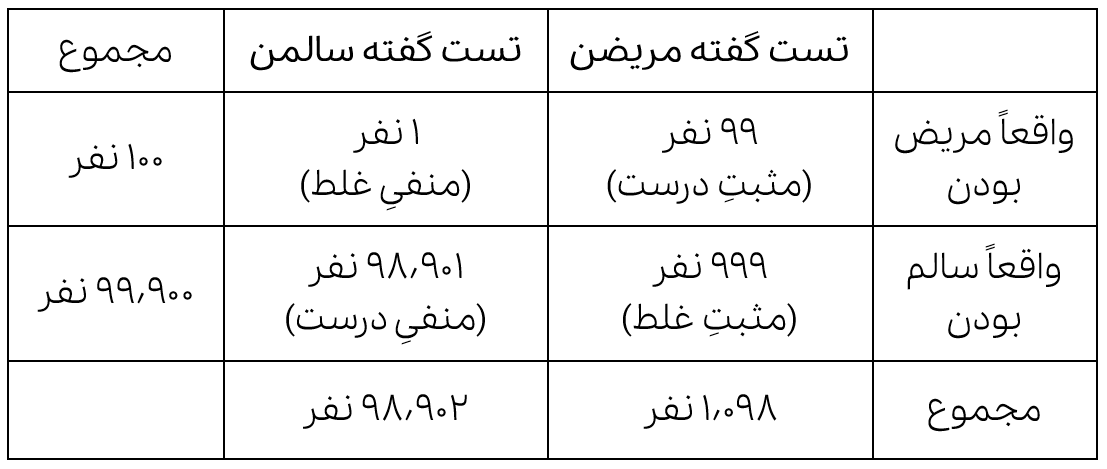
بنابراین، اگه تست کسی مثبت شد، احتمال اینکه واقعاً مریض باشه چقدر میشه؟ - فقط ۹٪ !
به بیان ریاضی:

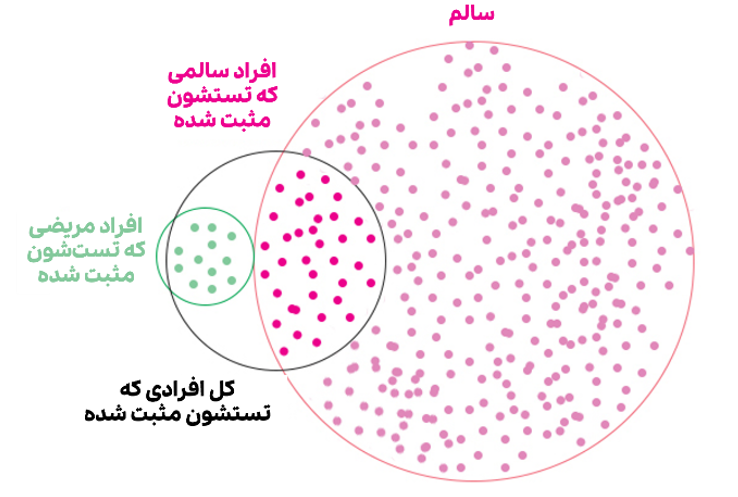
حالا، با چیزی که اینجا یاد گرفتید، پاسختون به سوالهای ۱ و ۲ چیه؟ بهمون بگید.
این مسئله در اصل مثالی از قضیۀ معروف بیزه (Bayes Theorem) که کلی منابع مختلف توضیحش دادهان و با کمی جستجو (یا صحبت با ChatGPT) میتونید یادش بگیرید و مسئلههای دیگهای ازش ببینید.
توی مسئلهای که دیدیم، دقت رو یکپارچه دیدیم و ۹۹٪ در نظر گرفتیم. اما چنین تستهایی در واقعیت دو مؤلفۀ متفاوت دارن: الف)Sensitivity یا حساسیت: یعنی دقت یک آزمایش در تشخیص بیماران واقعی از بین کل بیماران؛ و ب) Specificity یا تشخیص: یعنی دقت یک آزمایش در تشخیص افراد سالم واقعی از بین کل سالمها. توی این سایت میتونید این مقادیر رو تنظیم کنید و نتیجه رو ببینید.
همچنین توی این سایت هم میتونید یه شبیه سازی دیگه از این مسئله رو ببینید و لذت ببرید.
توی فصل ۲۸ کتاب هنر شفاف اندیشیدن، نوشتۀ رولف دوبلی، به این مسئله پرداخته میشه. این کتاب هم بسیار شیرین و خواندنیه و توصیه میکنیم مطالعه کنید.
تا حالا شده بخواید یه ادعایی رو محک بزنید ولی ندونید چطوری؟
مثلا این ادعا یکی بگه فرق نوشابۀ پپسی با کوکاکولا رو از طعمش تشخیص بده یا مثلاً فرق لباس نخپنبه یا پلیاستر رو با نگاه بفهمه.
با طراحی یک آزمایش آماری ما میتونیم چنین ادعاهایی رو محک بزنیم. چطور؟
همون ادعای تشخیص نوشابه رو در نظر بگیرید: یکی ادعا میکنه که میتونه بهدرستی از بین لیوانهای ظاهراً یکسان، با مزهکردن هر کدوم تشخیص بده که کدوم نوشابه پپسیه و کدوم کوکاکولا.
ما برای سنجش این ادعا یک تست طراحی میکنیم: ۱۲ تا نوشابه که ۶ تاش پپسیه و ۶ تاش کوکاکولا رو در ۱۲ لیوان یکسان میریزیم و اون فرد باید با مزهکردن اینها، ۶ تاش که بهنظرش پپسیان رو جدا کنه.

ما با این ادعا بدبینانه برخورد میکنیم، یعنی چی؟ یعنی ما فرض میکنیم که این آدم هم مثل بقیۀ آدمهاییه که نمیتونن تشخیص بدن و بنابراین حدسهاش شانسیه. (به این فرض، به زبان آماری، میگیم فرض صفر یا Null Hypothesis که میخوایم با کمک تست ردش کنیم) در چه صورتی ادعای این آدم رو مبنی بر اینکه یک توانایی ویژه در تشخیص داره میپذیریم؟ در صورتی که نتیجهای ببینیم که اگه فرض صفر ما درست بود، خییییلی بعید بود اون نتیجه رو ببینیم و به این ترتیب فرض صفرمون رد میشه. اما این میزان «بعید» بودن رو چطور میتونیم اندازهگیری کنیم؟
آیا اگه ۴ تاش رو درست حدس بزنه بعیده یا میتونسته شانسی باشه؟ ۵تا چطور؟ ۶تا چطور؟
حالا بیاید، با تکیه بر مقدمات احتمال و ترکیبیات، احتمال مشاهدۀ نتایج مختلف رو حساب کنیم. اولاً، در کل به چند شیوۀ مختلف میشه ۶ لیوان رو از بین ۱۲ لیوان متمایز انتخاب کرد؟
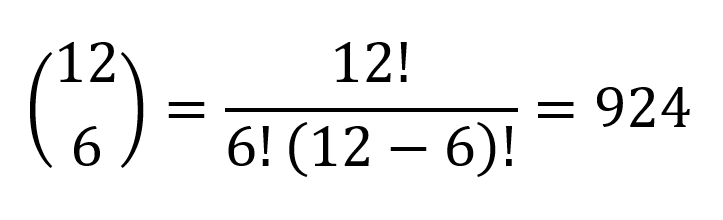
بنابراین در مجموع ۹۲۴ حالت داریم.
فردی که داریم آزمونش میکنیم، باید ۶ تا لیوان که نوشابه پپسی داره رو انتخاب کنه، که میتونه همش درست باشه، یا هیچکدوم، یا یه چیزی در این بین. بیاید احتمال رو برای هر کدوم محاسبه کنیم. (قبل از اینکه محاسبه کنیم، به نظرتون محتملترین نتیجه کدومه؟)
مثلاً، در چندتا از اون ۹۲۴ حالت انتخاب ۶ لیوان، ۲ تاش درست بوده؟
این یعنی تعداد حالتهای انتخاب ۲تا از بین ۶تا پپسی و انتخاب ۴تای مابقی از بین ۶ تا کوکاکولا که، با استفاده از قانون ضرب، به این صورت محاسبه میشه:
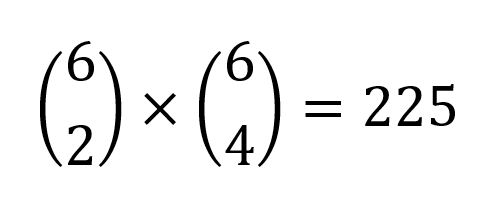
در نهایت اگه همۀ اینها رو حساب کنیم، چنین جدولی رو میتونیم بسازیم:
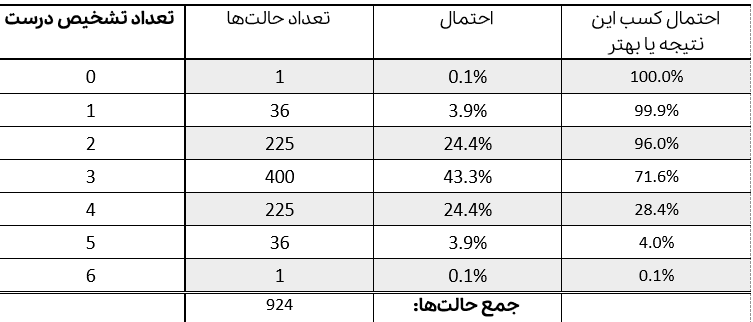
(توجه داشته باشید که این احتمال مشاهدۀ اون نتیجست، به شرط اینکه کاملاً تصادفی انتخاب شده باشه.)
حالا، همونطور که در جدول میبینید، یه ستون هم اضافه کردیم که در واقع جمع احتمال گرفتن اون نتیجه یا نتایج بهتر از اونه. بنابراین، اگه فرد شانسی انتخاب کرده باشه. مثلاً ۲۸٪ احتمال داره که ۴ تا یا بیشتر رو درست گفته باشه.
حالا، ما برای قضاوت باید اون «میزان بعید بودن» ای رو تعیین کنیم که اگه از اون حد بگذره ما متقاعد میشیم که اون تشخیصه شانسی نبوده. معمولاً در آزمونهای فرض، این مقدار، که بهش خطای آلفا میگن، رو ۱۰، ۵ یا ۱ درصد در نظر میگیرن. مثلاً اگه ملاک ما ۵٪ باشه، یعنی تا محدودۀ ۹۵٪ ما همچنان نمیتونیم بپذیریم که فرض صفر رد شده، ولی اگه از ۹۵٪ رد بشه، دیگه اونقدر بعیده که میگیم فرض صفر رد شده.
حالا توی مسئلۀ ما این ناحیه (که بهش میگیم «ناحیۀ بحرانی») میشه حالتهایی که ۵ یا ۶ تشخیص مشاهده بشه:
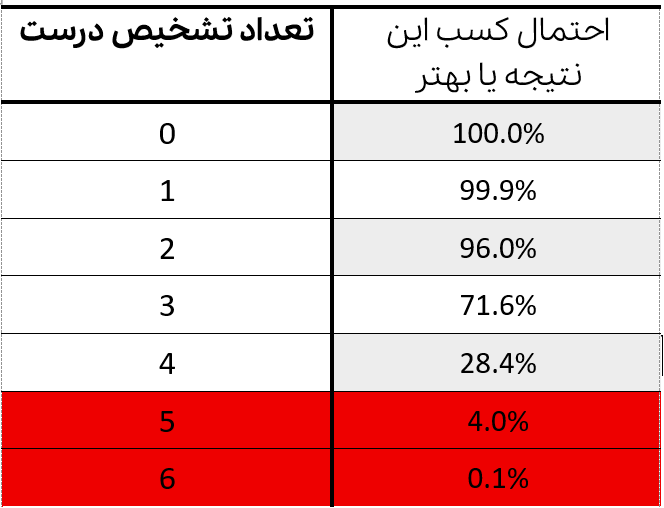
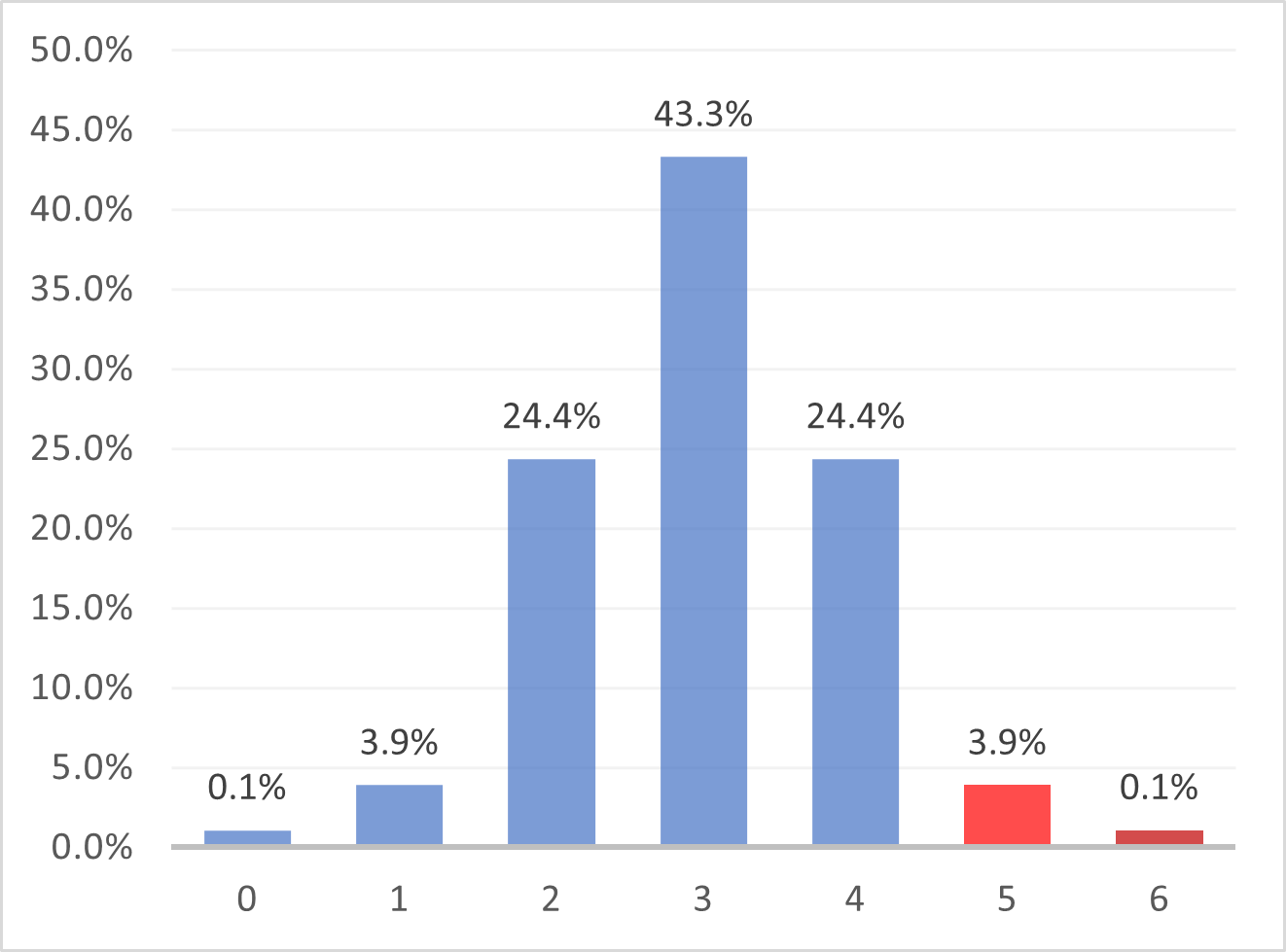
بنابراین، اگه آزمونشونده بتونه ۵ یا ۶ تاش رو درست تشخیص بده، ما میتونیم ادعاش رو بپذیریم که به احتمال قوی شانسی نبوده و واقعاً توانایی تشخیص داشته. خلاصه، با این آزمون میتونیم اون ادعا رو محک بزنیم. به طور کلی به این روندی که طی شد «آزمون فرض» میگن که یکی از مباحث مهم و جذاب در آماره و کلی جزئیات و ظرافت داره.
این مسئله در واقع نمونهاز «آزمون دقیق فیشر» بود. داستان معروفی هست از این قرار که رانلد فیشر، آماردان انگلیسی مشهور، روزی به خانمی برخورد که ادعا داشت میتونه تشخیص بده که در ترکیب چای و شیر ـــ که در انگلستان رایجه ـــ اول شیر داخل استکان ریخته شده یا چای. و آزمونی که فیشر برای این ادعا ترتیب داد همین بود که از او خواست که از بین ۸ استکان یکسان که ۴تاش به نوع اول آماده شده و ۴تاش به نوع دوم، تشخیص بده که کدوم ۴تا متمایزن. و این خانم به طرز جالبی هر ۴تا رو درست تشخیص میده. (که اگر شانسی انتخاب کرده بود، فقط یکهفتم احتمال داشت که بتونه هر ۴تا رو درست تشخیص بده) این داستان رو از اینجا میتونید بخونید.
برای یک چالش، ببینید که برای حالتی که فرد باید از بین ۲۰ تا استکان ۵ تاش که پپسیان رو تشخیص بده چطور میتونید محاسباتش رو انجام بدید و ناحیۀ بحرانی رو تعیین کنید.
دربارۀ آزمونهای آماری میتونید این صفحۀ دانشنامۀ ویکیپدیا رو مطالعه کنید.
دیگه چه مسئلهای در اطرافتون میبینید که حدس میزنید بشه براش یه آزمون آماری طراحی کرد؟
اینها بعضی از مسائلی بودن که در کارگاه «آمار و احتمال» امسال، در رویداد علمی رستا در شهرستان بافق ارائه شدن ــــــ هرچند با شکلی متفاوت از آنچه اینجا دیدید. البته مباحث این کارگاه به این مسائل محدود نبود و به مسئلههای دیگهای هم مثل پارادوکس سیمپسون، خطاهای نمونهگیری، سوگیری بازماندگی، همبستگی و علیت و تست دوجملهای پرداخته شد.
امیدواریم از خوندن این مطلب لذّت و فایدهای برده باشید.
خوشحال میشیم که مثل همیشه نظراتتون رو در رستا اینفو بشنویم و با هم در مورد این مسئلهها گفتگو کنیم.
به امید دیدار 👋