بازی زندگی

موضوعی که می‌خواهیم در مورد آن صحبت کنیم game of life یا Conway’s game of life و یا به اختصار life خوانده می‌شود. بازی زندگی یک اتوماسیون سلولی یا فضای سلولی است که توسط ریاضیدان بریتانیایی جان هورتون کانوی در سال 1970 ابداع شد.

خب برای درک بهتر بازی زندگی بهتر است ابتدا یک توضیح مختصر در مورد اتوماسیون سلولی بگوییم.

اتوماسیون سلولی یک مدل ریاضی است که سعی می‌کند چگونگی تغییر و تکامل سیستم‌های پیچیده را بر اساس قوانین ساده شبیه‌سازی کند.
این مدل از یک شبکه و آن شبکه از سلول‌های کوچک تشکیل شده که هر سلول می‌تواند وضعیت خاصی و محدود یا متناهی هم می‌توان گفت، داشته باشه مثل (مثل روشن/خاموش یا زنده/مرده یا صفر/یک). وضعیت هر سلول در هر لحظه به وضعیت خودش و همسایه‌هایش در لحظه قبل بستگی دارد.

بنابراین قوانین را به دوقسمت تقسیم میشود: 1.وضعیت فعلی سلول 2.وضعیت همسایگان

این ایده از کجا شروع شد؟

ایده اتوماسیون سلولی توسط استانیسواف اولام (Stanislaw Ulam) و جان فون نویمان در دهه 1940 مطرح شد. آن‌ها تلاش می‌کردند که متوجه این شوند چطور یک سیستم ساده می‌تواند خودتکثیری (Self-Replication) داشته باشد، درست مثل سلول‌های زنده

که بعدها در سال 1970 جان کانوی بازی زندگی را معرفی کرد که یکی از معروفترین مثال‌های فضای سلولی است.

بنابراین میتوانیم بگوییم که فضای سلولی یک بازی با قوانین ساده است که در آن هر سلول در یک شبکه، با توجه به وضعیت خودش و همسایه‌هایش تصمیم می‌گیرد "چطور تغییر کند". این بازی نشان می‌دهد که قوانین ساده می‌توانند رفتارهای پیچیده و الگوهای شگفت‌انگیز ایجاد کنند.

اتوماسیون سلولی را می‌توان در هر تعداد بعد اجرا کرد، اما رایج‌ترین انواع آن عبارتند از:

یک بعدی: سلول‌ها در یک خط مستقیم قرار دارند.

هر سلول فقط با همسایه‌های چپ و راست خود تعامل دارد.

دوبعدی: سلول‌ها در یک شبکه مربعی قرار دارند.

هر سلول با 4 یا 8 سلول اطراف خود تعامل دارد .

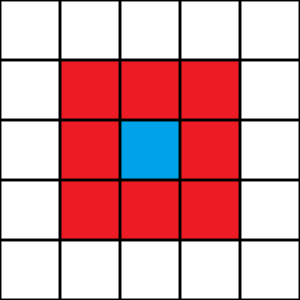
که این تعداد سلول ها به دو قانون همسایگی برمیگردد. قانون فون نویمان می‌گوید که سلول‌ها فقط با سلول‌های متعامد خودشان در ارتباط هستند. قانون مور می‌گوید علاوه بر سلول‌های متعامد با سلول‌های قطری نیز در ارتباط هستند که 8 همسایه می‌شود.

بازی زندگی نمونه‌ای از اتوماسیون سلولی دوبعدی است.

سه بعدی: سلول‌ها در یک شبکه سه‌بعدی (مثل مکعب) قرار دارند. مثل مدل‌سازی رشد تومورها یا گسترش بیماری‌ها.

ابعاد بالاتر نیز عمدتاً در ریاضیات نظری و فیزیک استفاده می‌شوند.

حال که در مورد تاریخچه این موضوع فهمیدیم به خود بازی زندگی می‌پردازیم.

بازی زندگی هم یک مدل ریاضی ساده است که روی یک شبکه دوبعدی از سلول‌ها اجرا می‌شود. هر سلول می‌تواند یکی از دو حالت زیر را داشته باشد:

زنده (1)

مرده (0)

زمان در این بازی به صورت گسسته پیش می‌رود، و وضعیت هر سلول در هر مرحله (نسل) بر اساس قوانین مشخصی تغییر می‌کند.

قوانین این بازی مسلما بر اساس فضای سلولی پیش می‌رود یعنی به خود سلول و همسایه‌هایش بستگی دارد؛ بنابراین برای اینکه بتوانیم این بازی را طرح کنیم باید قوانین در یک چهارچوب انتخاب کنیم پس قوانین به شرح زیر هستند:

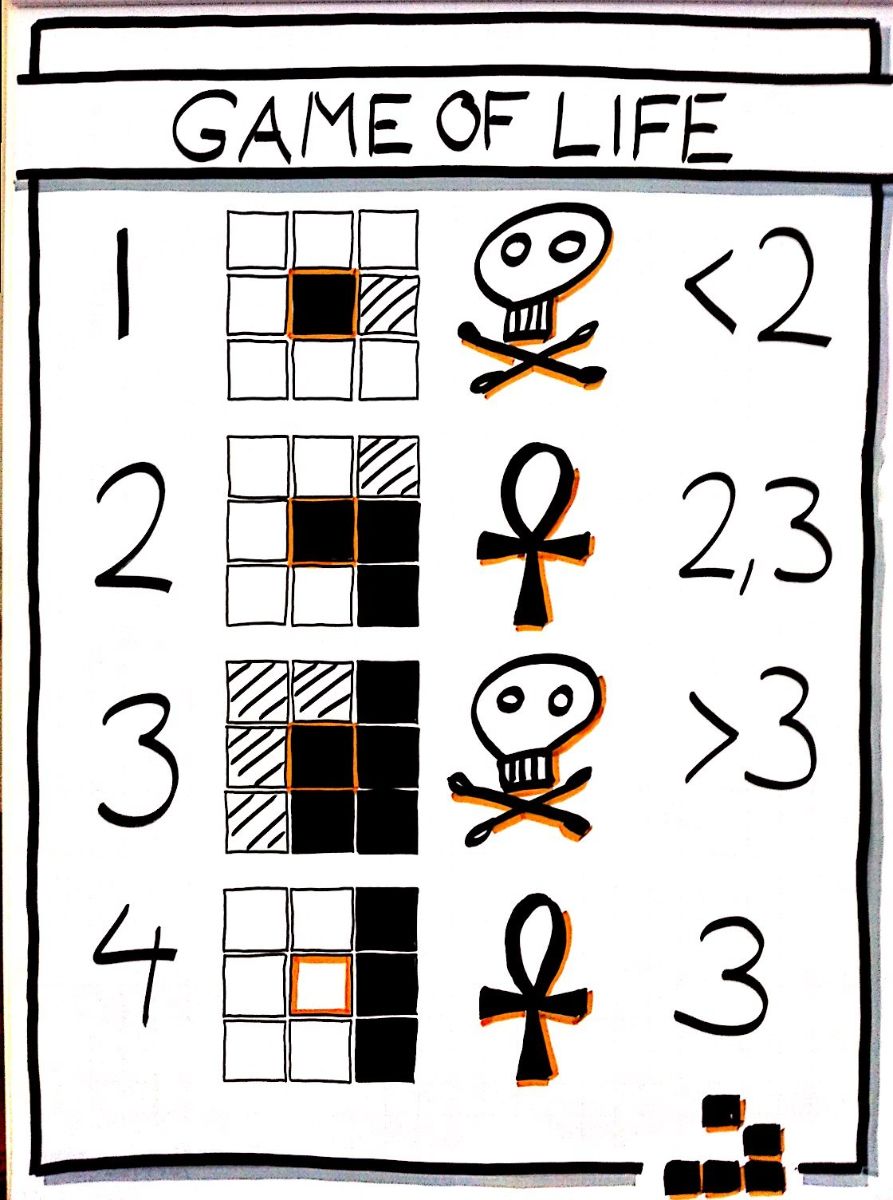
زنده ماندن:
اگر یک سلول زنده باشد و دقیقاً 2 یا 3 همسایه زنده داشته باشد، زنده می‌ماند.

مرگ به دلیل تنهایی:
اگر یک سلول زنده کمتر از 2 همسایه زنده داشته باشد، می‌میرد.

مرگ به دلیل تراکم زیاد:
اگر یک سلول زنده بیشتر از 3 همسایه زنده داشته باشد، می‌میرد.

تولد:
اگر یک سلول مرده دقیقاً 3 همسایه زنده داشته باشد، زنده می‌شود.

چگونه بازی شروع می‌شود؟

شبکه اولیه:
بازی با یک "پیکربندی اولیه" (Initial Configuration) شروع می‌شود، که شامل مشخص کردن سلول‌های زنده و مرده است. این پیکربندی معمولاً به صورت دستی یا تصادفی تنظیم می‌شود.

زمان و نسل‌ها:
با گذشت هر واحد زمانی (نسل)، وضعیت شبکه بر اساس قوانین بازی تغییر می‌کند.

بنابراین می‌توانیم بگوییم که الگوی آغازین بازی به عنوان بذر سیستم به حساب می‌آید. اولین نسل در بازی با اعمال قوانین فوق بر تک تک سلول‌ها به صورت همزمان ایجاد می‌شود و در آن زاد و ولدها و مرگ و میرها اتفاق می‌افتد. این رویه تا ایجاد نسل‌های آینده ادامه می‌یابد. بدین ترتیب هر نسل تابعی از نسل ما قبل خود خواهد بود.

با توجه به شرایط اولیه می‌توان گفت ما سه نوع متفاوت از بازی زندگی داریم:

stable patterns _ oscillators _ spaceships

علت تفاوت در بذر آنهاست که الگوهای ثابت به‌طور طبیعی به یک وضعیت پایدار می‌رسند، زیرا شرایط اولیه به گونه‌ای است که سلول‌ها نمی‌توانند تغییرات بیشتر ایجاد کنند.

نوسانگرها به دلیل تعاملات خاص بین سلول‌ها به یک حالت تکراری باز می‌گردند که در آن وضعیت‌های مختلف به‌طور متناوب تغییر می‌کنند.

فضاپیماها به‌خاطر طراحی خاص شرایط اولیه، حرکت می‌کنند و می‌توانند در طول زمان به مکان‌های جدید در شبکه منتقل شوند.

کاربردهای بازی زندگی:

بازی زندگی در ابتدا به‌عنوان یک سرگرمی معرفی شد، اما در طول زمان کاربردهای زیادی در زمینه‌های مختلف پیدا کرده است. برخی از این کاربردها عبارتند از:

مطالعات زیست‌محیطی:

در مسائل مربوط به محیط‌زیست و بوم‌شناسی، از مدل‌های مشابه بازی زندگی برای شبیه‌سازی فرآیندهای اکولوژیک و بررسی نحوه رشد و تعامل گونه‌ها در یک اکوسیستم استفاده می‌شود. بازی زندگی می‌تواند به تحلیل نحوه گسترش گونه‌ها و تأثیرات متقابل موجودات بر محیط کمک کند.

مدل‌سازی رفتار جمعی:

در علم فیزیک، بیولوژی، و اقتصاد، بازی زندگی می‌تواند برای شبیه‌سازی و مطالعه رفتار جمعی موجودات، مانند مغناطیس‌ها، سیستم‌های بیولوژیکی، یا رفتارهای اقتصادی استفاده شود. به‌ویژه در مطالعه پدیده‌های پویای جمعی مانند تغییرات در جمعیت‌ها، طوفان‌ها، و بحران‌ها می‌توان از بازی زندگی برای مدل‌سازی نحوه تعامل‌ها و پیش‌بینی نتایج استفاده کرد.

و مثال‌ها و کاربردهای دیگر ..

در آخر می‌توان گفت بازی زندگی یک مدل جذاب و ساده است که نشان می‌دهد چگونه قوانین ساده می‌توانند به الگوهای پیچیده و متنوعی منجر شوند