مرتبسازی حبابی یکی از سادهترین و کندترین الگوریتمهایی است که برای مرتبسازی استفاده میشود. این الگوریتم به گونهای طراحی شده است که بالاترین مقدار در یک لیست داده، در طول تکرارهای (Pass) الگوریتم مانند حباب به بالای لیست میآید. این الگوریتم به حافظه اجرایی کمی نیاز دارد، زیرا تمام مراحل مرتبسازی درون ساختار داده اصلی انجام میشود و نیازی به تعریف ساختار داده جدید به عنوان حافظه موقت نیست. همچنین این الگوریتم در دستهبندی In-Place (درجا) قرار میگیرد. الگوریتم مرتبسازی حبابی به دلیل آن که ترتیب نسبی عناصر با مقدار برابر را حفظ میکند در دستهبندی Stable (پایدار) نیز قرار میگیرد، همچنین از دیگر ویژگیهای این الگوریتم میتوان به Incremental بودن آن (یعنی دادگان به صورت تدریجی و مرحله به مرحله مرتب خواهند شد) و Adaptive بودن آن (یعنی اگر دادگان تقریبا مرتب باشند، سریعتر اجرا خواهد شد) نیز اشاره کرد.
بدترین عملکرد این الگوریتم O(N^2) است که به عنوان پیچیدگی زمانی درجه دوم شناخته میشود که در آن N تعداد عناصر است. توصیه میشود که این الگوریتم فقط برای مجموعهدادههای کوچک استفاده شود، البته محدودیتهای پیشنهادی برای تعداد عناصر (N) در استفاده از مرتبسازی حبابی به حافظه و منابع پردازشی موجود بستگی دارد، اما بهطور کلی بهتر است تعداد عناصر (N) کمتر از ۱۰۰۰ در نظر گرفته شود.
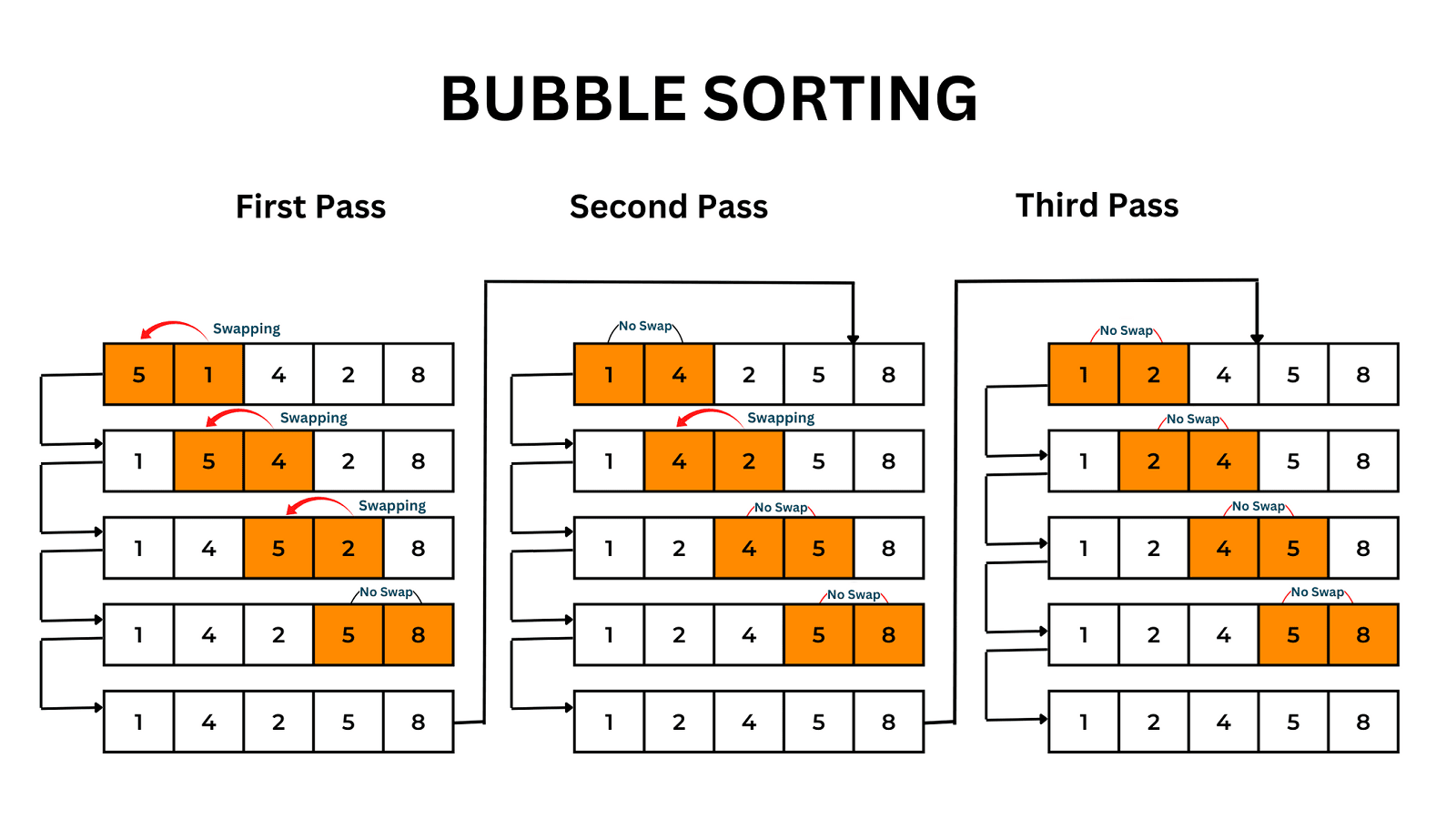
مرتبسازی حبابی بر اساس تکرارهای مختلفی کار میکند که به آنها Pass میگویند. برای یک لیست با اندازه N، مرتبسازی حبابی به N-1 عدد Pass نیاز دارد. به طور مثال، هدف Pass اول این است که بالاترین مقدار به بالاترین اندیس (بالای لیست/انتهای لیست) منتقل شود. به عبارت دیگر، در طول Pass اول، بالاترین مقدار لیست بهصورت یک حباب به بالای لیست حرکت میکند. منطق مرتبسازی حبابی بر اساس مقایسه مقادیر همسایه مجاور است به همین دلیل این الگوریتم در دستهبندی الگوریتمهای مرتبسازی مقایسهای (Comparison Sort) نیز قرار میگیرد. اگر مقدار در اندیس بالاتر از مقدار در اندیس پایینتر بیشتر باشد، مقادیر را جابجا میکنیم.
توجه کنید که بعد از Pass اول، بالاترین مقدار در بالای لیست قرار میگیرد و در اندیس آخر ذخیره خواهد شد. به همین ترتیب هدف Pass دوم این است که دومین مقدار بزرگ به دومین اندیس بالای لیست (اندیس یکی مانده به آخر) منتقل شود. برای این کار، الگوریتم دوباره مقادیر همسایه مجاور را مقایسه میکند و در صورت عدم ترتیب صحیح، آنها را جابجا میکند. Pass دوم مقدار موجود در بالاترین اندیس را که در Pass اول در جای صحیح قرار گرفته است را شامل نمیشود. بنابراین، یک عنصر داده کمتر برای پردازش وجود خواهد داشت.
نمونهای از پیادهسازی الگوریتم مرتبسازی حبابی در پایتون را میتوانید در gist زیر مشاهده کنید.
پیادهسازی قبلی از مرتبسازی حبابی که با تابع bubble_sort انجام شده است، یک پیادهسازی ساده از این الگوریتم است که در آن عناصر مجاور بهطور مکرر مقایسه و در صورت عدم ترتیب صحیح جابجا میشوند. این الگوریتم در بدترین حالت به O(N^2) مقایسه و جابجایی نیاز دارد، زیرا برای یک لیست با N عنصر، بدون توجه به ترتیب اولیه لیست، الگوریتم بهطور قطعی N-1 عدد Pass را اجرا میکند!
نمونهای از پیادهسازی الگوریتم مرتبسازی حبابی بهبود یافته در پایتون را میتوانید در gist زیر مشاهده کنید.
تابع optimized_bubble_sort بهبود قابل توجهی در عملکرد الگوریتم مرتبسازی حبابی ایجاد میکند. با اضافه از یک فلگ swapped، الگوریتم میتواند قبل از انجام تمام N-1 عدد Pass، تشخیص دهد که آیا لیست از قبل مرتب شده است یا خیر. وقتی یک Pass بدون هیچ جابجایی تمام میشود، این نشانه واضحی است که لیست هماکنون مرتب شده است و الگوریتم میتواند زودتر از موعد، پایان یابد. بنابراین، در حالی که بدترین پیچیدگی زمانی برای لیستهای کاملاً نامرتب یا معکوسمرتبشده O(N^2) باقی میماند، بهترین پیچیدگی زمانی برای لیستهای از قبل مرتبشده به O(N) بهبود مییابد.
خب به راحتی میتوانیم ببینیم که مرتبسازی حبابی شامل دو سطح حلقه است:
مطالب برگرفته از کتاب:
50 Algorithms Every Programmer Should Know: Tackle computer science challenges with classic to modern algorithms in machine learning, software design, data systems, and cryptography 2nd ed. Edition by Imran Ahmad (Author)