رمزنگاری کاربردی - قسمت هفتم : Signatures & zero-knowledge proofs

در فصل هفتم از کتاب اقای david wong به مبحث امضای دیجیتال و یه موضوع دیگه میپرداریم (Signatures and zero-knowledge proofs) ، طبق معمول توصیه میشه قسمت های قبل رو از این لینک بخونید و سری مقدماتی رو هم خونده باشید

مطالب پیوسته هست و اگر مطالب قبلی رو نخونده باشید توی درک مطالب جدید و ارتباط همه مطالب باهم به مشکل میخوریم

آقای وونگ خیلی ساده اشاره میکنه که امضای دیجیتال مثل امضای واقعیه، کلمه ایم ک براشون بکار میره digital signatures یا signature schemes هست

🔸7.1 What is a signature?

برای امضای دیجیتال ما نیاز به یک جفت کلید عمومی داریم، یه الگریم برای امضای دیجیتال (signing algorithm) که کلید خصوصی و پیام رو بگیره و امضا رو تحویل ما بده و یه الگریتم برای اعتبار سنجی و تایید صحت امضا (verifying algorithm) که کلید عمومیو با پیام و امضا میگیره و True یا Flase برمیگردونه

به کلید عمومی signing key هم گفته میشه و به کلید خصوصی verifying key هم میگن

با امضا میشه به چی رسید؟

هم میشه مطمئن شد که فرستنده نامه ، همونیه که ما منتظر پیام از سمتش بودیم (Origin) و هم میشه مطمئن شد که پیام توی حین ردوبدل شدن تغییری نکرده (Integrity)

شاید فک کنید ک امضای دیجیتال شباهتی به MAC که خوندیم داره و درست فکر میکنید، ولی تفاوتی که امضای دیجیتال با MAC داره اینه که ما میتونیم پیام هارو احراز هویت کنیم (بدون دونستن کلید خصوصی)

🔸7.1.1 How to sign and verify signatures in practice

در ادامه یه کد پایتون میبینیم که میاد خیلی ساده یه جفت کلید عمومی میسازه، و با کلید خصوصی پیامو امضا میکنه، و با کلید عمومی پیامو اعتبار سنجی میکنه

🔸7.1.2 A prime use case for signatures: Authenticated key exchanges

مشکلی که توی فصل 5 یا 6 داشتیم این بود که ما با وجود پروتوکل هایی برای تبادل کلید، هنوز دستخوش MITM میشدیم و نمیشد فهمید که فرد مقابل آیا اونی هست که ادعا میکنه یا نه

ما مفهوم authenticated key exchange رو داریم که ترکیب امضای دیجیتال و تبادل کلیده، و خیلی ساده هر فرد وقتی میخواد ارتباط بگیره ، (درصورتی که باب از قبل کلید عمومی آلیس رو داشته باشه) آلیس قصه ما میاد کلید میسازه و میخواد کلید عمومی که ساخته رو بده به باب، میاد و ازش با کلید خصوصی امضا میگیره و میفرسته

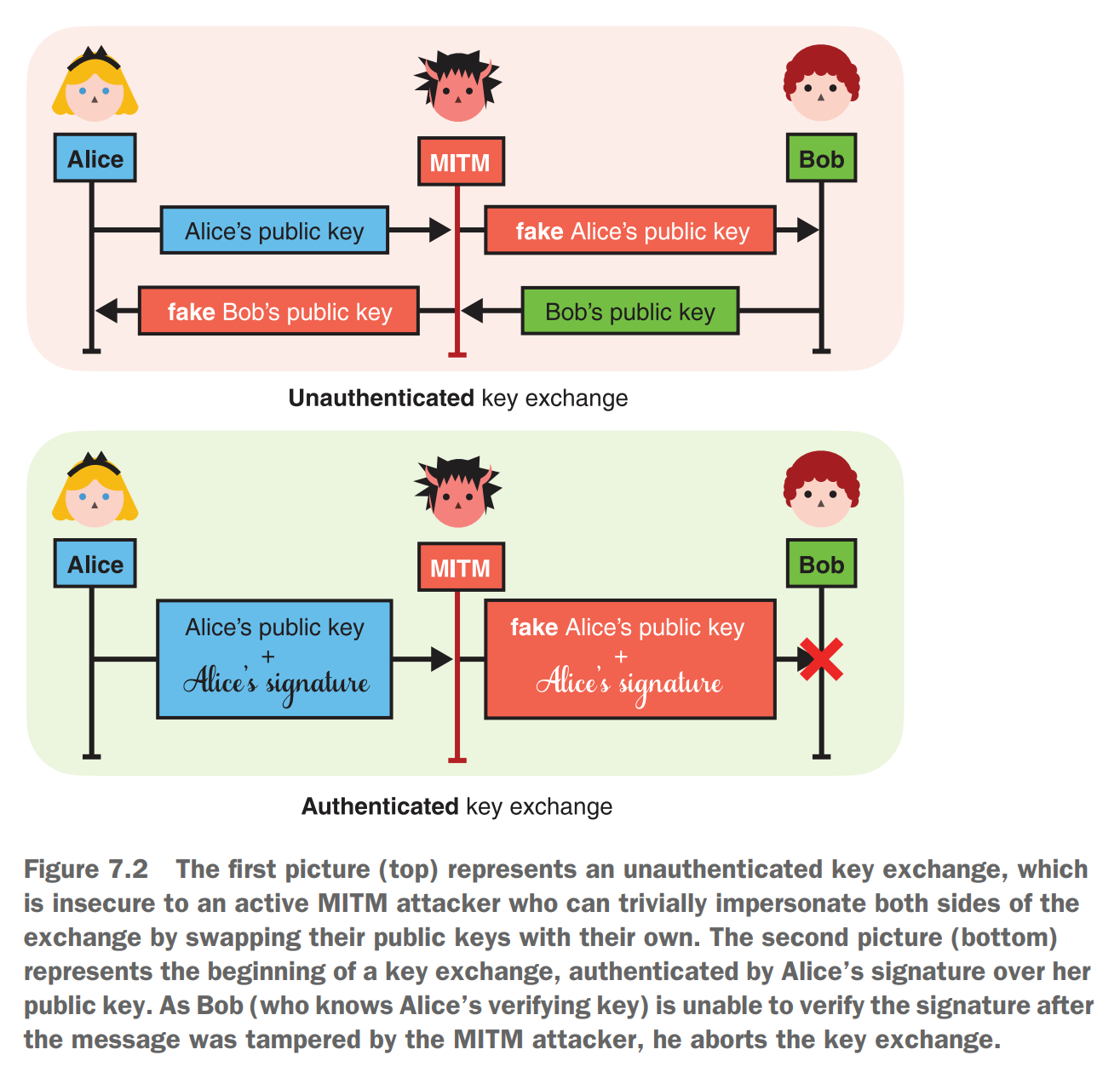
خب حالا نکته داستان بالا اینه ک باب کلید آلیس رو داره ولی آلیس کلید بابو نداره، اسم این انتقال کلید میشه authenticated key exchange ولی اگر هردو کلید عمومی همو از قبل داشته باشن اسم این انتقال کلید میشه mutually-authenticated key exchange

🔸7.1.3 A real-world usage: Public key infrastructures

بحث Transitivity of trust بحث جالبیه ، فرض کنید شما به من اعتماد دارید و من به فرد دیگری، پس شما در این جریان میتوانید به فرد دیگری (بخاطر اعتمادی که بینمون هست) اعتماد کنید

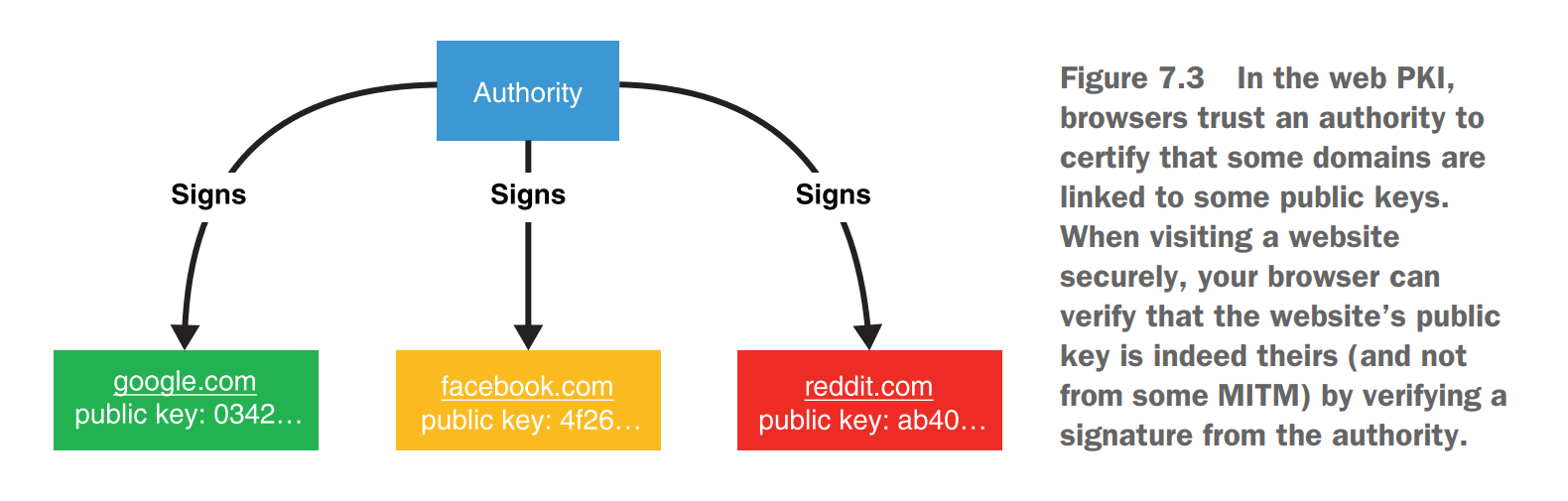
حالا فرض کنید ما یه authority یا یه مرجع داریم (یه شرکت مثل گوگل مثلا ) داریم یا یه مرجعی که همه بهش اعتماد دارن، اگر اون بیاد و کلید عمومی افرادی مثل bob یا charles یا ... رو امضا کنه ، شما اگر خواستید با اون فرد ارتباط بگیرید خیلی راحت میتونید کلید عمومیشو از اون authority یا مرجع چک کنید ، این مفهوم رو توی وب ما تحت عنوان web public key infrastructure (web PKI) داریم؛ از web PKI مرورگر ها استفاده میکنن، قبل اینکه شما از سایتی بازدید کنید، مرورگر با اون سایت key exchange انجام میده و با web PKI مرورگر از این تبادل کلید اطمینان حاصل میکنه (خلاصش شد وقتی شما از سایتی بازدید میکنید ، مرورگر تبادل کلید میکنه برای ساخت یه تونل امن، حالا واسه اینکه مطمئن بشه با فرد دستی داره تبادل کلید میکنه، از web PKI استفاده میکنه) ، توی شکل 7.3 این چیزی که توضیح دادیم هست

نکته فنی : وقتی یه مرورگری دانلود میکنید، سازنده توی کد اون مرورگر یه سری verifying key میزاره که اینا مربوطن به authority هایی که کلید عمومی هزاران هزار سایت رو امضا کردن و معروفن، پس شما خیلی راحت میتونید بهشون اطمینان کنید.

🔸7.2 Zero-knowledge proofs (ZKPs): The origin of signatures

قبل عمیق تر شدن توی بحث امضای دیجیتال باید این مفهومو باهم بررسی کنیم

آقای وونگ مثال جالبی نمیزنن سر همین خودم توضیح میدم ، فرض کنید شما یه چیزی میدونید و میخواید به یکی اثبات کنید که من این رو میدونم، ولی در عین حال نمیخواید اون اطلاعات رو افشا کنید، درسته؟ خب شما Prover حساب میشید و اون فردی که میخواید بهش اثبات کنید Verifier ، شما به هزاران روش میتونید به اون اثبات کنید که اون اطلاعات رو دارید و یا میدونید ، بدون اینکه اون هارو لو بدید !

مثلا شما جواب یه فرمول ریاضی رو میدونید و به دوستتون میگید من اینو میدونم، دوستتون میگه خب جوابش چیه؟ هردو باهم میرید پیش کسی که جوابو میدونه، شما توی گوش اون جوابو میگید و ازش میخواید اگر درست گفتید تایید کنه، و اون جلوی دوستتون این مورد رو تایید میکنه و دوستتون بدون اینکه جواب فرمول رو بفهمه ، مطمئن میشه که شما اون رو میدونید، یا مثلا شما به دوستتون میگید که میدونید تاریخ انتشار GTA جدید کی هست، دوستتون میگه بگو ببینم، شما این رو توی یه کاغذ مینویسی و میندازیش توی یه گاوصندوق امن(حالا فرض کنید هیچ کدوم دسترسی ندارید) و وقتی GTA جدید امد بیرون میرید و گاو صندوقو باز میکنید و دوستتون کاغذو میبینه و مطمئن میشه که شما اینو میدونستید

این مکانیزم همونطور که از اسمش پیداس، knowlede یا علم یا یه اطلاعاتی رو proof یا اثبات میکنه، ایده اینه که هیچ اطلاعاتی توی این اثبات افشا نشه، ریاضیشم اینه که شما یه اظهار یا ادعایی داری، مثلا شما جواب یه فرمول ریاضی ( مثلا f(x) ) رو میدونی، این ظهار یا Statement میشه S و اون جواب میشهx ،حالا ما میخوایم ثابت کنیم S درسته بدون اینکه x رو افشا کنیم

یه دسته از ZKP ها interactive ان ، یعنی واکنشی کار میکنن و نیاز دارن که فردی که مدعی هست با اون عا تعامل داشته باشه تا این صحت رو بسنجن ، یعنی چی؟ اگر شما یه سیستم رو Verifier در نظر بگیری و یه ادم که میخواد اعتبار سنجی کنه رو Prover ،سیستم میاد از اون فرد سوال میپرسه (اصطلاحا یه چالش یا Challenge ارسال میکنه برای طرف) و این ارسال چالش چندین بار صورت میگیره، طرف باید این چالش هارو حل کنه و بفرسته برای سیستم و سیستم از جواب درست میفهمه که این فرد اون راز یا اطلاعات رو میدونه

(مثلا فرض کنید شما یه رمز 20 رقمی میدونید، سیستم میاد چالش میده و میپرسه که 5 رقم اول چیه؟ شما میگی تاریخ حمله به برج های دوقولو (اینجا اشاره به عدد 09/11 نمیکنید اصلا) و اون میدونه که شما از رمز خبر داری وگر ن نمیدونستی 4 رقم اول رمز 0911 هست)

این چالش ها معمولا به تعداد دفعات اتفاق می افته که مطمئن بشن Prover چیزی رو حدس نمیزنه یا تلاش نمیکنه حمله ای بکنه که بر اساس زمان بندیه (توی فصل MAC خوندیم)

کاربرد های فراوانیم دارن، مثلا توی بحث Cryptocurrencies توی سیستم های حفظ حریم خصوصی در Zcash استفاده شدن و... خیلی کاربرد دارن امروزه

حالا جریان اسم گذاری اون Zero توی Zero Knowledege Proof چیه؟ ما گفتیم سیستمی میخوایم که Prover اطلاعاتی رو (Knowledege ) به Verifier اثبات کنه (Proof) ، اگر این اثبات بدون افشای اون اطلاعات باشه، یه کلمه Zero میاد اول اسم ، یعنی هیچ اطلاعاتی افشا نمیکنم(Zero Knowldege) ولی اثبات میکنم

همونجور که تا الان فهمیدید ، پروتوکل های ZKP دو دسته هستند، یک دسته Interactive و دومی Non Interactive ، میخوایم جفتشو بررسی کنیم:

🔸7.2.1 Schnorr identification protocol: An interactive zero-knowledge proof

میریم سراغ پروتوکل های ZKP از نوع interactive ، اینجا مدرس Schnorr protocol رو بررسی کرده، که یه Prover (بهش میگه peggy) میخواد ثابت کنه که میدونه رمز یا secret که x هست چیه ، بدون اینکه افشاش کنه ! و میخواد شروع کنه به ساخت یه ZKP و کم کم با بررسی مشکلات و راه حل ها بهمون ایده بده ک پروتوکل امن رو چطوری باید ساخت؛ اولین راهی که به ذهن هر کسی میرسه اینه که این x رو مخفی کنه با یه عدد رندومی (encrypt اش کنه) ولی مشکلی که هست اینه که شخص اثبات کننده میخواد اثبات کنه که x اون مقدار ماست و باید x رو اثبات کنه نه یه عدد رندومی که نمیدونه ، برای این کار میریم سراغ روش جبری ، یه عدد رندوم (k) رو میخوایم اضافه کنیم به x :

s = k +x

اینجا s اون عدد مخفی نهایی ماست ، k عدد رندوم و x مقدار secret

اینجا peggy قصه ما میخواد اثبات کنه به victor قصه ما که x رو میدونه ، پس میاد k و s رو میده به victor و میگه خودت حساب کن دیگه، ویکتور نباید جوابو همینطوری از peggy قبول کنه و بگه خب باشه الان من محاسبه میکنم و جوابت درسته ، چرا؟ چون ممکنه peggy یه s و k رندوم فرستاده باشه ! ویکوتور اینو میدونه که : Y =g^x یعنی x ما توان یه generator عه به نام g (حالا هرچی خواستید در نظرش بگیرید، مثلا x رو بگیرید 8 و g رو 2 )

حالا victor واسه تایید این قضیه میاد از این رابطه استفاده میکنه :

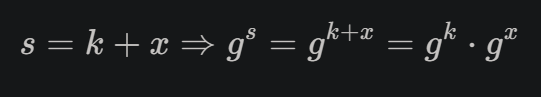
یعنی اگر peggy درست بگه ، پس من اگر این x رو بزارم توی فرمول باید درست در بیاد

(قبل ادامه بگم که وقتی میگیم 2 به توان 3 +4 ، یعنی 2 به توان 7 ، میتونیم جدا هم محاسبش کنیم ، یعنی یه بار 2 به توان 3 رو حساب کنیم، ضرب کنیم در 2 به توان 4 و جواب یکیه)

حالا peggy میگه خب s رو ک ب من داده اقای victor (برای مثال جلو من s رو 15 گرفتم ، k رو 7 و x رو 8 و g رو 2) و عدد 2 به توان s رو دارم ، k هم داده و به طبع 2 به توان k رو هم دارم ، از قبل خودم x رو هم دارم که 2 به توان x رو میخوام ضرب کنم در 2 به توان k و برسم به جواب :) پس victor میاد چک میکنه که ایا

این معادله بر قرار هست یا نه؟ (Y میشه g^x )

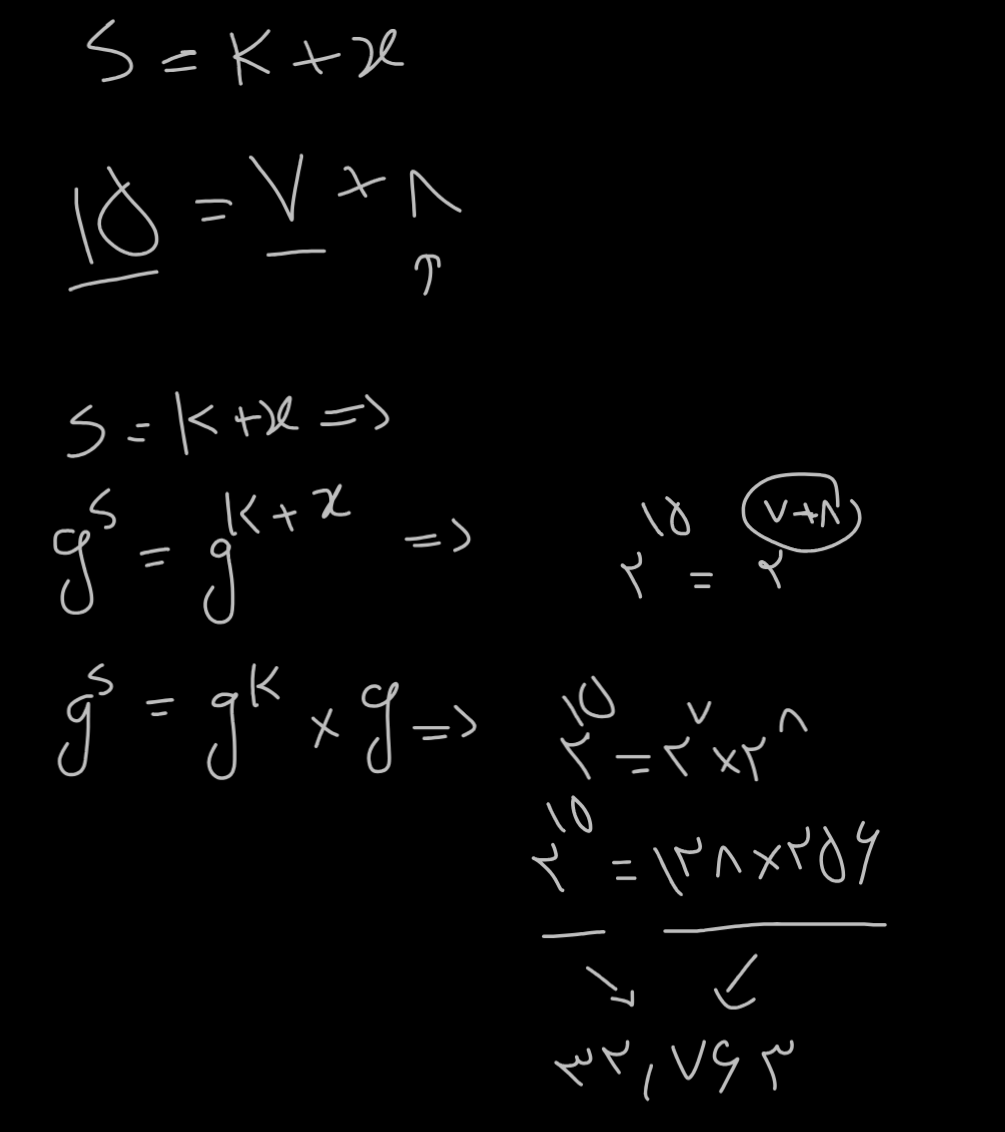
من توی عکس 125 این رو توضیح دادم، اعداد که معلومن ، اگر peggy درست بگه و x همون 8 باشه ، victor توی فرمول ها که جایگذاری کنه به جواب میرسه و معادله برقرار میشه (دو طرف مساوی میشه)

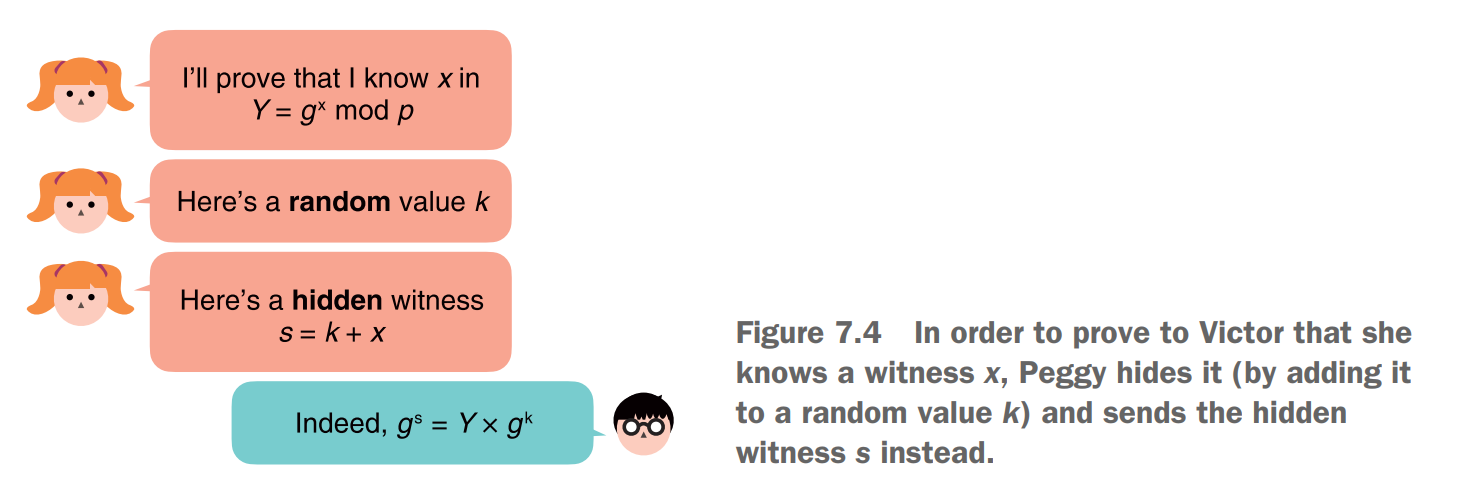
این فرایند یکم کنده ولی نه زیاد ، آمـــــــــا مشکلی که اینجا هست اینه که ما نمیخوایم victor یا همون verifier
ما بفهمه که x چیه !

کل قضیه همینه دیگه ! فقط peggy باید x رو بدونه و اون verifier باید اینو اعتبار سنجی کنه ، بدون اینکه بدونه چیه !!

الان victor بیاد بگه خب

x = s - k

میاد راحت x رو بدست میاره !

برای حل این ، کاری که peggy باید بکنه اینه ک k رو مستقیم نفرسته ، بیاد g به توان k یا g^k رو بفرسته

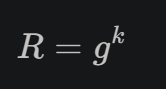
پس معادله این میشه :

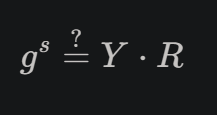
درواقع این :

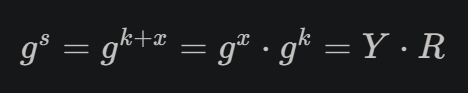
حالا دیگه victor هم نمیتونه به x دسترسی پیدا کنه ولی میتونه تاییدش کنه !

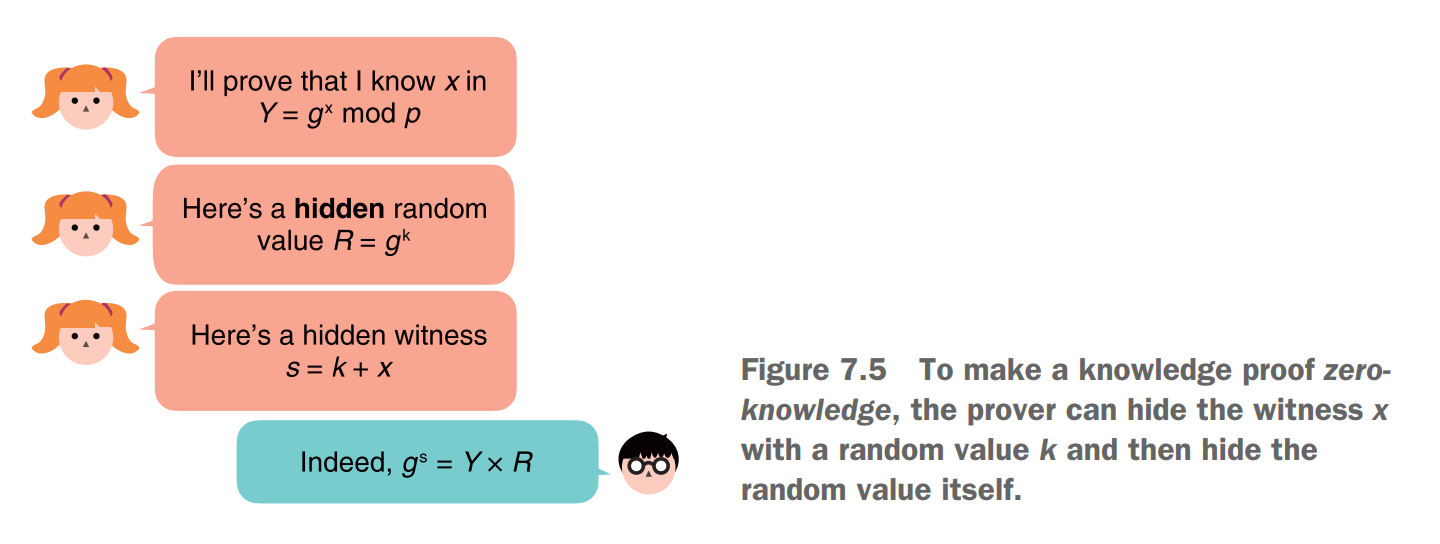
توی عکس بالا فرایندش توضیح داده شده

باز یه مشکل دیگه هست ، اینجا peggy میتونه تقلب کنه !! یعنی اگر ندونه x چیه میتونه جعلش کنه !

بزارید اول ریاضی شو توضیح بدم ، توی ریاضی ما جایگزینی داریم ، یعنی اگر مثلا بخوایم بگیم 2 + 3 = 5

میتونیم جای 2 بنویسیم 1+1 و معادله بشه این : (1+1) + 3 = 5

خط اول که فرمولیه که داشتیم ، توی خط دوم حمله رو توضیح دادم که peggy امده یه جایگزینی انجام داده ، جای g^x نوشته g^s × 1/g^k یعنی چی؟ امده Y رو برعکس کرده ، توی این عکس توضیحش میدم :

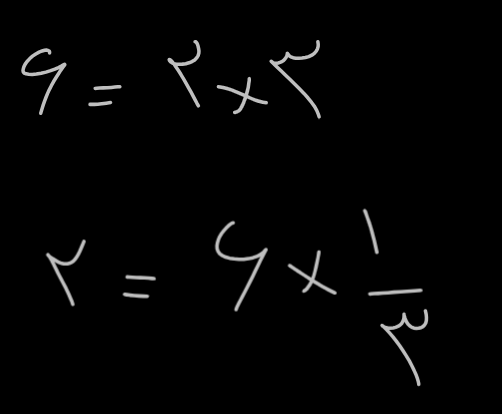
اگر ما 2 ضربدر 3 داشته باشیم ک بشه 6 ، در صورت نداشتن 2 میتونیم عدد دوم یا همون 3 رو برعکس کنیم و ضربدر عدد اصلی یا همون 6 کنیم

درواقع peggy امده Y^-1 رو زده که میشه معکوس Y و از جهتی که Y میشه g^k ، معکوس یا توان منفی در ریاضی میشه 1 تقسیم بر اون یا 1/g^k

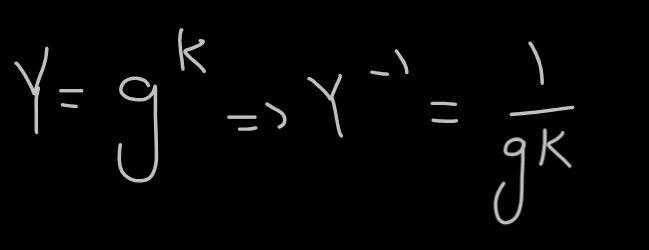
و همینو جای گذاری کرده ، یعنی امده یه عدد s تصادفی و رندوم انتخاب کرده و امده جعلش کرده

یعنی منطقی بگیم از طریق جبر و ریاضی امده g^x رو مهندسی معکوسش کرده که اون s رندومی که داده معتبر در بیاد

🔸نکته : این تکنیک که از معکوس استفاده کنی برای محاسبه یه مقدار توی خیلی از حملات استفاده میشه

🔸نکته : ما اصطلاح soundness رو در بحث ZKP داریم ، به این صورت که میگه یه متقلب که نمیدونه x چیه ، نباید بتونه verifier رو متقاعد کنه ، پس از لحاظ علمی و فنی ما میگیم پروتوکل ما sound نیست (protocol is not sound) چون peggy تونست تقلب کنه ! و اگر پروتوکل اجازه تقلب رو به کسی نده میگیم sound هست (the scheme is sound if Peggy cannot cheat)

حالا میخوایم پروتوکل رو sound کنیم ، میبریمش ب سمت ineractive بودن

اینجا victor باید مطمئن بشه که peggy نمیتونه s رو بعد دونستن Y محاسبه کنه :

1. اول peggy میاد عدد رندوم انتخاب میکنه برای k ، پس g^k ( یا همون R ) رو حساب میکنه و میفرستش به victor (اینجا در اصطلاح تخصصی میگن peggy متعهد میشه به عدد رندومش یا Peggy commits to her randomness ) و پس از این مرحله به هیچ عنوان دیگه نمیتونه k رو عوض کنه !

2. حالا victor یه چالش میفرسته به سمت peggy به اسم c (یه عدد رندوم انتخاب میکنه) ، این کار باعث میشه peggy نتونه تقلب کنه ، چون باید الان peggy بیاد و s رو با استفاده از اون چالش یا c محاسبه کنه ! یعنی در لحظه باید این کارو انجام بده و از قبل چیز اماده ای نداره ! (از قبل s رو ننشسته تولید کنه و محاسبات رو از روش ببره جلو)

3. حالا peggy میاد و s رو میسازه (الان اینجا اگر معتبر باشه حرفش باید x رو با c و x ترکیب کنه و به s برسه :

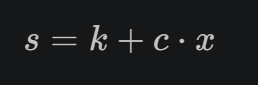
حالا victor میتونه فرمول رو چک کنه :

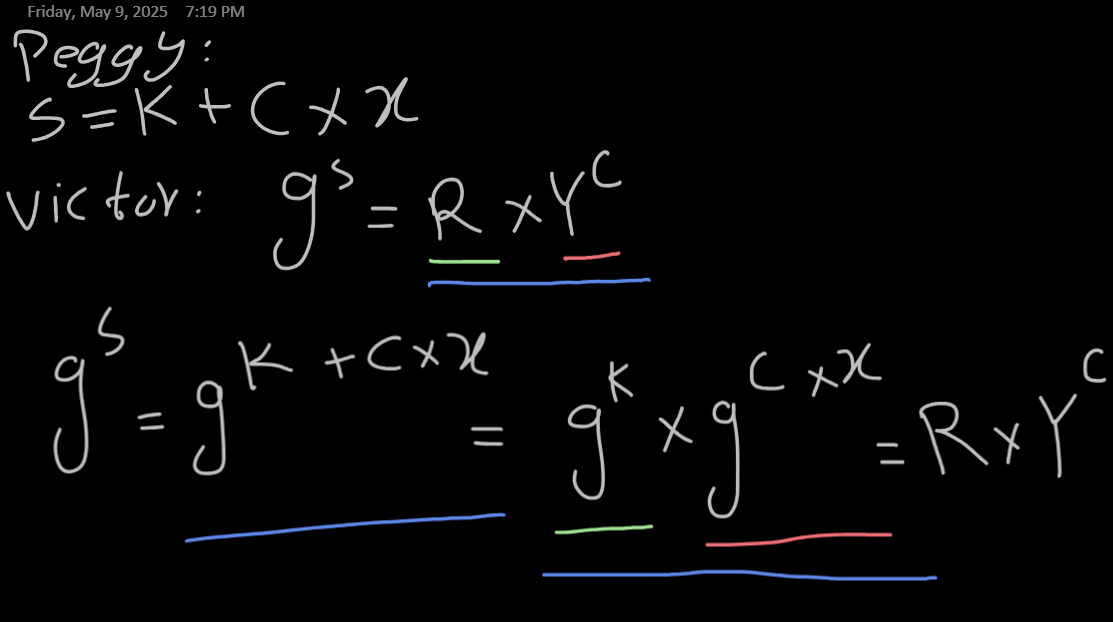
ویکتور میاد فرمول رو چک میکنه که مثل فرمول قبله ، فقط یه c اضافه شده که باید ضرب بشه در x در توان

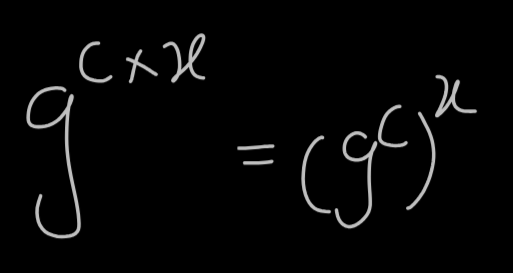
یعنی درواقع اول g به توان c میرسه ، نتیجه به توان x میرسه

حالا دیگه peggy نمیتونه تقلب کنه !

توی عکس 651 یه نکته ای هست ، توی فصل 2 که درباره hash صحبت میکردیم ، اگر خاطرتون باشه گفتیم که یکی از کاربرداش اینه که مثلا شما الان یه رمز و رازی داری ، میخوای به همه بگی که رمز رو داری ، ولی افشاش نکنی ، میایی اون رمز رو هش میکنی (مثلا : برنده جام جهان 2028 فرانسه است)و بعدا که جریان معلوم شد اینو رو کنی ، این هش الان ی جورایی مثل ZKP عمل میکنه (یجورایی!) و واقعا مثل اون نیست و خیلی محدودمون میکنه ،پس بجای هش ما از R = g^k استفاده میکنیم که k مخفی بمونه و از قابلیت توان بهره برده باشیم برای مخفی کاریمون :)

توی عکس 123 ما پروتوکل واقعی شناسایی schnorr رو داریم که هم کامله (یعنی peggy با صداقت victor رو متقاعد میکنه) ، هم sound عه (یعنی peggy نمیتونه تقلب کنه) و zero knowledge حساب میشه ( ویکتور هیچی از x نمیفهمه)

🔸نکته : به interactive ZKP system هایی که این سه تا ویژگی commitment - challenge - proof رو دارن میگن sigma protocols یا پروتوکول های سیگما و با حرف یونانی Σ نشونش میدن

🔸نکته : پروتوکولی که تا الان بررسی کردیم (schnorr) بر پایه صداقت verifier بنا شده ، بهش میگن (Honest Verifier ZK (HVZK))، یعنی امنیت پروتوکل Schnorr تا وقتیه که verifier یا victor قصه ما ادم خوبی باشه ، اگر بد باشه میتون challenge رو طوری بده ک x رو در بیاره (و عملا ZKP زیر سوال بره)

و تا همین حد بدونید که پروتوکل های ZKP های امنیم برای این منظور طراحی شده که جلوی این رو بگیره.

🔸7.2.2 Signatures as non-interactive zero-knowledge proofs

پروتوکل های interactive که ما گفتیم خیلی خوب و امنن، مشکلات خاص خودشونو دارن ، مثلا چی؟ اینکه دو طرف باید آنلاین باشن تا باهم ارتباط برقرار کنن (synchronous یعنی متقارن ، یعنی هردو باید هم زمان حضور داشته باشن) و اگر حتی یکی از طریقن بر خط نباشه امکان اعتبار سنجی نیست ! (asynchronous یعنی غیر همزمان ، مثل ایمیل که شما میزنید و طرفر بعدا میتونه جواب بده) و از طرف دیگه هم هزینه برن هم زمان بر (تعداد پیام های چالش و جواب باید ردو بدل شه و ساخت و اعتبار سنجی این پیاما زمان بره و اینکه انقد پیام باید ردوبدل شه هزینه بره) ، پس با اینکه پروتوکل های interactive خیلی خوبن ولی با استناد به دلایل بالا، توی دنیای واقعی زیاد استفاده نمیشن

دو نفر امدن یه راه حلی دادن که اسم راه حل اسم دوتاشون(Fiat-Shamir transform) و این راه حل اینطوری بود که میامد پروتوکل interactive رو میکرد non interactive ، حالا چطوری؟ اون فردی ک میخواد اثبات کنه یا prover ما میاد کل عناصر رو میزاره کنار هم و ازشون هش میگیره ، و چون میدونیم هش رندومه و غیر قابل پیش بینیه و غیر قابل کنترله و.. پس یه استرینگ خاصی در میاد (unique و یکتا میشه) و اون رو میفرسته به verifier (یکم جلوتر به شکل ساده تر توضیحش میدم)

پروتوکل (آقای) Schnorr که بررسی میکردیم آمد گفت اقا ما از این قابلیت استفاده کنیم ولی بزار یه کاری کنیم، بیاییم بگیم اون Prover ما یه پیام رو هم توی محتویاتی که هش میکنه بیاره ! و به این شکل کلا فرایند ما عوض شد

به شکل ساده تری توضیح بدم :

توی حالت interactive فرایند اینطوریه :

Prover → Verifier: Sends a commitment (e.g., R=gr)
Verifier → Prover: Sends a random challenge (e.g., c)
Prover → Verifier: Sends a response (e.g., s=r+c⋅x)

ولی توی مدل اقای Fiat–Shamir که Non-Interactive عه این شکلیه :

فقط و فقط Prover میاد تمام اجزا رو میچینه کنار هم و ازشون هش میگیره ، Verifier هیچ کاری نمیکنه ، ن پیام میده ن کاری میکنه، تا وقتی که Prover هش رو بفرسته و Verifier اونجا هش رو چک میکنه

یعنی Prover هش میگیره:

c=HASH(R,msg)

و جواب رو حساب میکنه :

s=r+c⋅x

اینجا هش همون c عه ، و در نهایت Prover اینو میفرسته به سمت Verifier :

(msg,R,s)

که R میشه g^r که به زبان ساده میشه یه عدد رندوم یا همون nonce خودمون ، msg که میشه متنی که اضافه کردیم (هرچی) و s که میشه حاصل معادله اصلی + هش

🔸نکته : پیامی که اضافه شده فقط جهت محکم کاریه و چیز خیلی خاصی نیست

🔸نکته : مقدار R

🔸نکته : سمت راست ما دیگه پروتوکل Schnorr نداریم، بلکه بهش میگن امضای Schnorr !

🔸نکته : در اینجا به این نکته میرسیم که ما امضای دیجیتال داریم به یه نوعی ، نه؟ درسته :) به پروتوکل های ZKP ای که interactive نباشن میگن digital signature :

digital signatures are just non-interactive zero-knowledge proofs

🔸7.3 The signature algorithms you should use (or not)

قراره نویسنده اینجا به ما بگه کدوم الگریتم امضای دیجیتال خوبه و کدوم بده (امن نیست)

اگر دو فصل قبل رو خونده باشید میدونید که ما درباره تبادل کلید صحبت کردیم ، ریاضیات الگریتم های امضای دیجیتالم بر اساس اون هاست ! یا بر اساس عداد صحیح (RSA, DSA) یا بر اساس منحنی بیضوی (ECDSA, EdDSA)

از لحاظ تاریخی هم اول تو سایت 1977 که RSA امده بود گفتن خب دیگ امضای دیجیتال داریم و RSA رو برای این کار استفاده میکردن :

Public key: e,n
Private key: d
Signature: s=m^d mod n

ولی توی سال 1991 NIST امد یه الگریتم جدا برای امضای دیجیتال زد به اسم :Digital Signature Algorithm (DSA)

از اونجایی که NIST امریکاییه پس DSA مال امریکاس ، ریاضیات این الگریتم مثل الگریتم Schnorr عه، فقط بخاطر بحث patent و اینا امدن اسمشو عوض کردن و ی تغییر کوچولو تو ریاضیاتش دادن و ثبتش کردن، و وقتی publish اش کردن هیچ Proof یا سندی ارائه ندادن که امنه و حقیقتا هیچکسیم نیامد امنیتشو نقض کنه ، با اینکه امنیت الگریتم خوب بود و خیلیا ازش استفاده میکردن ولی سریع با ورژن منحنی بیضویش جایگزین شد ECDSA (for Elliptic Curve Digital Signature Algorithm) و تعجیبیم نداره چون الگریتم Diffie-Hellman (DH) با ورژن بیضویش (Elliptic Curve Diffie-Hellman (ECDH))

وقتی patent امضای Schnorr signatures توی سال 2008 منقضی شد، خالق ChaCha20-Poly1305 (فصل4 گفتمش) و X25519 (فصل 5 گفتمش) آمد گفت من یه طرح جدید دارم به اسم EdDSA (for Edwards-curve Digital
Signature Algorithm) که دقیقا بر اساس Schnorr signatures هست، و خیلی محشره و خیلیام سریع قبولش کردن و مطرح شد

در ادامه اول الگریتم RSA رو قراره بررسی کنیم، بعد ECDSA و بعدشم EdDSA

🔸7.3.1 RSA PKCS#1 v1.5: A bad standard

چون اولین الگریتم امضای دیجیتالی ک امد با RSA کار میکرد و همه هم سریع ازش استفاده کردن، خیلی مطرح شد و با وجود مشکلاتی که داره (جلوتر بهش میرسیم)، نباید ازش استفاده کرد، ولی چون تغییر نرم افزاری زمان بر و سخته، قراره خیلی جاها شاهدش باشید :)

یادتونه با RSA چطوری رمز میکردیم؟ امضاش دقیقا برعکسشه :

برای رمز با Public Key رمز میکردن برامون و با Private Key از رمز در میاوردیم و میخوندیم

برای امضا با Private Key امضا میکنیم و بقیه با Public Key امضای مارو اعتبار سنجی میکنن

🔸نکته : در عمل، قبل اینکه یه پیام بخواد امضا بشه، اول تبدیل به Hash میشه و فضای کمتری رو میگیره به عنوان ورودی، و از اونجایی ک میدونیم اندازه بلاک ورودی RSA یکسانه با Modulus اش (کلیدش)، پس اینطوری شانس امضای یک تیکه متن بیشتره، و معمولا جواب این امضا خیلی بزرگ تر از حد معمول ساخته میشه چون در برخی از اعمال ریاضی به امضای بزرگ نیاز دارن

توی عکس زیر این عمل نشون داده شده، قبل کار بگم که کلید عمومی رو e گرفته و کلید خصوصی رو d و n هم که بخش پذیر یا modulus مونه :

برای امضا :

signature = message^d mod N

برای اعتبار سنجی :

signature^e mod N = message

فقط کسی که به کلید خصوصی یا d دسترسی داره میتونه امضا رو محاسبه کنه، و از اونجایی ک ما داریم با الگریتم RSA کار میکنیم و امنیت RSA وابستس به بحث factorization problem ، امنیت این امضا هم وابسته به اونه

از چه استانداردی استفاده کنیم برای RSA ؟ توی فصل 6 که گفتیم استاندارد رمزنگاری RSA رو ، استاندارد RSA PKCS#1 v1.5 رو بررسی کردیم که درباره امضا با RSA هم صحبت کرده، برای امضا اول باید پیام هش بشه با الگریتمی ک خودمون میخوایم، ادامش پد بشه تا سایز پر بشه و با کلید خصوصی رمز بشه :

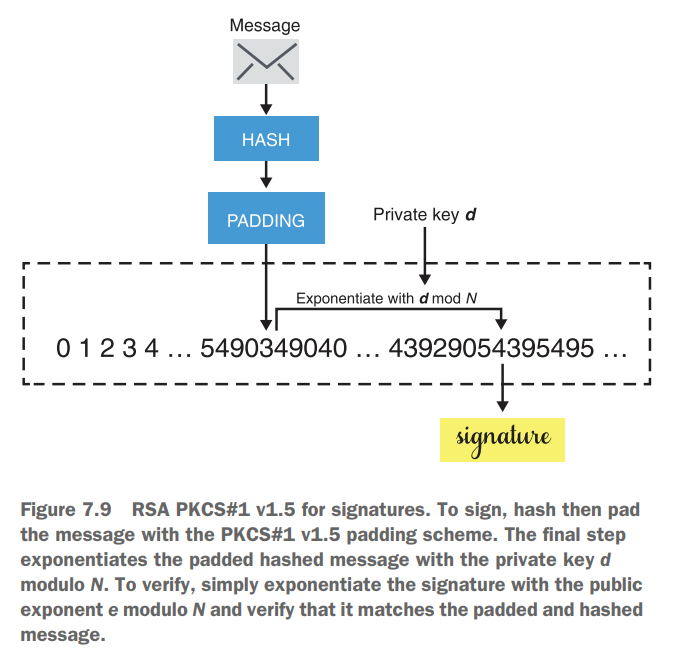
توی عکس بالا یه نکته تقریبا مهمی رو درباره اسامی RSA میبینیم، ما یه شرکت به اسم RSA داریم که موقع تاسیس خود پروتوکل زده شده و سازنده های پروتوکل زدنش که بحثش جداست، یکی خود الگریتم رمزنگاری RSA رو داریم و یکیم الگریتم امضای RSA رو ، وقتی میگیم میخوایم با RSA رمز کنیم منظورمون این ک ما به RSA PKCS#1 v1.5 یا RSA-OAEP اشاره میکنیم ، ولی وقتی میگیم میخوایم با RSA امضا کنیم ، ما به RSA PCSK#1 v1.5 و RSA-PSS اشاره میکنیم

اگر تا الان گیج نشدید باید بگم شما خیلی خارق العاده اید 😂 چون ملت گیج شدن و نفهمیدن چرا استاندارد PCSK#1 v1.5 برای دوتاش باید یه نام داشته باشه و در نهایت امدن گفتن خب اسم پروتوکل رمزنگاری میشه PCSK#1 v1.5 و مال امضاش میشه RSASSA-PKCS1-v1_5
واقعا مغز رنده کن 😂😂😂

حملات RSA :

تو فصل 6 داشتیم حملاتشو ، ولی نکته جالب اینجاس ک ی اقایی ب اسم Bleichenbacher که سال 1998 امد حمله کشف کرد روی RSA PKCS#1 v1.5 ، مصمم شد از ورژن امضا دیجیتالشم باگ دربیاره که رفت و سال 2006 امد با ی حمله برگ ریزون به نام جعل امضا (signature forgery) روی همون استاندارد RSA PKCS#1 v1.5

این حمله یه نوع حمله به نحوه پیاده سازی الگریتم بود

🔸نکته : فرق بین حمله به پیاده سازی یک الگریتم رمزنگاری (implementation attack) و حمله به خود الگریتم رمزنگاری اینه ک در دومی کلا الگریتم نقض میشه و میرن سراغ یکی دیگه ولی توی اول میرن ببینن کجا اشتباه پیاده سازی کردن و درستش میکنن ( توی کد لایبرری هر زبان برنامه نویسی که میخوان بررسی کنن)
و حمله ای ک اقای Bleichenbacher روی خود الگریتم RSA کشف کرده بود مال خود الگریتم بود ولی اونی ک برای امضاش کشف کرده بود مربوط ب پیاده سازی بود که اگر درست پیاده سازی بشه قابل رفع هست.
و تا 2019 امدن کلی از لایبرری ها و.. رو نگاه کردن و دیدن ای بابا ، تقریبا خیلیاشون مشکل پیاده سازی دارن و به فکر یه چیز دیگه باید باشن ، چون تقریبا در همه موارد امکان اجرای حمله signature forgery بود !

🔸7.3.2 RSA-PSS: A better standard
یه استاندارد جدیدی برای امضای دیجیتال با RSA امد به اسم PKCS#1 v2.1 و اسم الگریتمش RSA-PSS هست که با Proof of Security امد (یک ادله امنیتی داره که PKCS#1 v1.5 نداشت)، حالا فرقش چی بود؟

اول پیام رو با الگریتم PSS انکود میکنه

دوم پیام انکود شده رو با RSA امضا میکنیم (این قسمتش مثل استاندارد PKCS#1 v1.5 هست)

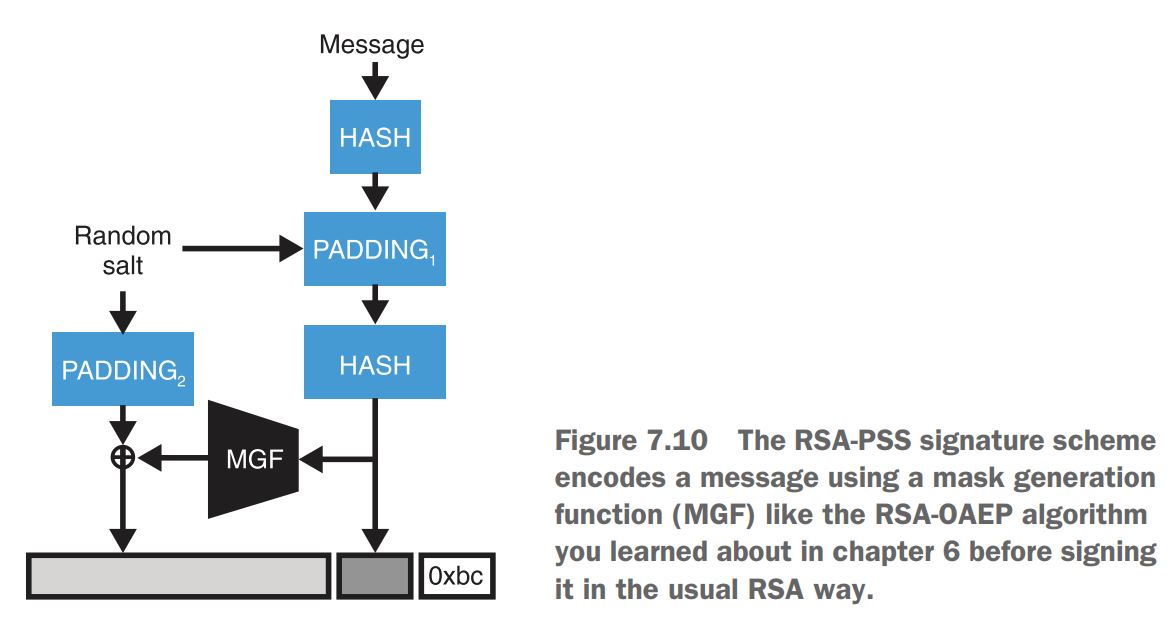
توضیح عکس : اول از پیام هش میگیرن -> یه salt رندوم اضافه میشه به پدینگ -> این پدینگ + هش به یه بلوک واسط تبدیل میشه -> با تابع Mask Generation Function (MGF) دوباره همه چی تصادفی میشه -> یه لایه دیگه پدینگ به اسم پدینگ 2 اضافه میشه به نتیجه اون تابع -> یه بایت مشخص "0xbc" به ته کار اضافه میشه و طبق بلوک های خاکستری ک میبینید نتیجه ساخته میشه

اعتبار سنجی چطوریه؟ دقیقا برعکس کاره، چطوری؟ اول امضارو به توان e ماد n میکنه : ^e mod N و بعد انکودینگ رو برعکس انجام میده

توضیح عکس بالا : فرض کنید یه قصر دارید و یه پادشاه، پادشاه توی یه اتاق سنگی توی قصره ، در اتاق پادشاه قفل داره و در قصر هم قفل داره، بنظرتون اگر کسی بتونه در اتاق پادشاه رو بشکنه ، میتونه حتما در قصرم بشکنه؟؟ نه! چرا؟ چون در قصر خیلی محکم و قویه !! ولی در اتاق پادشاه نهایتا یه قفلی چیزی داشته باشه ! پس ما میگیم کسی که در قصرو شکسته ، حتما میتونه در اتاق پادشاه رو بشکنه ، چون در قصر خیلی قوی تر از در یه اتاقه ! به این سبک میگن contrapositive proof style یا سبک اثبات عکس (یا سبک اثبات نقض) و برای الگریتم RSA-PSS اینطوریه که چون با PSS ما امدیم یه سبک جدید از الگریتم امضا ساختیم که ترکیب RSA و PSS عه ، به طبع اگر کسی اینو بشکنه ما میگیم خب الگریتم RSA معمولی رو که حتما میتونه بکشنه ! و نکته اخر اینه که چه الگریتم RSA-PSS و چه خود الگریتم RSA اگر قرار باشه مورد ازمایش قرار بگیرن ، تنها رکن اصلی که باید مورد ازمایش قرار بگیره ، امنیت خود RSA عه ! پس در نهایت ما میگیم RSA-PSS متکیه بر امنیت RSA

(این دوتا جمله رو قاطی نکنید ، امنیت RSA-PSS مبتنی و متکیه بر امنیت RSA ولی اگر قرار باشه بگیم کدوم سخت تر شکسته میشه، به طبع RSA-PSS چون یه لایه اضافه تر داره ، و اگر با وجود یه لایه اضافه تر شکست بخوره پس طبعا خود RSA که معمولی هم شکست میخوره)

توی بحث RSA که فصل 6 داشتیم ، از الگتریم RSA-KEM هم اسم بردیم که خیلی معروف نیست ولی امنه ولی با این حال خیلیا ازش استفاده نمیکنن !! و امدن یه الگریتم امضای دیجیتال با این هم ساختن به اسم Full Domain Hash (FDH) که مثل مابقی الگریتم ها میاد اول پیام رو هش میکنه و بعد اون هشو امضا میکنه ( منتها فرقی که داره اینه که اینجا وقتی هش انجام شد، اون هش تبدیل به عدد میشه )

🔸آقای وونگ میزنه تو سر خودش که چرا همش از RSA معمولی براش هش استفاده میکنید (استانداردPKCS#1 v1.5 ) و میگه این امن نیست برید حداقل از این دوتا استفاده کنید 🙆‍♂️

🔸7.3.3 The Elliptic Curve Digital Signature Algorithm (ECDSA)

میرسیم به ورژن منحنی بیضوی DSA که برای جلوگیری از ثبت اختراع امضای Schnorr امد، و توی خیلی از استندارد ها هم هست : ISO 14888-3, ANSI X9.62, NIST FIPS 186-2, IEEE P1363

و کسایی که میخوان استفاده کنن باید سر استانداردی که انتخاب میکنن به توافق برسن چون استاندارد ها باهم منطبق نیستن !

و بر عکس Schnorr ، که اثبات امنیت داشت (Proof of Security) ، ولی ECDSA اصلا اثبات امنیتی نداره و با این حال خیلی هم ازش استفاده میشه

قبل ادامه من ضرب اسکالر یا scalar multiplication و نقطه پایه ی G رو خیلی ساده توضیح بدم :

به زبان ساده ما یک بردار یا یک ماتریس (همین خط هایی که کشیدن و توش به صورت عمودی و افقی عدد نوشتن ، مثلا 3 و 7 و 9 و 10 الان روی همن و دورشون خط ][ کشیدن، بهش میگن ماتریس) رو در یک عدد که بهش میگن اسکالر ضرب میکنیم، یعنی تک تک اعداد ماتریس رو در اسکالر ضرب میکنیم

نقطه G چیه؟ بهش میگن نقطه پایه یا Base Point یا G ، روی هر منحنی بیضوی یک نقطه انتخاب میشه که ازش به عنوان یک عامل پایه برای ساختن اعداد ( Generator Point ) استفاده میشه، این نقطه روی منحنی یه مشخصات x و y داره ، این گروه با خودش جمع میشه (عملیات جمع روی منحنی) و اینطوری کل گروه نقاط تولید میشه.

حالا توی این الگریتم منحنی بیضوی(ECDSA)، کلید ها چطوری ساخته میشن ؟

کلید خصوصی : یه عدد رندوم خیلی بزرگ (فرض کنید x کوچک)

کلید عمومی : از ضرب اسکالر x که خط بالا گفتم با نقطه G (یعنی G رو با خودش اندازه x بار جمع میکنیم) (فرض میکنیم X بزرگ)

X = x * G

اینجا ضرب روی منحنی بیضوی انجام میشه

چیز خاصی نمیگه عکس بالا، فقط میگه اگر یه جا دیدید نوشتن کلید عمومی فرمولش [x]G اینه یا G^x بدونید فرقی نداره و جفتش یکیه

فرایند امضای دیجیتال با الگریتم ECDSA :

پیام رو هش میکنیم H(m)
کلید خصوصی داریم x
یه random nonce داریم ک بهش میگیم k و باید برای هر امضا منحصر به فرد باشه ( اگر k تکرار یا قابل پیش‌بینی باشه کلید خصوصی لو میره)

امضا ما دو قسمت داره :

r = x-coordinate of (k * G) و s equals k–1 (H(m) + xr) mod p

بریم یکم ساده تر توضیحشون بدم :

براتون روی تخته نقاشی کشیدم :) ، اول میاییم از پیام هش میگیریم و اسمشو میزاریم Z ، این هش میتونه مثلا با SHA-256 باشه (اگر طول هش بیشتر از طول بیت‌های منحنی باشه، کوتاه میشه)

بعد یه نقطه روی منحنی انتخاب میکنیم، این نقطه یه مشخصه x داره و یه y ، ما فقط x شو لازم داریم، حالا با k که داریم ضرب میکنیم

حالا قسمت اول امضا : میاییم بردار x مال R رو mod میکنیم با P (اگر r = 0، باید k جدید انتخاب کنیم)

برای محاسبه قسمت دوم : K ای ک داشتیمو برعکس میکنیم و ضرب میکنیم در حاصل (امضا + ضرب قسمت اول امضا در کلید خصوصی) و mod P میشه

اول r و بعد s میشه امضامون

حالا اعتبار سنجی امضا :

ورودی‌ها:
هش پیام H(m)
کلید عمومی X
امضا (r, s)
[H(m) s⁻¹] G + [r s⁻¹] X

مختصات x نقطه به دست اومده باید برابر r باشه، اگر برابر بود پس امضا معتبره

🔸نکات خیلی مهم :

k نباید تکراری یا قابل پیش‌بینی باشه.

اگر k فاش یا دوباره استفاده بشه پس کلید خصوصی x لو میره.

ما اینجا ب k گفتیم nonce ، هر جا شنیدید nonce بدونید فقط قراره یبار از این عدد استفاده بشه! و تمام !

اقای وونگ میفرمایند خیلی از جاها k رو پشت صحنه حساب میکنن ولی خیلی جاها از کاربر k رو میگیرن که باعث بدبختی میشه :)) مثلا درسال 2010 روی پلیستیشن 3 ، nonce های تکراری دیده شد که منجبر به افشای کلید خصوصیش شد (چند بیت k هم لیک بشه باز میشه کلید خصوصی رو پیدا کرد ، و به حملاتش میگن lattice attacks ، چنین حملاتی باعث میشه کاملا الگریتم شکست بخوره و خیلی وحشتناکه !)

راه حل چیه؟ امدن گفتن ما ی کاری کنیم nonce طبق کلید خصوصی و پیام ساخته بشه و توی RFC 6979 این امد و مشکل حل شد، یعنی اگر یک پیام بخواد دوبار امضا بشه ، k تکراری میشه ولی مشکلی نیست چون همون پیامه !

منحنی های بیضوی ای میخواستن توی بحث امضای دیجیتال استفاده بشن، تقریبا همونایین که توی بحث Elliptic Curve Diffie-Hellman استفاده شدن (فصل 5 رو بخونید اگر نمیدونید چی میگم) ، ولی یه استثنا ریز هست و اونم Secp256k1 هست، وقتی بیتکوین تصمیم گرفت بجای منحنی های NIST که توی فصل 5 بررسی کردیم بره سراغ Secp256k1 ، خیلی مشهور شد

منحنی Secp256k1 از نوع منحنی های Koblitz هست که پارامتر های ورودیش محدودیت دارن و باعث میشه در پیاده سازی ما بهینه تر نتیجه ببینیم (به زبان ساده یعنی پارامتراش ساده تر میشن)

معادلش اینه :

y² = x³ + a x + b

که a = 0 و b = 7 همیشه همینن

و x و y این منحنی روی اعداد به mod P تعریف میشن :

p = 2192 – 232 – 212 – 28 – 27 – 26 – 23 – 1

حالا گروه و نقطه پایه منحنی secp256k1 چطوریه ؟

تعداد نقاط منحنی (Order):

توی secp256k1 تعداد کل نقاطی که روی منحنی هست یه عدد اول خیلی بزرگه :

n = 115792089237316195423570985008687907852837564279074904382605163141518161494337

این n در واقع Order گروهه، یعنی اگر نقطه پایه G رو n بار با خودش جمع کنیم، به نقطه بی‌نهایت می‌رسیم.

نقطه پایه (Generator Point) :

G نقطه‌ایه که کل گروه رو تولید می‌کنه و مختصاتش روی منحنی secp256k1 مشخصه

G.x = 55066263022277343669578718895168534326250603453777594175500187360389116729240
G.y = 32670510020758816978083085130507043184471273380659243275938904335757337482424

چرا این نقطه انتخاب شده؟

G باید ویژگی‌های زیر رو داشته باشه:

روی منحنی باشه
Order اول بزرگ داشته باشه (برای امنیت)
بتونه کل گروه رو تولید کنه

و در نهایت گرچه بیت‌کوین از secp256k1 استفاده می‌کنه،
ولی ECDSA معمولاً با منحنی NIST P-256 استفاده میشه

🔸7.3.4 The Edwards-curve Digital Signature Algorithm (EdDSA)

اخرین الگریتم امضای دیجیتالی که میخوایم بررسی کنیم به منحنی ادوارد معروفه و بخاطر بی اعتمادی ای که به NIST هست ساخته شده، اقای Daniel J. Bernstein سال 2011 این الگریتمو معرفی کردن

اسم EdDSA رو اگر بشنوید ممکنه فک کنید مثل ECDSA عه ولی اشتباه میکنید، بر اساس امضای Schnorr Signature ساخته شده

EdDSA برخلاف ECDSA که به k برای هر عملیاتش نیاز نداره ، میاد خودش بر اساس هش و پیام k رو میسازه، این باعث میشه مشکل تکرار k (که تو ECDSA باعث لو رفتن کلید خصوصی میشد) دیگه اینجا مشکل ساز نباشه!

این الگریتم خیلی مورد استقبال قرار گرفت و ازش استفاده شد و توی خیلی از پروتوکل ها و استاندارد ها قرار گرفت

الگریتم EdDSA داره میره که توی استاندارد NIST ثبت بشه (FIPS 186-5) و استاندارد فعلی که داریم تحت عنوان RFC 8032 دوتا منحنی داره با لول های امنیتی متفاوت که EdDSA ازشون استفاده میکنه ، به جفتشون میگیم Twisted Edwards Curves یا منحنی های پیچ خورده ادواردز 😂😂 این منحنی ها به شکلین که جمع و ضرب توشون ساده تره :

Edwards25519

بر پایه Curve25519 که Bernstein ساخته، سریع و امنه و کلید عمومی روی همین منحنی تولید میشه.

Edwards448

بر پایه منحنی Ed448-Goldilocks ساخته شده ، امنیت 224 بیت میده ، قوی‌تره ولی کندترم هست

به Edwards25519 میگن Ed25519 و به Edwards448 هم میگن Ed448 و این اسم مختصر گیجتون نکنه.

نحوه ساخت کلید توی EdDSA متفاوته ، بجایی ساخت مستقیم یه کلید برای امضا، میاد یه secret key میسازه و از اون دوتا کلید درمیاره که یکیش میشه کلید امضا و دومیش میشه nonce key

🔸نکته : آقای وونگ گفت حواستون باشه که وقتی میخواد توی لایبرری های مختلف از کلید های مختلف استفاده کنید، بدونید 32 بیته یا 64 بیت ! این مهمه !

فرآیند امضای EdDSA :

EdDSA شبیه Schnorr عمل می‌کنه

nonce = HASH(nonce key || message)

اول میاد اون nonce key رو با پیام هش میگیره و به یه nonce میرسه، بعد :

R = nonce * G
h = HASH(R || public key || message)
s = nonce + h * signing key

و به یه R و s میرسیم

اعتبار سنجی امضا :

اول s * G محاسبه میشه و بعد R + h * public key

اگر این دو برابر بودن یعنی امضا معتبره .

اگر نمیدونستید بدونید که Ed25519 معروف ترین نسخه EdDSA هست و معادلش اینه :

–x2 + y2 = 1 + d × x2 × y2 mod p

که d یه مقدار بزرگیه : 37095705934669439343138083508754565189542113879843219016388785533085940283555
و p میشه عدد اول بزرگ ، و دوتا نقطه پایه :
G.x = 15112221349535400772501151409588531511454012693041857206046113283949 847762202
G.y = 46316835694926478169428394003475163141307993866256225615783033603165 251855960

حالا

انواع مختلف Ed25519:

استاندارد RFC 8032 سه نسخه معرفی می‌کنه:

Ed25519: نسخه اصلی (همینی که الان گفتم)
Ed25519ctx: یه string یا رشته اجباری میگیره و امنیتو بیشتره میکنه
Ed25519ph: پیام قبل از امضا هش میشه (Pre-hash)

اگر خاطرتون باشه ما از customization string یا رشته اجباری توی فصل 2 استفاده کردیم و یا در فصل 8 برای key derivation function هم ازش استفاده میکنیم و کجا به کار میاد؟ وقتی کاربر ها میخوان پیام های مختلفی رو با کلید های خصوصیشون امضا کنن، یعنی مثلا ی اپلیکیشن هست که به کاربر ها میگه میتونی پرداخت هاتو امضا کنی و تو با کلید خصوصی امضا میکنی ، و همچنین میگه تو میتونی پیام هایی که توی اپلیکیشن میدی به بقیه هم با همون کلید خصوصی امضا کنی، اینجا مشکلی که هست چیه؟ فک کن مثلا یه پیام رو امضا میکنی که خیلی شبیه پرداخته ، و اون میتونه به همه بگه بیایید ببینید این چه پرداختی رو امضا کردههههه😳😐 و سر همین بهتره بریم سراغ Ed25519ph

🔸7.4 Subtle behaviors of signature schemes

بعضی ویژگی‌های ظریف توی الگوریتم‌های امضا هستن که ممکنه مشکل‌ساز بشن، توی بیشتر پروتکل‌ها شاید مهم نباشه، ولی وقتی پروتکل‌های پیچیده‌تر یا غیرمعمول طراحی میشن، می‌تونن دردسرساز بشن.

🔸 7.4.1 Substitution attacks on signatures

سخن بزرگان : یک امضای دیجیتال همیشه به‌طور یکتا یک کلید یا یک پیام رو مشخص نمی‌کنه. یعنی چی؟

ما یه حمله داریم به اسم جایگزینی (Substitution attacks) که بهش duplicate signature key selection (DSKS) هم میگن و روی دوتا امضای اول که بررسی کردیم یعنی DSA و RSA-PSS اجرا میشه و دو نوع داره :

: Key substitution attacks
کلید عمومی یا جفت کلید متفاوتی برای اعتبارسنجی یک امضای موجود استفاده میشه ، یعنی همون امضا روی همون پیام، ولی کلید عوض میشه
: Message key substitution attacks
کلید عمومی جدید و پیام جدید انتخاب میشه که امضای قدیمی رو معتبر نگه می‌داره، یعنی: امضا ثابت میمونه، ولی پیام تغییر می‌کنه

پس فرقشون شد : توی اولی پیام و امضا ثابت میمونه و فقط کلید عوض میشه ولی توی دومی امضا ثابت میمونه ولی پیام عوض میشه و کلید جدید ساخته میشه

زیاد حال توضیح ندارم ولی به صورت خلاصه : این حملات به‌خاطر شکاف بین تئوری و پیاده‌سازی هست، یعنی مهاجم می‌تونه پیام‌هایی رو انتخاب کنه و از امضاکننده بخواد امضا کنه، حالا هدف مهاجم چیه؟ پیدا کردن یک پیام جدید با امضای معتبر که قبلاً امضا نشده.

Normal signature: پیام و امضا با کلید اصلی بررسی میشه پس معتبره
Key substitution attack: پیام و امضا ثابت، کلید جدید ساخته میشه که امضا رو معتبر می‌کنه
Message key substitution: پیام جدید، کلید جدید، امضای قدیمی همچنان معتبره

🔸7.4.2 Signature malleability

فوریه ۲۰۱۴، MtGox، یکی از بزرگ‌ترین صرافی‌های بیت‌کوین، بسته شد و اعلام ورشکستگی کرد چون مهاجمان با حملات malleability حساب‌ها را خالی کردند.
— کریستین دکر و راجر واتنهوفر

بیشتر الگریتم های امضای دیجیتال شکل پذیر یا malleable هستن، یعنی اگر شما به من یک امضای دیجیتال معتبر بدید من میتونم اونو دستکاری کنم و به یه امضای دیجیتال معتبر دیگه تبدیلش کنم، مطمئنا نمیدونم این امضا برای چیه ولی تونستم امضای جدید و معتبری بسازم !

عدم شکل پذیری یا Non-malleability به معنی این نیست که امضاها یکتا و خاص باشن، من امضا کننده میتونم چند امضای متفاوت برای همون یه پیامی که دارم بسازم و این بد نیست ، ولی بعضی جاها به این مورد که من نیازه امضاهام تفاوت داشته باشن نیاز دارن که اگر میخواید پروتوکل بسازید باید حواستون به اینا باشه

یه مدل جدید داریم به اسم EUF-CMA که برای مقاومت دربرابر شکل پذیری یا malleable ساخته شده و استاندارد های جدید مثل RFC 8032 (Ed25519) که ازشون صحبت کردیم هم این مدل رو دارن

حالا چون این قابلیت توی همه کتاب خونه ها نیست، نباید موقع طراحی پروتوکل یا استفاده ، فرض رو بر این بزارید که امضا ها یکتا نیست و ما امنیم و دسخوش حمله شکل پذیری (malleable) نمیشیم