اطلاعات تازه، شانس بیشتر: تفسیر بیزی معمای مونتی هال

در تاریخ علم، گاهی یک مسئله‌ی ساده‌ی سرگرمی یا تلویزیونی به نقطه‌ی عطفی در فهم انسان از احتمال و تصمیم‌گیری تبدیل شده است. یکی از مشهورترین این مسائل، مسئله‌ی مونتی هال (Monty Hall Problem) است که نام خود را از مجری آمریکایی یک مسابقه‌ی تلویزیونی به نام Let’s Make a Deal گرفته است. این مسئله در ظاهر ساده به نظر می‌رسد، اما پاسخ آن بسیاری از شواهدهای ما درباره‌ی احتمال را به چالش می‌کشد. زندگی ما پر است از تصمیم‌هایی که باید در شرایط عدم قطعیت گرفته شوند. گاهی یک انتخاب اولیه داریم، اما با ورود اطلاعات جدید، محاسبات و تصمیم‌گیری‌های ما تغییر می‌کند. مسئله‌ی مونتی هال نمونه‌ای ساده اما عمیق از این وضعیت است و با استفاده از قاعده‌ی بیز (Bayes’ Rule) نشان می‌دهد که هر بار اطلاعات تازه وارد شود، باید شانس‌ها را بازنگری کنیم.

معمای مونتی هال

فرض کنید در یک مسابقه شرکت کرده‌اید. سه درب بسته در مقابل شماست: پشت یکی از درها یک ماشین (جایزه اصلی) و پشت دو در دیگر بز (اشیای بی‌ارزش) قرار دارد. روند بازی به این صورت است:

• شما یکی از سه در را انتخاب می‌کنید.

• مجری مسابقه، که می‌داند پشت هر در چه چیزی است، یکی از دو در باقی‌مانده را باز می‌کند و همیشه یک بز را نشان می‌دهد.

• حالا شما می‌توانید انتخاب اولیه‌ی خود را حفظ کنید یا با در دیگر تغییر دهید.

سؤال این است: بهترین استراتژی چیست؟ ماندن یا تغییر دادن؟

آیا باید روی انتخاب اولیه بمانیم یا با توجه به داده‌های جدید، تصمیم خود را تغییر دهیم؟

تحلیل ریاضی مسئله

بسیاری در نگاه اول تصور می‌کنند که پس از باز شدن یک در، شانس برنده شدن بین دو در باقی‌مانده برابر است (۵۰-۵۰). اما این برداشت اشتباه است.

در ابتدا:

• احتمال اینکه انتخاب اولیه شما ماشین باشد: ۱/۳

• احتمال اینکه ماشین پشت یکی از دو در دیگر باشد: ۲/۳

وقتی مجری یک در را باز می‌کند و یک بز نشان می‌دهد:

• اگر شما ابتدا ماشین را انتخاب کرده باشید (۱/۳ احتمال)، تغییر انتخاب باعث باخت می‌شود.

• اگر ابتدا بز انتخاب کرده باشید (۲/۳ احتمال)، تغییر انتخاب باعث برد می‌شود.

بنابراین:

• احتمال برد در صورت تغییر انتخاب: ۲/۳

• احتمال برد در صورت ثابت ماندن: ۱/۳

به زبان ساده: احتمال اشتباه بودن انتخاب اولیه بیشتر است، پس تغییر دادن انتخاب به نفع شماست.

نتیجه: استراتژی بهینه این است که همیشه انتخاب خود را تغییر دهید.

تفسیر بیزی مسئله مونتی هال

قاعده‌ی بیز (Bayes’ Rule) ابزاری است برای به‌روزرسانی احتمال‌ها بر اساس اطلاعات تازه. به زبان ساده، وقتی داده‌های جدید به دست می‌آوریم، احتمال وقوع یک فرضیه (Hypothesis) را بازنگری می‌کنیم.

فرمول بیزی:

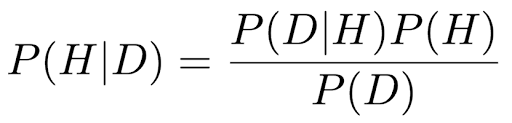
در مسئله‌ی مونتی هال:

• فرضیه‌ها (Hypotheses): ماشین پشت کدام در است؟

• داده (Data): مجری کدام در را باز کرده است؟

• H: فرضیه (مثلاً ماشین پشت کدام در است)

• D: داده یا شواهد تازه (مثلاً مجری کدام در را باز کرده)

• P(H): احتمال پیشین (Prior Probability)

• P(D∣H): شانس مشاهده‌ی داده در صورت درست بودن فرضیه

• P(H∣D): احتمال پسین (Posterior Probability) پس از مشاهده داده

نتیجه‌گیری بیزی از مسئله مونتی هال

مسئله‌ی مونتی هال در ظاهر یک بازی سرگرم‌کننده است، اما با استفاده از قاعده‌ی بیز می‌توان عمق آن را نشان داد و درس‌هایی درباره تصمیم‌گیری در شرایط عدم قطعیت گرفت.

قاعده‌ی بیز به‌طور دقیق نشان می‌دهد که پس از دریافت اطلاعات جدید، احتمال‌ها تغییر می‌کنند:

• انتخاب اولیه شما همچنان با احتمال ۱/۳ درست است.

• اما انتخاب دیگر اکنون با احتمال ۲/۳ درست است.

مجری با باز کردن یک در و نشان دادن بز، اطلاعات تازه‌ای وارد بازی می‌کند و شانس‌ها باید بازنگری شوند. بنابراین تغییر انتخاب شانس برد شما را دو برابر می‌کند.

بنابراین:

انتخاب اولیه همیشه بهترین نیست.

اطلاعات تازه می‌تواند مسیر تصمیم‌گیری را تغییر دهد.

نادیده گرفتن شواهد = ماندن روی شانس پایین.

تغییر آگاهانه = افزایش احتمال موفقیت.

برنده کسی است که با شجاعت تصمیم خود را به‌روز کند و احتمالات را بازنگری نماید.

فراتر از بازی، این موضوع فقط به مونتی هال محدود نمی‌شود و در زندگی واقعی، سیاست، اقتصاد و امنیت کاربرد دارد:

• سرمایه‌گذاری و اقتصاد: انتشار گزارش مالی یا تغییر نرخ بهره باید باعث بازنگری در تصمیم‌های سرمایه‌گذار شود.

• سیاست داخلی و خارجی: موضع جدید یک کشور یا اطلاعات تازه در مذاکرات باید محاسبات را تغییر دهد.

• امنیت و اطلاعات: داده‌های تازه درباره مظنون‌ها یا تهدیدها باید وزن احتمالات را تغییر دهد.

• زندگی روزمره: در پزشکی، هوش مصنوعی و تصمیم‌های شخصی نیز همواره باید شواهد تازه را وارد محاسبات کنیم.