کاربرد قانون اعداد بزرگ در مدیریت ریسک: از بیمه تا کازینو

تصادف و احتمال بخش جدایی‌ناپذیر از زندگی ما هستند. از پرتاب یک سکه ساده گرفته تا قراردادهای بیمه و بازی‌های کازینویی، همه‌جا عنصر شانس دیده می‌شود. آنچه این رویدادهای ظاهراً غیرقابل پیش‌بینی را قابل مدیریت می‌کند، قانون اعداد بزرگ (Law of Large Numbers) است. این قانون بیان می‌کند که وقتی تعداد مشاهدات زیاد می‌شود، میانگین نتایج واقعی به چیزی که در تئوری انتظار داریم نزدیک خواهد شد.

پرتاب سکه و امید ریاضی

برای فهم ساده این قانون، کافی است یک سکه عادلانه را در نظر بگیریم. احتمال آمدن «شیر» برابر با ۰.۵ است. اگر تنها ۱۰ بار سکه بیندازیم، ممکن است ۷ بار شیر و ۳ بار خط بیاید. این نتیجه با مقدار نظری (۵ بار شیر) تفاوت دارد. اما اگر ۱۰ هزار بار سکه را پرتاب کنیم، نسبت شیرها به کل پرتاب‌ها به عدد ۰.۵ نزدیک می‌شود.

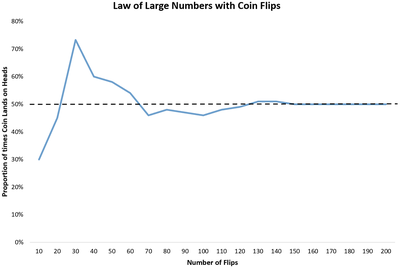
اینجا مفهوم امید ریاضی مطرح می‌شود. امید ریاضی همان میانگین نظری نتایج است. در مثال سکه، امید ریاضی برای احتمال شیر ۵۰٪ است. قانون اعداد بزرگ تضمین می‌کند که هرچه تعداد آزمایش‌ها بیشتر شود، میانگین واقعی به امید ریاضی نزدیک‌تر خواهد شد.

بیمه و تجمیع ریسک

شرکت‌های بیمه دقیقاً از همین اصل استفاده می‌کنند. آن‌ها با جمع‌آوری تعداد زیادی بیمه‌گذار، ریسک را در یک مجموعه بزرگ پخش می‌کنند؛ فرآیندی که به آن تجمیع ریسک گفته می‌شود.

برای مثال، اگر تنها یک خودرو بیمه شود و همان خودرو دزدیده شود، شرکت بیمه دچار زیان بزرگی می‌شود. اما وقتی ۱۰۰ هزار خودرو بیمه شوند، تعداد سرقت‌های سالانه تقریباً به میانگین مورد انتظار نزدیک می‌شود. این پیش‌بینی‌پذیری به شرکت بیمه امکان می‌دهد تا با برنامه‌ریزی مالی و ذخایر کافی، خسارت‌ها را پوشش دهد.

با این حال، بیمه همیشه در معرض رویدادهای غیرمنتظره مانند بلایای طبیعی است. به همین دلیل علاوه بر تجمیع ریسک، بیمه‌گران باید سرمایه و ذخایر اضافی برای پوشش رخدادهای نادر داشته باشند.

کازینو و مزیت ریاضی (House Edge)

در کازینو، سازوکار متفاوتی وجود دارد. اینجا بحث بر سر کاهش نوسان نیست، بلکه طراحی بازی‌ها به گونه‌ای است که کازینو همیشه یک مزیت ریاضی کوچک داشته باشد؛ چیزی که به آن house edge گفته می‌شود. مثلاً در رولت آمریکایی، ۳۸ خانه دارد: (۱۸ قرمز، ۱۸ سیاه، ۲ سبز )، احتمال برد روی قرمز یا مشکی کمتر از ۵۰٪ است. همین تفاوت کوچک (حدود ۵٪) باعث می‌شود که در بلندمدت، بازیکن به طور متوسط مقداری از پول خود را از دست بدهد و کازینو به همان میزان سود تضمین‌شده داشته باشد. وقتی بازی هزاران بار تکرار شود، نوسانات کوتاه‌مدت از بین می‌روند و سود واقعی کازینو به امید ریاضی بسیار نزدیک می‌شود.

این همان چیزی است که کازینوها روی آن حساب می‌کنند: با تعداد زیاد بازی‌ها، اطمینان دارند که سود ثابت خواهند داشت.

نتیجه‌گیری

قانون اعداد بزرگ نشان می‌دهد که در بلندمدت، شانس و تصادف تابع الگوهای قابل پیش‌بینی می‌شوند. پرتاب سکه ساده‌ترین نمونه برای درک این قانون است. بیمه از آن برای تجمیع ریسک و افزایش پیش‌بینی‌پذیری استفاده می‌کند، و کازینو با house edge کوچک ولی دائمی، سود خود را تضمین می‌کند.

به این ترتیب، از سکه‌ای که در دست داریم تا بازی‌های پرزرق‌وبرق کازینو و حتی قراردادهای پیچیده بیمه، همه‌چیز در نهایت به یک اصل بنیادی برمی‌گردد:

اعداد بزرگ، بی‌نظمی و شانس را قابل پیش‌بینی می‌کنند.