مدرس آنالیزداده | یادگیری ماشین | یادگیری عمیق در مجتمع فنی تهران
فصل 17 - ماشین بردار پشتیبان

17.0 مقدمه
برای درک ماشینهای بردار پشتیبان (SVM)، ابتدا باید مفهوم ابرصفحهها را درک کنیم. به طور رسمی، ابرصفحه یک زیرفضای n-1 بعدی در یک فضای n-بعدی است. اگرچه این تعریف ممکن است پیچیده به نظر برسد، اما در واقع بسیار ساده است. برای مثال، اگر بخواهیم یک فضای دوبعدی را تقسیم کنیم، از یک ابرصفحه یکبعدی (یعنی یک خط) استفاده میکنیم. اگر بخواهیم یک فضای سهبعدی را تقسیم کنیم، از یک ابرصفحه دوبعدی (مانند یک ورق کاغذ یا ملافه) استفاده میکنیم. ابرصفحه به سادگی تعمیمی از این مفهوم به n بعد است.
ماشینهای بردار پشتیبان دادهها را با یافتن ابرصفحهای که حاشیه بین کلاسها را در دادههای آموزشی بیشینه میکند، طبقهبندی میکنند. در یک مثال دوبعدی با دو کلاس، میتوانیم ابرصفحه را به صورت پهنترین "نوار" مستقیم (یعنی خطی با حاشیهها) تصور کنیم که دو کلاس را از هم جدا میکند.
در این فصل، به آموزش ماشینهای بردار پشتیبان در موقعیتهای مختلف پرداخته و به بررسی عمیقتر نحوه گسترش این روش برای حل مشکلات رایج میپردازیم.
17.1 آموزش یک طبقهبندیکننده خطی
مسئله
شما نیاز دارید مدلی را برای طبقهبندی مشاهدات آموزش دهید.
راهحل
از یک طبقهبندیکننده بردار پشتیبان (SVC) استفاده کنید تا ابرصفحهای را پیدا کنید که حاشیه بین کلاسها را بیشینه کند.
# Load libraries
from sklearn.svm import LinearSVC
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
import numpy as np
# Load data with only two classes and two features
iris = datasets.load_iris()
features = iris.data[:100,:2]
target = iris.target[:100]
# Standardize features
scaler = StandardScaler()
features_standardized = scaler.fit_transform(features)
# Create support vector classifier
svc = LinearSVC(C=1.0)
# Train model
model = svc.fit(features_standardized, target)بحث
LinearSVC در کتابخانه scikit-learn یک طبقهبندیکننده بردار پشتیبان (SVC) ساده را پیادهسازی میکند. برای درک شهودی از عملکرد SVC، بیایید دادهها و ابرصفحه را ترسیم کنیم. اگرچه SVCها در ابعاد بالا به خوبی کار میکنند، در این راهحل ما تنها دو ویژگی را بارگذاری کردیم و زیرمجموعهای از مشاهدات را انتخاب کردیم تا دادهها فقط شامل دو کلاس باشند. این کار به ما امکان میدهد مدل را به صورت بصری نمایش دهیم. به یاد داشته باشید که SVC تلاش میکند ابرصفحهای را پیدا کند—که در دو بعد یک خط است—که حاشیه بین کلاسها را بیشینه کند. در کد زیر، دو کلاس را در یک فضای دوبعدی ترسیم کرده و سپس ابرصفحه را رسم میکنیم:
# Load library
from matplotlib import pyplot as plt
# Plot data points and color using their class
color = ["black" if c == 0 else "lightgrey" for c in target]
plt.scatter(features_standardized[:,0], features_standardized[:,1], c=color)
# Create the hyperplane
w = svc.coef_[0]
a = -w[0] / w[1]
xx = np.linspace(-2.5, 2.5)
yy = a * xx - (svc.intercept_[0]) / w[1]
# Plot the hyperplane
plt.plot(xx, yy)
plt.axis("off"), plt.show();
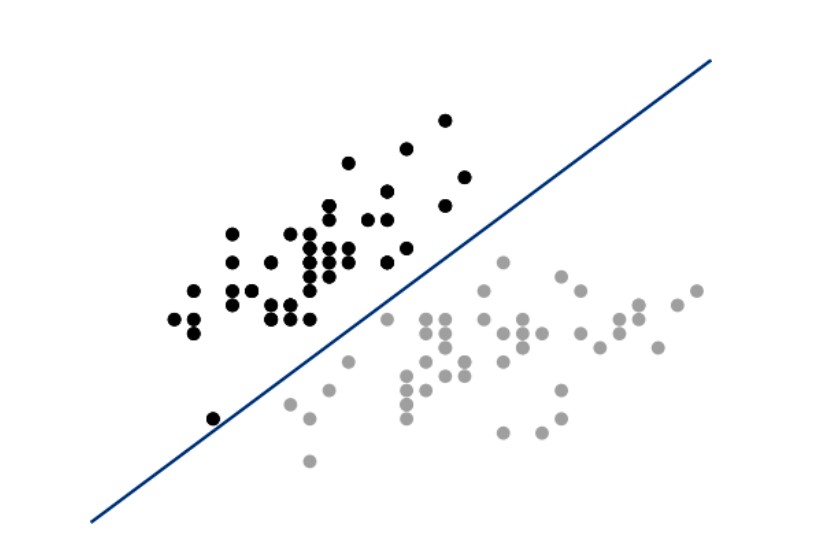
در این نمایش بصری، تمام مشاهدات کلاس ۰ به رنگ سیاه و مشاهدات کلاس ۱ به رنگ خاکستری روشن هستند. ابرصفحه، مرز تصمیمگیری است که مشخص میکند مشاهدات جدید چگونه طبقهبندی میشوند. به طور خاص، هر مشاهدهای که بالای خط باشد به عنوان کلاس ۰ و هر مشاهدهای که زیر خط باشد به عنوان کلاس ۱ طبقهبندی میشود. میتوانیم این را با ایجاد یک مشاهده جدید در گوشه بالا-چپ نمایش بصریمان آزمایش کنیم، که باید به عنوان کلاس ۰ پیشبینی شود:
# Create new observation
new_observation = [[ -2, 3]]
# Predict class of new observation
svc.predict(new_observation)خروجی:
array([0])چند نکته درباره SVCها قابل توجه است. اول، برای سادهسازی نمایش بصری، مثال ما به یک مورد دودویی (یعنی فقط دو کلاس) محدود شد؛ با این حال، SVCها میتوانند با چندین کلاس نیز به خوبی کار کنند. دوم، همانطور که نمایش بصری ما نشان میدهد، ابرصفحه به طور ذاتی خطی است (یعنی منحنی نیست). در این مثال این موضوع مشکلی ایجاد نکرد، زیرا دادهها به صورت خطی قابل تفکیک بودند، به این معنی که یک ابرصفحه میتوانست دو کلاس را به طور کامل از هم جدا کند. اما در دنیای واقعی، این حالت به ندرت پیش میآید.
معمولاً نمیتوانیم کلاسها را به طور کامل از هم جدا کنیم. در چنین موقعیتهایی، تعادلی بین بیشینه کردن حاشیه ابرصفحه و کمینه کردن خطای طبقهبندی وجود دارد. در SVC، این خطا توسط پارامتر C کنترل میشود. C یک پارامتر تنظیمپذیر در SVC است که جریمهای برای طبقهبندی نادرست یک نقطه داده اعمال میکند. وقتی C کوچک است، طبقهبندیکننده با نقاط دادهای که به اشتباه طبقهبندی شدهاند مشکلی ندارد (باعث بایاس بالا اما واریانس پایین میشود). وقتی C بزرگ است، طبقهبندیکننده برای اشتباهات طبقهبندی جریمه سنگینی میپردازد و بنابراین تمام تلاش خود را میکند تا هیچ دادهای به اشتباه طبقهبندی نشود (باعث بایاس پایین اما واریانس بالا میشود).
در scikit-learn، مقدار C توسط پارامتر C تعیین میشود و به طور پیشفرض برابر با ۱.۰ است. باید C را به عنوان یک ابرپارامتر الگوریتم یادگیری در نظر بگیریم و با استفاده از تکنیکهای انتخاب مدل که در فصل دوازدهم بحث شدهاند، آن را تنظیم کنیم.
17.2 مدیریت کلاسهای غیرقابل تفکیک خطی با استفاده از کرنلها
مسئله
شما نیاز دارید یک طبقهبندیکننده بردار پشتیبان را آموزش دهید، اما کلاسهای شما به صورت خطی قابل تفکیک نیستند.
راهحل
از یک ماشین بردار پشتیبان با استفاده از توابع کرنل برای ایجاد مرزهای تصمیمگیری غیرخطی استفاده کنید:
# Load libraries
from sklearn.svm import SVC
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
import numpy as np
# Set randomization seed
np.random.seed(0)
# Generate two features
features = np.random.randn(200, 2)
# Use an XOR gate (you don't need to know what this is) to generate
# linearly inseparable classes
target_xor = np.logical_xor(features[:, 0] > 0, features[:, 1] > 0)
target = np.where(target_xor, 0, 1)
# Create a support vector machine with a radial basis function kernel
svc = SVC(kernel="rbf", random_state=0, gamma=1, C=1)
# Train the classifier
model = svc.fit(features, target)
بحث
توضیح کامل ماشینهای بردار پشتیبان خارج از محدوده این کتاب است. با این حال، توضیح مختصری احتمالاً برای درک ماشینهای بردار پشتیبان و کرنلها مفید خواهد بود. به دلایلی که بهتر است در جای دیگری آموخته شوند، یک طبقهبندیکننده بردار پشتیبان میتواند به صورت زیر نمایش داده شود:
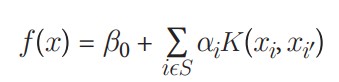
که در آن β0 بایاس است، Ѕ مجموعه تمام مشاهدات بردار پشتیبان، α پارامترهای مدل هستند که باید آموخته شوند، xi و ´xi جفتهایی از دو مشاهده بردار پشتیبان هستند. مهمتر از همه، K یک تابع کرنل است که شباهت بین xi و ´xi را مقایسه میکند. اگر توابع کرنل را درک نمیکنید، نگران نباشید. برای اهداف ما، فقط کافی است بدانید که (1) K نوع ابرصفحهای که برای جداسازی کلاسهای ما استفاده میشود را تعیین میکند، و (2) ما با استفاده از کرنلهای مختلف، ابرصفحههای متفاوتی ایجاد میکنیم. برای مثال، اگر بخواهیم یک ابرصفحه خطی ساده مانند آنچه در دستورالعمل 17.1 ایجاد کردیم داشته باشیم، میتوانیم از کرنل خطی استفاده کنیم:
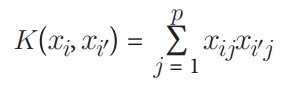
که در آن p تعداد ویژگیهاست. اما اگر بخواهیم یک مرز تصمیمگیری غیرخطی داشته باشیم، کرنل خطی را با یک کرنل پلینومیال جایگزین میکنیم:
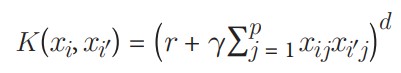
که در آن d درجه تابع کرنل پلینومیال است. به طور جایگزین، میتوانیم از یکی از رایجترین کرنلها در ماشینهای بردار پشتیبان، یعنی کرنل تابع پایه شعاعی (RBF)، استفاده کنیم:
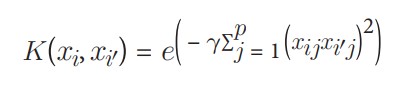
که در آن γ یک ابرپارامتر است و باید بزرگتر از صفر باشد. نکته اصلی توضیحات بالا این است که اگر دادههای غیرقابل تفکیک خطی داشته باشیم، میتوانیم کرنل خطی را با یک کرنل جایگزین کنیم تا یک مرز تصمیمگیری ابرصفحه غیرخطی ایجاد کنیم.
میتوانیم شهود پشت کرنلها را با نمایش یک مثال ساده درک کنیم. این تابع، که بر اساس کاری از سباستین راشکا طراحی شده، مشاهدات و مرز تصمیمگیری ابرصفحه را در یک فضای دوبعدی ترسیم میکند. لازم نیست نحوه کار این تابع را درک کنید؛ من آن را اینجا آوردهام تا بتوانید خودتان آزمایش کنید:
# Plot observations and decision boundary hyperplane
from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
def plot_decision_regions(X, y, classifier):
cmap = ListedColormap(("red", "blue"))
xx1, xx2 = np.meshgrid(np.arange(-3, 3, 0.02), np.arange(-3, 3, 0.02))
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.1, cmap=cmap)
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1],
alpha=0.8, c=cmap(idx),
marker="+", label=cl)در راهحل ما، دادههایی داریم که شامل دو ویژگی (یعنی دو بعد) و یک بردار هدف با کلاس هر مشاهده است. مهم است که کلاسها به گونهای تخصیص داده شدهاند که به صورت خطی قابل تفکیک نیستند. یعنی هیچ خط مستقیمی نمیتوان کشید که دو کلاس را از هم جدا کند. ابتدا، بیایید یک طبقهبندیکننده ماشین بردار پشتیبان با کرنل خطی ایجاد کنیم:
# Create support vector classifier with a linear kernel
svc_linear = SVC(kernel="linear", random_state=0, C=1)
# Train model
svc_linear.fit(features, target) خروجی:
SVC(C=1, kernel='linear', random_state=0) سپس، از آنجا که فقط دو ویژگی داریم، در یک فضای دوبعدی کار میکنیم و میتوانیم مشاهدات، کلاسهای آنها و ابرصفحه خطی مدلمان را نمایش دهیم:
# Plot observations and hyperplane
plot_decision_regions(features, target, classifier=svc_linear)
plt.axis("off"), plt.show();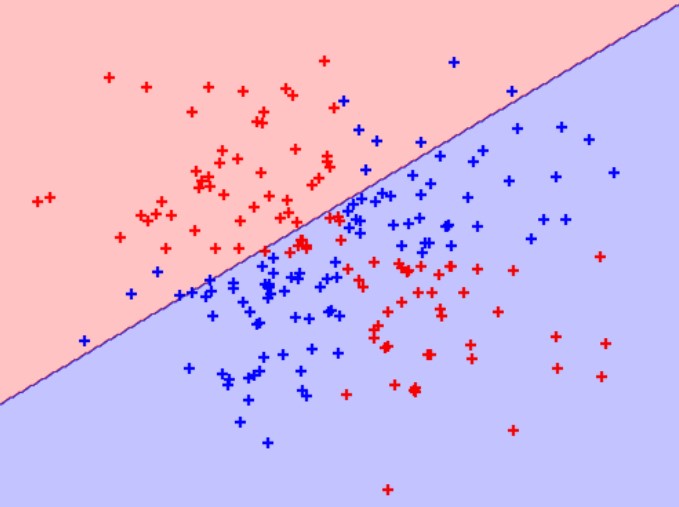
همانطور که میبینیم، ابرصفحه خطی ما در جداسازی دو کلاس عملکرد بسیار ضعیفی داشت! حالا، بیایید کرنل خطی را با یک کرنل تابع پایه شعاعی جایگزین کنیم و از آن برای آموزش یک مدل جدید استفاده کنیم:
# Create a support vector machine with a radial basis function kernel
svc = SVC(kernel="rbf", random_state=0, gamma=1, C=1)
# Train the classifier
model = svc.fit(features, target)و سپس مشاهدات و ابرصفحه را نمایش دهیم:
# Plot observations and hyperplane
plot_decision_regions(features, target, classifier=svc)
plt.axis("off"), plt.show();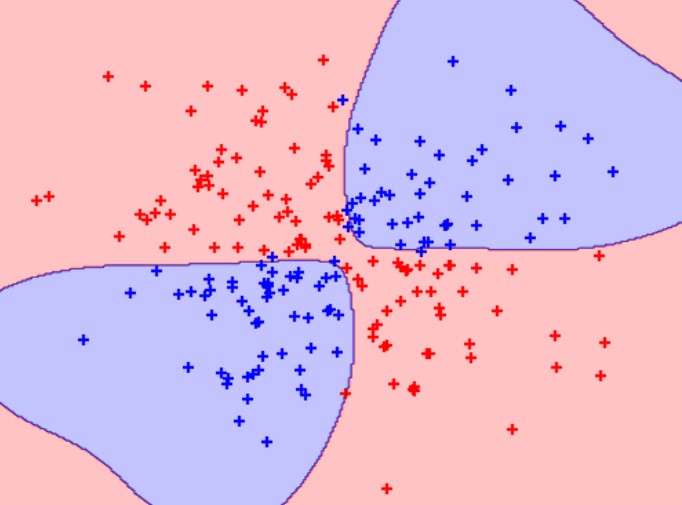
با استفاده از کرنل تابع پایه شعاعی، میتوانیم یک مرز تصمیمگیری ایجاد کنیم که در مقایسه با کرنل خطی، کار بسیار بهتری در جداسازی دو کلاس انجام میدهد. این انگیزه اصلی استفاده از کرنلها در ماشینهای بردار پشتیبان است.
در scikit-learn، میتوانیم کرنلی که میخواهیم استفاده کنیم را با استفاده از پارامتر kernel انتخاب کنیم. پس از انتخاب کرنل، باید گزینههای مناسب کرنل را مشخص کنیم، مانند مقدار d (با استفاده از پارامتر degree) در کرنلهای پلینومیال، و مقدار γ (با استفاده از پارامتر gamma) در کرنلهای تابع پایه شعاعی. همچنین باید پارامتر جریمه C را تنظیم کنیم. هنگام آموزش مدل، در اکثر موارد باید همه اینها را به عنوان ابرپارامترها در نظر بگیریم و از تکنیکهای انتخاب مدل برای شناسایی ترکیبی از مقادیر آنها که مدلی با بهترین عملکرد را تولید میکند، استفاده کنیم.
17.3 ایجاد احتمالات پیشبینیشده
مسئله
شما نیاز دارید احتمالات پیشبینیشده برای کلاسهای یک مشاهده را بدانید.
راهحل
در scikit-learn، هنگام استفاده از SVC، گزینه probability=True را تنظیم کنید، مدل را آموزش دهید، سپس از predict_proba برای مشاهده احتمالات کالیبرهشده استفاده کنید.
# Load libraries
from sklearn.svm import SVC
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
import numpy as np
# Load data
iris = datasets.load_iris()
features = iris.data
target = iris.target
# Standardize features
scaler = StandardScaler()
features_standardized = scaler.fit_transform(features)
# Create support vector classifier object
svc = SVC(kernel="linear", probability=True, random_state=0)
# Train classifier
model = svc.fit(features_standardized, target)
# Create new observation
new_observation = [[.4, .4, .4, .4]]
# View predicted probabilities
model.predict_proba(new_observation)خروجی:
array([[0.00541761, 0.97348825, 0.02109414]])
توضیحات
بسیاری از الگوریتمهای یادگیری نظارتشده که بررسی کردهایم، از تخمینهای احتمالی برای پیشبینی کلاسها استفاده میکنند. برای مثال، در الگوریتم k-نزدیکترین همسایه، کلاسهای k همسایه یک مشاهده بهعنوان رأیهایی برای محاسبه احتمال تعلق آن مشاهده به یک کلاس خاص در نظر گرفته میشوند. سپس کلاسی با بالاترین احتمال پیشبینی میشود. اما در SVC، استفاده از یک ابرسطح برای ایجاد مناطق تصمیمگیری بهطور طبیعی احتمالی برای تعلق یک مشاهده به یک کلاس خاص ارائه نمیدهد. با این حال، میتوان با چند ملاحظه، احتمالات کالیبرهشده را تولید کرد. در SVC با دو کلاس، از مقیاسبندی پلات (Platt scaling) استفاده میشود. در این روش، ابتدا SVC آموزش داده میشود و سپس یک رگرسیون لجستیک جداگانه با اعتبارسنجی متقاطع آموزش داده میشود تا خروجیهای SVC را به احتمالات نگاشت کند:
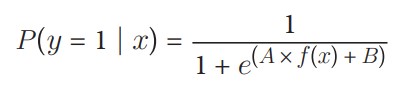
که در آن A و B بردارهای پارامتر هستند و f(x) فاصله نشانشده مشاهده iام از ابرسطح است. برای بیش از دو کلاس، نسخه گسترشیافتهای از مقیاسبندی پلات استفاده میشود.
از نظر عملی، ایجاد احتمالات پیشبینیشده دو مشکل اصلی دارد. اول، به دلیل آموزش یک مدل دوم با اعتبارسنجی متقاطع، تولید احتمالات پیشبینیشده میتواند زمان آموزش مدل را بهطور قابلتوجهی افزایش دهد. دوم، چون احتمالات پیشبینیشده با استفاده از اعتبارسنجی متقاطع تولید میشوند، ممکن است همیشه با کلاسهای پیشبینیشده مطابقت نداشته باشند. بهعنوان مثال، ممکن است یک مشاهده بهعنوان کلاس 1 پیشبینی شود اما احتمال پیشبینیشده برای کلاس 1 کمتر از 0.5 باشد.
در scikit-learn، احتمالات پیشبینیشده باید هنگام آموزش مدل تولید شوند. این کار با تنظیم probability=True در SVC امکانپذیر است. پس از آموزش مدل، میتوان با استفاده از predict_proba احتمالات تخمینی برای هر کلاس را استخراج کرد.
17.4 شناسایی بردارهای پشتیبان
مسئله
شما باید مشخص کنید کدام مشاهدات، بردارهای پشتیبانِ hyperplane تصمیمگیری هستند.
راهحل
مدل را آموزش دهید، سپس از support_vectors_ استفاده کنید:
# Load libraries
from sklearn.svm import SVC
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
import numpy as np
# Load data with only two classes
iris = datasets.load_iris()
features = iris.data[:100,:]
target = iris.target[:100]
# Standardize features
scaler = StandardScaler()
features_standardized = scaler.fit_transform(features)
# Create support vector classifier object
svc = SVC(kernel="linear", random_state=0)
# Train classifier
model = svc.fit(features_standardized, target)
# View support vectors
model.support_vectors_خروجی:
array([[-0.5810659 , 0.42196824, -0.80497402, -0.50860702],
[-1.52079513, -1.67737625, -1.08231219, -0.86427627],
[-0.89430898, -1.4674418 , 0.30437864, 0.38056609],
[-0.5810659 , -1.25750735, 0.09637501, 0.55840072]]) بحث
ماشینهای بردار پشتیبان (SVM) نام خود را از این واقعیت گرفتهاند که hyperplane تصمیمگیری توسط تعداد نسبتاً کمی از مشاهدات، که به آنها بردارهای پشتیبان گفته میشود، تعیین میشود. بهطور شهودی، میتوان تصور کرد که این hyperplane توسط این بردارهای پشتیبان "حمل" میشود. بنابراین، این بردارهای پشتیبان برای مدل ما بسیار مهم هستند. برای مثال، اگر یک مشاهده که بردار پشتیبان نیست را از دادهها حذف کنیم، مدل تغییری نمیکند؛ اما اگر یک بردار پشتیبان را حذف کنیم، hyperplane دیگر حاشیه حداکثری نخواهد داشت.
پس از آموزش یک SVC، کتابخانه scikit-learn گزینههای متعددی برای شناسایی بردارهای پشتیبان ارائه میدهد. در راهحل ما، از support_vectors_ برای نمایش ویژگیهای واقعی مشاهداتِ بردارهای پشتیبان (چهار بردار در مدل ما) استفاده کردیم. بهعنوان جایگزین، میتوانیم ایندکسهای بردارهای پشتیبان را با استفاده از support_ مشاهده کنیم:
model.support_ خروجی:
array([23, 41, 57, 98], dtype=int32) همچنین، میتوانیم از n_support_ برای یافتن تعداد بردارهای پشتیبان متعلق به هر کلاس استفاده کنیم:
model.n_support خروجی:
array([2, 2], dtype=int32) 17.5 مدیریت کلاسهای نامتوازن
مسئله
شما باید یک طبقهبندیکننده ماشین بردار پشتیبان (SVM) را در حضور کلاسهای نامتوازن آموزش دهید.
راهحل
با استفاده از class_weight جریمهی اشتباه در طبقهبندی کلاس کوچکتر را افزایش دهید:
# Load libraries
from sklearn.svm import SVC
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
import numpy as np
# Load data with only two classes
iris = datasets.load_iris()
features = iris.data[:100,:]
target = iris.target[:100]
# Make class highly imbalanced by removing first 40 observations
features = features[40:,:]
target = target[40:]
# Create target vector indicating if class 0, otherwise 1
target = np.where((target == 0), 0, 1)
# Standardize features
scaler = StandardScaler()
features_standardized = scaler.fit_transform(features)
# Create support vector classifier
svc = SVC(kernel="linear", class_weight="balanced", C=1.0, random_state=0)
# Train classifier
model = svc.fit(features_standardized, target)بحث
در ماشینهای بردار پشتیبان، C یک هایپرپارامتر است که جریمهی اشتباه در طبقهبندی یک مشاهده را تعیین میکند. یکی از روشهای مدیریت کلاسهای نامتوازن در ماشینهای بردار پشتیبان، وزندهی به C بر اساس کلاسها است، بهطوری که:
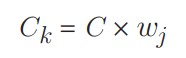
که در آن C جریمهی اشتباه در طبقهبندی است، wj وزنی است که بهصورت معکوس با فراوانی کلاس j متناسب است، و Ck مقدار C برای کلاس k است. ایده کلی این است که جریمهی اشتباه در طبقهبندی کلاسهای اقلیت را افزایش دهیم تا از "غلبه" کلاس اکثریت بر آنها جلوگیری شود.
در کتابخانه scikit-learn، هنگام استفاده از SVC، میتوانیم مقادیر Ck را بهصورت خودکار با تنظیم class_weight="balanced" مشخص کنیم. آرگومان balanced بهصورت خودکار کلاسها را وزندهی میکند بهگونهای که:
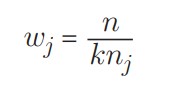
که در آن wj وزن کلاس j، n تعداد کل مشاهدات، nj تعداد مشاهدات در کلاس j، و k تعداد کل کلاسها است.

مطلبی دیگر از این انتشارات
فصل 20 -تنسورها با کتابخانه پایتورچ
مطلبی دیگر از این انتشارات
فصل 1. سازماندهی داده ها: موقعیت ، دامنه ، عمل و اعتبار
مطلبی دیگر از این انتشارات
فصل 21 - شبکههای عصبی