الگوریتم :Naive Bayes راهنمای کامل علاقمندان به علوم داده

منتشر شده در analyticsvidhya به تاریخ ۱۶ سپتامبر ۲۰۲۱
لینک منبع: Naive Bayes Algorithm: A Complete guide for Data Science Enthusiasts

مقدمه

در این مقاله، ما درباره شهود ریاضی پشت طبقه‌بندی کننده‌هایNaive Bayes بحث خواهیم کرد و همچنین نحوه پیاده‌سازی آن را بر روی پایتون خواهیم دید.

ساخت این مدل آسان است و عمدتا برای مجموعه داده‌های بزرگ استفاده می‌شود. این یک مدل یادگیری ماشینی احتمالاتی است که برای مسائل طبقه‌بندی استفاده می‌شود. هسته طبقه‌بندی‌کننده به قضیه Bayes با فرض استقلال در میان پیش‌بینی‌کننده‌ها بستگی دارد. این بدان معناست که تغییر ارزش یک ویژگی، مقدار ویژگی دیگر را تغییر نمی‌دهد.

چرا اسمش Naive است؟

این Naive نامیده می‌شود زیرا فرض بر این است که دو متغیر زمانی که ممکن است مستقل نباشند، مستقل هستند. در یک سناریوی دنیای واقعی، به ندرت موقعیتی وجود دارد که در آن ویژگی‌ها مستقل باشند.

به نظر می‌رسد الگوریتم ساده و در عین حال قدرتمندی باشد. اما چرا این قدر محبوب است؟

از آنجا که این یک رویکرد احتمالی است، پیش‌بینی‌ها را می‌توان به سرعت انجام داد. این روش را می‌توان هم برای مسائل طبقه‌بندی دودویی و هم برای مسائل طبقه‌بندی چند کلاسی به کار برد.

قبل از پرداختن عمیق‌تر به این موضوع، باید بدانیم که «احتمال شرطی» چیست، تئوری Bayes چیست و چگونه احتمال شرطی به ما در قضیه Bayes کمک می‌کند.

فهرست

۱. احتمال شرطی برای Naive Bayes

۲. قانون Bayes

۳. طبقه‌بندی کننده‌های Naive Bayes

۴. فرضیات Naive Bayes

۵. و Gaussian Naive Bayes

۶. اندنوت (End Notes)

احتمال شرطی برای Naive Bayes

احتمال شرطی به عنوان احتمال وقوع یک رویداد یا پیامد، براساس وقوع یک رویداد یا پیامد قبلی تعریف می‌شود. احتمال شرطی با ضرب احتمال رویداد قبلی با احتمال به‌روز شده رویداد بعدی یا شرطی محاسبه می‌شود.

بیایید درک این تعریف را با مثال شروع کنیم.

فرض کنید من از شما می‌خواهم که یک کارت را از روی عرشه انتخاب کنید و احتمال بدست آوردن شاه را با توجه به اینکه کارت گشنیز است، بیابید.

دقت کنید که من در اینجا شرایطی را ذکر کرده‌ام که کارت گشنیز باشد.

حال با محاسبه، احتمال اینکه مخرج من ۵۲ نخواهد بود، به جای آن، ۱۳ خواهد بود زیرا تعداد کل کارت‌های گشنیز ۱۳ است.

از آنجایی که ما تنها یک شاه در گشنیزها داریم، احتمال به دست آوردن شاه با توجه به این که کارت گشنیز است 13/۱ = ۰.۰۷۷ خواهد بود.

بیایید یک مثال دیگر بزنیم،

یک آزمایش تصادفی از بالا انداختن ۲ سکه را در نظر بگیرید. فضای نمونه در اینجا به صورت زیر خواهد بود:

S = { HH، HT، TH، TT }

اگر از فرد خواسته شود که احتمال گرفتن خط را پیدا کند، پاسخ او ۴/3 = ۰.۷۵ خواهد بود.

حال فرض کنید همین آزمایش توسط شخص دیگری انجام می‌شود اما اکنون ما به او این شرط را می‌دهیم که هر دو سکه شیر باشند. این بدان معنی است که اگر رویداد A: «هر دو سکه باید شیر باشند»، آنگاه پیامدهای اولیه { HT، TH، TT } نمی‌توانست اتفاق بیفتد. بنابراین در این وضعیت، احتمال گرفتن شیر بر روی هر دو سکه برابر ۴/۱ = ۰.۲۵ خواهد بود.

از مثال‌های بالا، مشاهده می‌کنیم که اگر برخی از اطلاعات اضافی به ما داده شود، احتمال ممکن است تغییر کند. این دقیقا همان موردی است که هنگام ساخت هر مدل یادگیری ماشینی وجود دارد، ما باید خروجی را با توجه به برخی ویژگی‌ها پیدا کنیم.

از لحاظ ریاضی، احتمال شرطی رویداد A که رویدادB پیش از این اتفاق‌افتاده است به صورت زیر است:

قانون Bayes

اکنون ما آماده‌ایم تا یکی از مفیدترین نتایج در احتمال شرطی را بیان کنیم: قانون .Bayes

تئوری Bayes که توسط توماس بیز، یک ریاضیدان انگلیسی، در سال ۱۷۶۳ ارائه شد، ابزاری را برای محاسبه احتمال یک رویداد با برخی اطلاعات فراهم می‌کند.

تئوری Bayes ریاضی را می‌توان به صورت زیر بیان کرد:

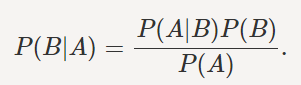
اساسا، ما در حال تلاش برای یافتن احتمال رویداد A هستیم، رویدادB داده‌شده درست است.

در اینجا P(B) احتمال قبلی نامیده می‌شود که به معنی احتمال یک رویداد قبل از شواهد است. P(B|A) احتمال پسین نامیده می‌شود یعنی احتمال یک رویداد پس از مشاهده شواهد.

با توجه به مجموعه داده‌های ما، این فرمول می‌تواند به صورت زیر بازنویسی شود:

متغیر Y کلاس متغیر

متغیر Xبردار ویژگی وابسته (اندازه n)

تعریف «Naive Bayes»

قانون Bayes، فرمولی را برای احتمال Y با توجه به برخی از ویژگی‌های X به ما می‌دهد. در مسائل دنیای واقعی، ما به سختی موردی را می‌یابیم که در آن تنها یک ویژگی وجود داشته باشد.

هنگامی که ویژگی‌ها مستقل هستند، می‌توانیم قاعده Bayes را به آنچه کهNaive Bayes نامیده می‌شود تعمیم دهیم که فرض می‌کند ویژگی‌ها مستقل هستند به این معنی که تغییر ارزش یک ویژگی بر مقادیر متغیرهای دیگر تاثیر نمی‌گذارد و به همین دلیل است که ما این الگوریتم را «NAIVE» می‌نامیم.

استانداردهای ساده می‌توانند برای چیزهای مختلفی مانند تشخیص چهره، پیش‌بینی آب و هوا، تشخیص پزشکی، طبقه‌بندی اخبار، تجزیه و تحلیل احساسات و خیلی چیزهای دیگر مورد استفاده قرار گیرند.

هنگامی که چندین متغیر X وجود دارند، با فرض این کهX مستقل است، آن را ساده می‌کنیم، بنابراین

برای n تعداد X، فرمول Naive Bayes می‌شود:

که می‌توان آن را به صورت زیر بیان کرد:

چون مخرج در اینجا ثابت است پس می‌توانیم آن را حذف کنیم. انتخاب شما است که می‌خواهید آن را حذف کنید یا خیر. حذف مخرج به شما در صرفه‌جویی در وقت و محاسبات کمک خواهد کرد.

این فرمول را می‌توان به صورت زیر نیز در نظر گرفت:

فرمول‌های زیادی در اینجا ذکر شده‌اند اما نگران نباشید ما سعی خواهیم کرد همه اینها را با کمک یک مثال درک کنیم.

مثال Naive Bayes

بیایید یک مجموعه داده بگیریم تا پیش‌بینی کنیم که آیا می‌توانیم یک حیوان را اهلی کنیم یا خیر.

فرضیات Naive Bayes

همه متغیرها مستقل هستند. اگر حیوان سگ باشد به این معنی نیست که اندازه متوسط خواهد بود

همه پیشگوها تاثیر یکسانی بر نتیجه دارند. به این معنی که سگ بودن حیوان در تصمیم‌گیری برای این که آیا می‌توانیم او را اهلی کنیم یا خیر، اهمیت بیشتری ندارد. تمام ویژگی‌ها اهمیت یکسانی دارند.

ما باید سعی کنیم که فرمول Naive Bayes را بر روی مجموعه داده‌های بالا اعمال کنیم، با این حال قبل از آن، ما باید برخی از پیش محاسبات را بر روی مجموعه داده‌های خود انجام دهیم.

ما باید P(xi|yj) را برای هرxi درX و هرyj درY پیدا کنیم. تمام این محاسبات در زیر نشان‌داده شده‌اند:

همچنین به احتمالات (P(y)) نیاز داریم، که در جدول زیر محاسبه شده‌اند. به عنوان مثال، P(حیوانات خانگی=(NO= ۱۴/۶.

حال اگر ما داده‌های آزمون خود را ارسال می‌کنیم، فرض آزمون = (گاو، متوسط، سیاه)

احتمال اهلی کردن یک حیوان:

و احتمال اهلی نکردن یک حیوان:

ما می دانیم که ) P بله|آزمایش) P + (نه|آزمایش) =1.

بنابراین، ما نتیجه را نرمال خواهیم کرد:

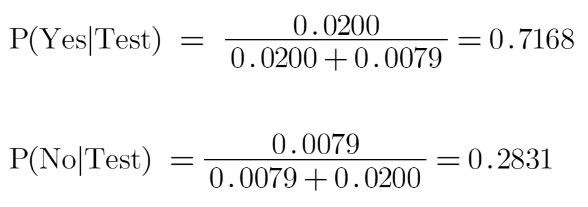
ما در اینجا می‌بینیم که P (بله|آزمایش) P < (نه|آزمایش)، بنابراین پیش‌بینی اینکه بتوانیم این حیوان را اهلی کنیم «بله» است.

حالت Gaussian Naive Bayes

تاکنون، ما در مورد چگونگی پیش‌بینی احتمالات در صورتی که پیش‌بینی‌کننده مقادیر گسسته را در نظر بگیرد، بحث کرده‌ایم. اما اگر پیوسته باشند چه؟ برای این کار، ما باید فرضیات بیشتری را در مورد توزیع هر ویژگی در نظر بگیریم. دسته‌بندی کننده‌های مختلف Naive Bayes عمدتا با فرضیاتی که در رابطه با توزیع P (xi| y) ایجاد می‌کنند، تفاوت دارند. در اینجا ما در مورد Gaussian Naive Bayes بحث خواهیم کرد.

حالت Gaussian Naive Bayes زمانی مورد استفاده قرار می‌گیرد که فرض کنیم همه متغیرهای پیوسته مربوط به هر ویژگی با توجه به توزیعGaussian توزیع شده‌اند. توزیع Gaussian نیز توزیع نرمال نامیده می‌شود.

در اینجا احتمال شرطی تغییر می‌کند زیرا ما در حال حاضر مقادیر متفاوتی داریم. همچنین تابع چگالی احتمال (PDF) یک توزیع نرمال به صورت زیر است:

اگر داده‌های ما پیوسته باشند، می‌توانیم از این فرمول برای محاسبه احتمال احتمالات استفاده کنیم.

کلام آخر

الگوریتم‌های Naive Bayes اغلب در تشخیص چهره، پیش‌بینی آب و هوا، تشخیص پزشکی، طبقه‌بندی اخبار، تجزیه و تحلیل احساسات و غیره استفاده می‌شوند. در این مقاله، ما شهود ریاضی پشت این الگوریتم را یاد گرفتیم. شما اولین قدم خود را برای تسلط بر این الگوریتم برداشته‌اید و از اینجا تمام چیزی که نیاز دارید تمرین است.

آیا این مقاله را مفید می‌دانید؟ لطفا نظرات/افکار خود را در بخش نظرات به اشتراک بگذارید.

درباره نویسنده

من در حال حاضر دانشجوی دوره کارشناسی رشته آمار هستم و علاقه زیادی به رشته علم داده، یادگیری ماشینی و هوش مصنوعی دارم. من از وارد شدن به داده‌ها برای کشف روندها و دیگر دیدگاه‌های ارزشمند در مورد داده‌ها لذت می‌برم. من دائما یاد می‌گیرم و انگیزه پیدا می‌کنم تا چیزهای جدید را امتحان کنم.

این متن با استفاده از ربات مترجم مقالات هوش مصنوعی ترجمه شده و به صورت محدود مورد بازبینی انسانی قرار گرفته است.در نتیجه می‌تواند دارای برخی اشکالات ترجمه باشد.

مقالات لینک‌شده در این متن می‌توانند به صورت رایگان با استفاده از مقاله‌خوان ترجمیار به فارسی مطالعه شوند.