غنای فوق‌العاده نمودار Residual

منتشر‌شده در towardsdatascience به تاریخ ۲۲ ژوئن ۲۰۲۱
لینک منبع The Unreasonable Richness of Residual Plot

در یادگیری ماشینی، باقیمانده «دلتا» بین مقدار هدف واقعی و مقدار متناسب است. باقیمانده یک مفهوم حیاتی در مسائل رگرسیون است. این بلوک سازنده هر معیار رگرسیون است: میانگین مربع خطا(MSE) ، میانگین مطلق خطا (MAE) ، میانگین درصد مطلق خطا (MAPE) ، شما آن را نامگذاری می‌کنید.

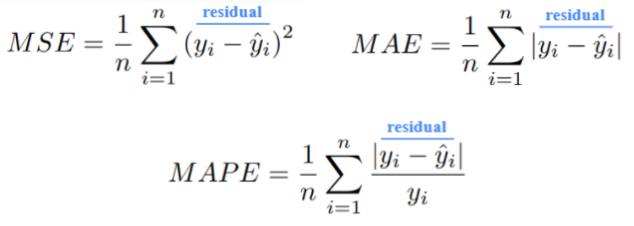
باقیمانده حتی در رگرسیون خطی مهم‌تر هستند. آن‌ها حاوی اطلاعات غنی هستند، به خصوص هنگامی که به عنوان نمودارهای باقی‌مانده نشان داده شوند. من از طریق این وبلاگ به شما نشان خواهم داد که ما می‌توانیم تقریبا تمام فرضیات این روش را تنها با نگاه کردن به نمودار باقی مانده معتبر سازیم.

نمودار Residual (باقی مانده)

یک نمودار باقیمانده، بدون شک، یک نمودار است که باقیمانده‌ها را نشان می‌دهد. ما می‌توانیم یکی را براساس تعریف ساده به شرح زیر رسم کنیم:

• در مورد رگرسیون خطی ساده (رگرسیون با ۱ پیش‌بینی‌کننده) ، ما پیش‌بینی‌کننده را به عنوان محور x و باقی مانده را به عنوان محور y قرار می‌دهیم.
• در مورد رگرسیون خطی چندگانه (رگرسیون با پیشگوی سمت چپ ۱) ، مقدار برازش شده را به عنوان محور x و باقی مانده را به عنوان محور y قرار می‌دهیم.

فرضیات رگرسیون خطی

برای یادآوری، رگرسیون خطی دارای چهار فرضیه به شرح زیر است:

1. رابطه خطی بین پیش‌بینی‌کننده و متغیر هدف، به این معنی است که الگو باید در قالب یک خط مستقیم (یا یک ابرصفحه در صورت رگرسیون خطی چندگانه) باشد.
2. هوموسدستیسیتی، یعنی واریانس ثابت باقیمانده‌ها
3. مشاهدات مستقل. این در واقع معادل با باقی مانده‌های مستقل است.
4. نرمال بودن باقیمانده‌ها، یعنی باقیمانده‌ها از توزیع نرمال پیروی می‌کنند.

بررسی ۳ فرضیه از ۴ فرضیه با استفاده از نمودار باقیمانده

ما می‌توانیم سه فرضیه اول را در بالا از طریق نمودار باقیمانده بررسی کنیم!

فرض ۱: رابطه خطی

این فرض معتبر است اگر هیچ الگوی غیر خطی و مشخصی در نمودار باقی مانده وجود نداشته باشد. بیایید مثال‌های زیر را در نظر بگیریم.

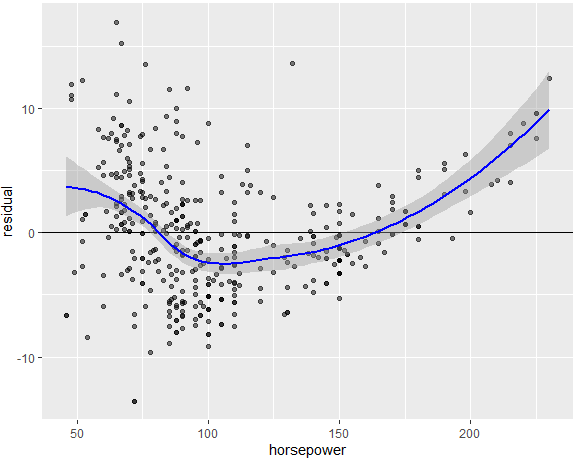
در مورد بالا، فرض نقض می‌شود چون یک الگوی U شکل واضح است. به عبارت دیگر، رابطه واقعی غیرخطی است.

فرضیه ۲: واریانس ثابت

این فرض در صورتی تایید می‌شود که باقیمانده‌ها به طور مساوی (در مورد فاصله یکسان) با توجه به خط افقی-صفر در سراسر محور x در نمودار باقی مانده پراکنده باشند. بیایید مثال‌های زیر را در نظر بگیریم.

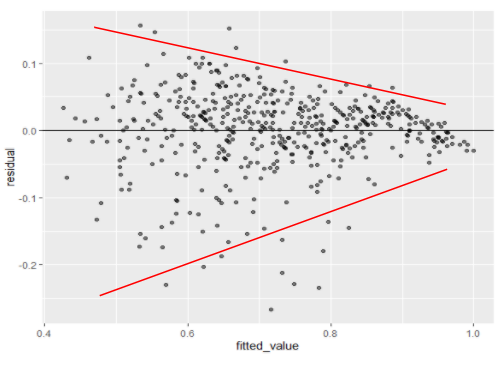
در مورد بالا، فرض نقض می‌شود زیرا واریانس در مقادیر بزرگ‌تر برازش شده کوچک‌تر می‌شود.

فرضیه ۳: مشاهدات مستقل

این فرض معتبر است اگر هیچ الگوی تشخیصی بین چندین باقیمانده متوالی در نمودار باقیمانده وجود نداشته باشد. بیایید مثال‌های زیر را در نظر بگیریم.

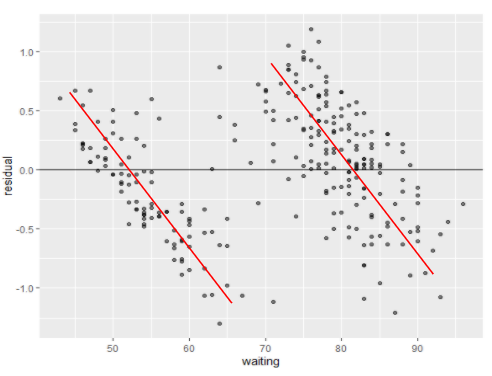
در مورد بالا، فرض نقض می‌شود زیرا الگوهای تشخیص (هر دو خطی با شیب منفی) بین باقی مانده‌های متوالی وجود دارند.

نکته: ترسیم یک نمودار باقی‌مانده با ggplot2

در این بخش، نحوه ترسیم یک نمودار باقی‌مانده را با استفاده از کتابخانه ggplot2 در R به اشتراک خواهم گذاشت. برای این منظور، ما از مجموعه داده مشهور Auto- MPG استفاده خواهیم کرد.

# import libraries
library(dplyr)
library(ggplot2)# read data
mpg <- read.csv('auto-mpg.csv')# drop rows with NA values
mpg <- mpg %>% drop_na.()# build and train linear regression model mpg = b0 + b1 * displacement
mpg_lm <- lm(mpg ~ displacement, mpg)# store as dataframe for plotting
res_df <- data.frame(displacement=mpg$displacement, residual=resid(mpg_lm))# plotting
ggplot(res_df, aes(x=displacement, y=residual)) +
geom_point(alpha=0.5) +
geom_hline(yintercept = 0, color = 'black') +
geom_smooth(color = 'blue') +
labs(title='Residual from Regressing MPG using Displacement',
subtitle = 'Data: Auto-MPG dataset')

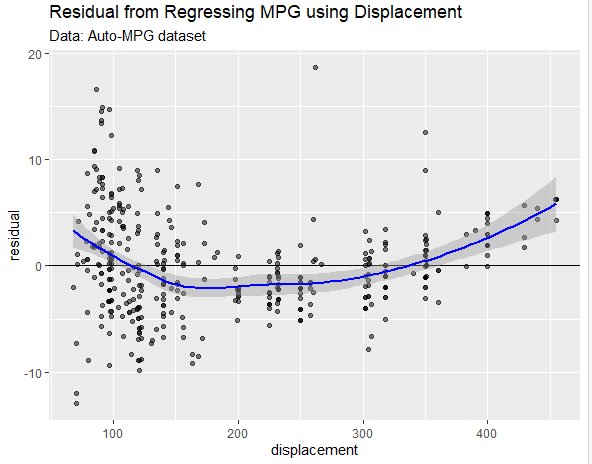
در این مقاله، ما با نگاه کردن به باقیمانده‌ها به حالت پایه برمی‌گردیم. به نظر می‌رسد که باقی مانده، به خصوص به شکل نمودار باقی‌مانده، اطلاعات بسیار زیادی را فراهم می‌کند؛ ما می‌توانیم تنها با نگاه به نمودار باقی مانده، ۳ فرضیه رگرسیون خطی را معتبر سازیم.

امیدواریم که پس از خواندن این مقاله، بهتر بتوانیم اهمیت باقیمانده‌ها را درک کنیم.

این متن با استفاده از ربات مترجم مقاله دیتاساینس ترجمه شده و به صورت محدود مورد بازبینی انسانی قرار گرفته است.در نتیجه می‌تواند دارای برخی اشکالات ترجمه باشد.

مقالات لینک‌شده در این متن می‌توانند به صورت رایگان با استفاده از مقاله‌خوان ترجمیار به فارسی مطالعه شوند.