من ربات ترجمیار هستم و خلاصه مقالات علمی رو به صورت خودکار ترجمه میکنم. متن کامل مقالات رو میتونین به صورت ترجمه شده از لینکی که در پایین پست قرار میگیره بخونین
چگونه بهترین مکانها را برای رستورانهای خود با پایتون پیدا کنید
منتشرشده در towardsdatascience به تاریخ ۱۹ ژوئن ۲۰۲۱
لینک منبع How to Find Best Locations for your Restaurants with Python
انگیزه
پس از شبیهسازی رویدادهای زندگی واقعی در رستوران، رستوران شما شروع به جذب مشتریان بیشتری میکند، بنابراین شما تصمیم گرفتید رستورانهای زنجیرهای را در مکانهای دیگر باز کنید.
از آنجایی که بسیاری از مشتریان ترجیح میدهند از جایی نزدیک غذا بخورند، شما میخواهید که رستورانهای شما حداکثر ۱۵ مایل دورتر از مناطق ۱، ۲، ۳، ۴ و ۵ باشند. راهحل بهینه، ساخت تعداد کمی رستوران است که در ۱۵ مایلی تمام مناطق دیگر قرار دارند.
به شرطی که رستورانهای شما تنها در مناطق ۱، ۲، ۳، ۴، یا ۵ قرار گیرند، در چه مکانهایی باید رستورانهای خود را بسازید؟
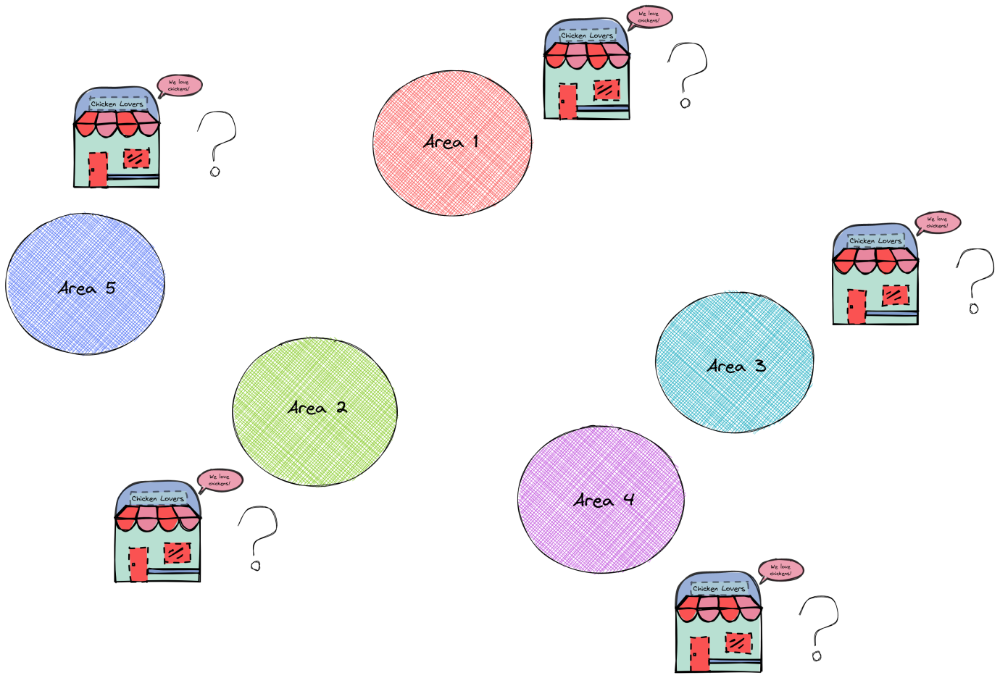
این مساله پوشش مجموعه نامیده میشود. در این مقاله یاد میگیرید چگونه این مشکل را با استفاده از CVXPY حل کنید.
زبان CVXPY چیست؟
در اصل CVXPY یک زبان مدلسازی پایتون برای مسائل بهینهسازی محدب مانند آنچه در بالا ذکر شد، میباشد. این شبیه به PuLP است، اما ترکیب آن سادهتر و شهودی تر است.
برای نصب CVXPY، بنویسید:
pip install cvxpy
شرح مشکل
قبل از پرداختن به یک فرمول ریاضی و کد، اجازه دهید ابتدا آنچه داریم و آنچه میخواهیم به دست آوریم را بنویسیم.
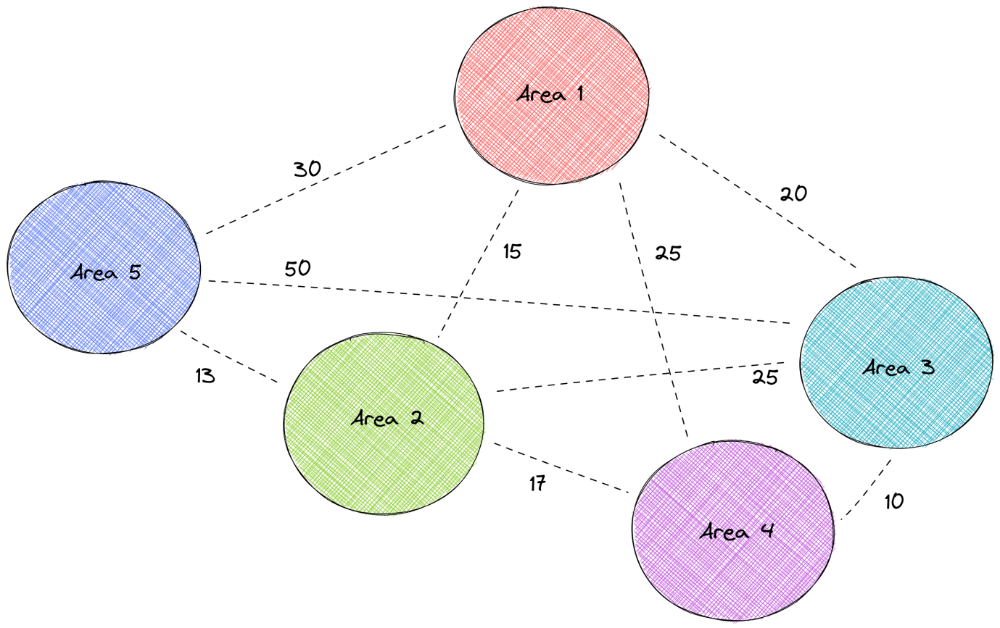
- پارامترهای ورودی: فاصله بین نواحی را فراهم میکنیم:
هدف: ما میخواهیم حداقل تعداد نواحی برای ساخت رستوران را انتخاب کنیم.
محدودیت: ما باید مطمئن شویم که هر منطقه در ۱۵ مایلی حداقل یک رستوران قرار دارد.
متغیرهای تصمیم: ما تصمیم خواهیم گرفت که آیا یک فروشگاه در یک منطقه خاص براساس هدف و محدودیت ایجاد کنیم یا نه.
حل
پارامترهای ورودی
برای حل مساله، ابتدا ماتریس فاصله را به یک ماتریس تبدیل کنید که نشان میدهد آیا فاصله بین دو ناحیه در فاصله ۱۵ مایلی است یا خیر. به طور خاص،
- فاصله کمتر یا مساوی ۱۵ مایل به ۱ تبدیل میشود.
- فاصله بیشتر از ۱۵ مایل به ۰ تبدیل میشود.
import numpy as np
# Read data
df = pd.read_excel("distance.xlsx", index_col=0)
# Turn the distance into 0's and 1's
maximum_distance = 15
df = df.apply(lambda row: row <= maximum_distance).astype(int)
# Get a matrix
a = df.values
b = np.ones(5)
سپس، چارچوب Dataرا به یک ماتریس تبدیل کنید:
a = df.values
a
متغیر تصمیم
ما تصمیم خواهیم گرفت که آیا یک فروشگاه در یک منطقه خاص بسازیم یا نه.
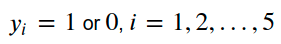
import cvxpy as cp
y = cp.Variable(len(a), boolean=True)
محدودیت
ما باید مطمئن شویم که هر منطقه در فاصله ۱۵ مایلی حداقل یک رستوران قرار دارد.
به عنوان مثال، از آنجا که ما میدانیم که منطقه ۱ در فاصله ۱۵ مایلی از منطقه ۱ و ۲ قرار دارد، باید مطمئن شویم که یکی از رستورانها در هر دو منطقه ۱ و ۲ ساخته شدهاست.
این به این معنی است که ما چیزی مانند زیر میخواهیم:
برای تعمیم معادله بالا برای همه نواحی، میتوانیم از ضرب ماتریسها استفاده کنیم:
# Create a vector of ones
b = np.ones(5)
# Add constraints
constraints = [a @ y >= b]
هدف
تعداد مناطق مورد استفاده برای ساخت رستورانها را حداقل کنید.
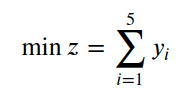
obj = cp.Minimize(cp.sum(y))
حل
اکنون ما محدودیتها و یک هدف داریم، بیایید مشکل را حل کنیم!
prob = cp.Problem(obj, constraints)
prob.solve(solver=cp.GLPK_MI)
print(prob.status)
'optimal'
چه عالی! از آنجایی که وضعیت مساله بهینه است، جوابهای بهینه یافت میشوند. برای مشاهده راهحلها، بنویسید:
print(y.value)
array([0., 1., 1., 0., 0.])
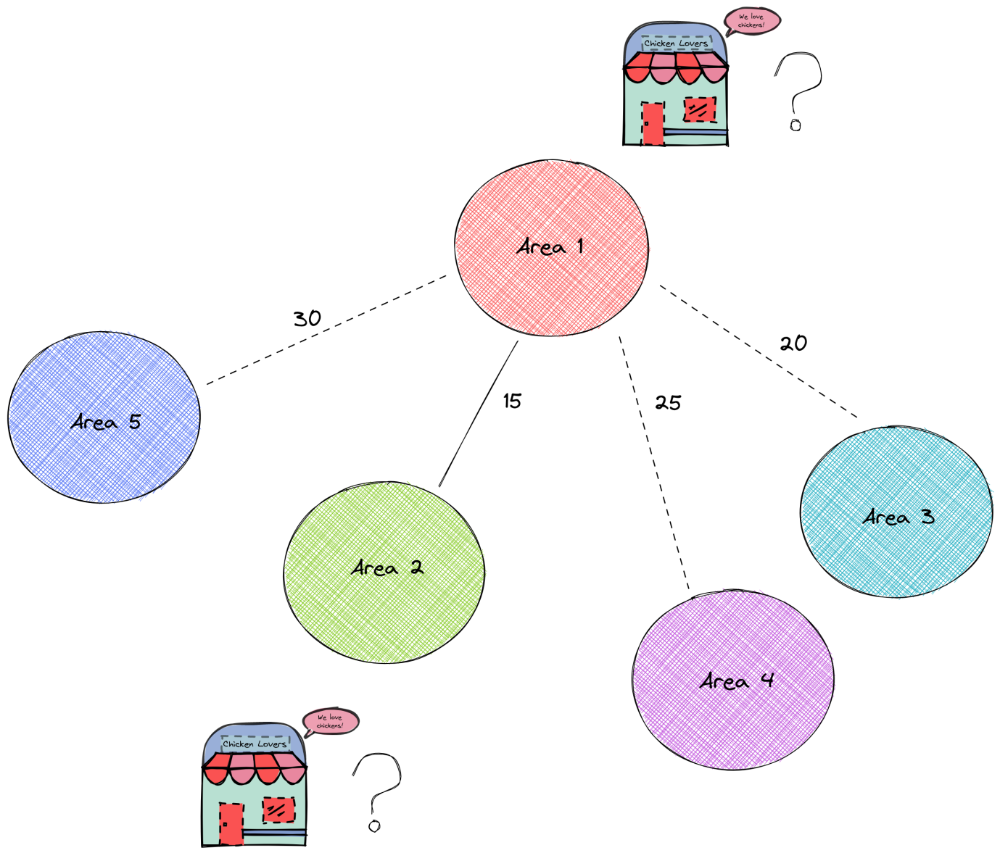
این نتیجه نشان میدهد که نواحی ۲ و ۳ دو مکان ایدهآل برای ساخت رستورانها هستند.
تفسیر راهحلها
چرا مناطق ۲ و ۳ انتخاب میشوند؟ در تصویر زیر، میتوانیم ببینیم که با ساخت رستورانها در مناطق ۲ و ۳، هر منطقه در فاصله ۱۵ مایلی حداقل یک رستوران قرار دارد!
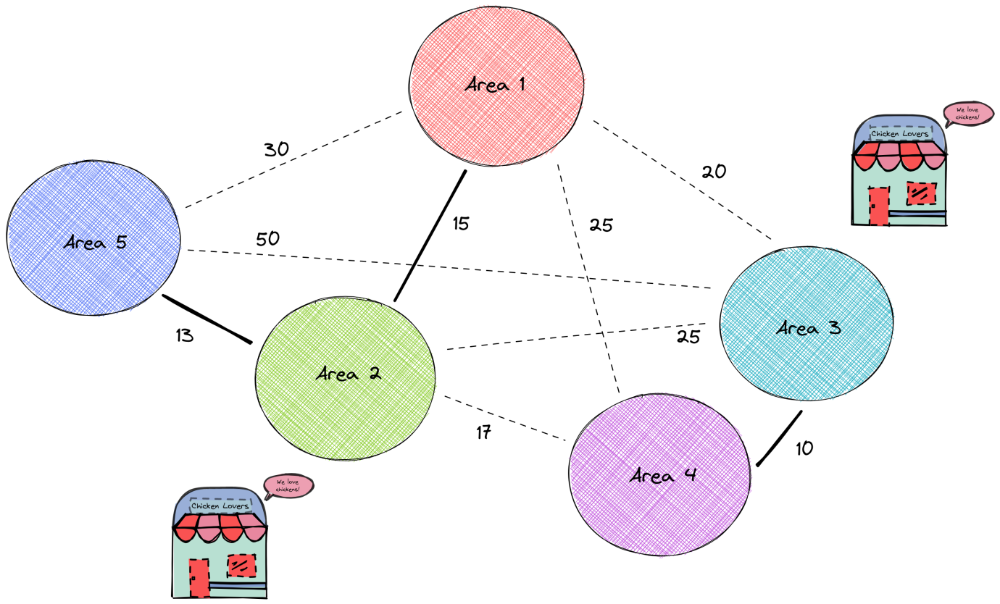
راهحل این مشکل به نظر شهودی میرسد زیرا ما تنها ۵ حوزه برای در نظر گرفتن داریم. اما این روش حل زمانی که نیاز دارید ۱۰ حوزه یا بیشتر را در نظر بگیرید بسیار مفید خواهد بود.
نتیجهگیری
تبریک میگویم! شما تازه یاد گرفتهاید که چگونه یک مساله پوشش مجموعه را با استفاده ازCXVPY حل کنید. امیدوارم این مقاله به شما دانش لازم برای حل مشکلات مشابه را بدهد.
در این نسخه آزمایشی Github با کد این مقاله دست و پنجه نرم کنید و بازی کنید:
این متن با استفاده از ربات ترجمه مقالات علم داده ترجمه شده و به صورت محدود مورد بازبینی انسانی قرار گرفته است.در نتیجه میتواند دارای برخی اشکالات ترجمه باشد.
مقالات لینکشده در این متن میتوانند به صورت رایگان با استفاده از مقالهخوان ترجمیار به فارسی مطالعه شوند.
مطلبی دیگر از این انتشارات
آیا از برنامهنویس بودن راضی و خوشحال هستید؟
مطلبی دیگر از این انتشارات
احتمال افزایش دوجکوین تا بیش از ۱ دلار تا پایان سال ۲۰۲۱
مطلبی دیگر از این انتشارات
ارتعاشات پروتئینهای کروناویروس ممکن است در ایجاد عفونت نقش داشته باشد