اهداف مقاله
افراد شاغل در یادگیری ماشین بیشتر زمان خود را صرف ارزیابی، تمیز کردن داده ها، و تغییر شکل دادن داده ها هستند تا ساخت مدل ها. داده بسیار با اهمیت است که این مقاله تمامی سه واحد زیر را به این موضوع اختصاص میدهد:
این بخش بر روی داده های عددی تمرکز میکند، به عبارت دیگه اعداد صحیح و یا اعشاری. این داده ها قابل جمع کردن، شمارش، مرتب کردن و غیره هستند. در بخش بعدی بر روی داده های طبقه بندی شده تمرکز میکنیم که شامل اعدادی هستند که مانند دسته ها رفتار میکنند. در بخش سوم بر روی اینکه چطور میتوانیم داده هایمان را اماده کنیم تا نتایج با کیفیت بالا بدست آوریم در موقع آموزش مدل و چگونگی ارزیابی مدل تمرکز میکنیم.
امثال داده های عددی:
در مقابل، کدپستی در امریکا، با وجود ۵ یا ۹ رقمی بودن، همانند اعداد رفتار نمیکند چرا که روابط ریاضی بر روی آنها اعمال نمیشود. کد پستی ۴۰۰۰۴ در کنتاکی دو برابر از لحاظ تعداد در مقایسه با کد پستی ۲۰۰۰۲ در واشنگتن دی سی نیست. این ارقام دسته بندی ها و نواحی جغرافیایی را نشان میدهند.
فرض کنید یک مجموعه داده شامل ۵ ستون است ولی فقط ۲ تا از ستون ها به عنوان ویژگی در مدل هستند. مدل یک آرایه ای از اعداد اعشاری به نام بردار ویژگی را هزم میکند. یک بردار ویژگی یک نمونه را میسازد.
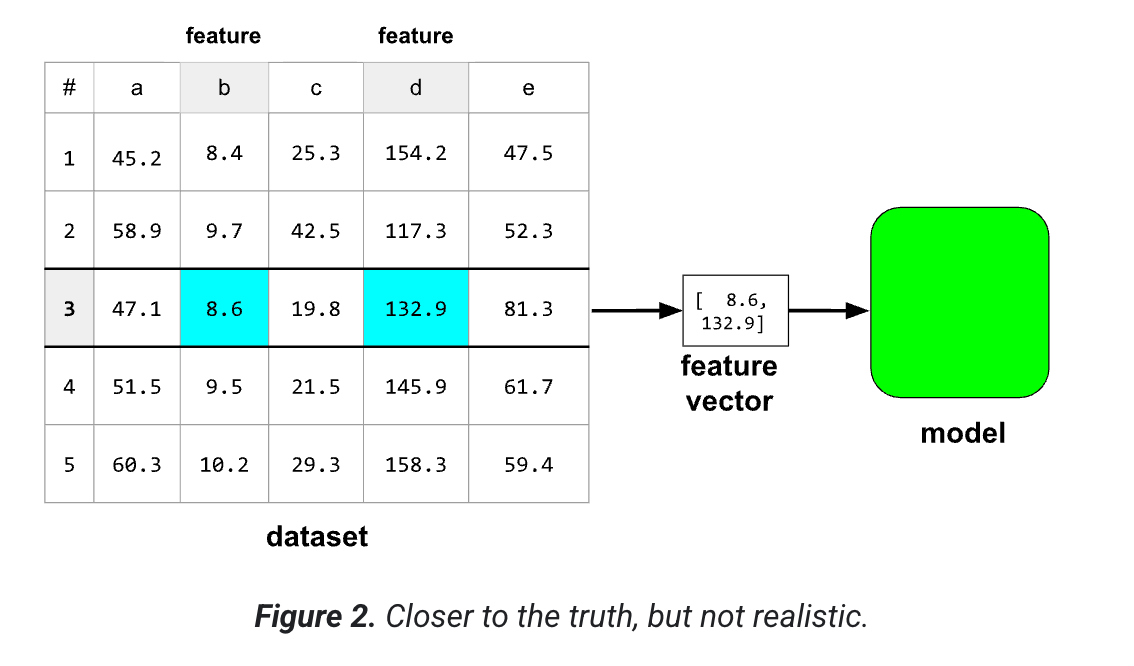
بردارهای ویژگی به ندرت از مقادیر خام در مجموعه داده استفاده میکنند. معمولا مقادیر باید برای مدل بهینه شوند. بنابراین یک ویژگی واقع بینانه تر ممکن است به این شکل باشد:
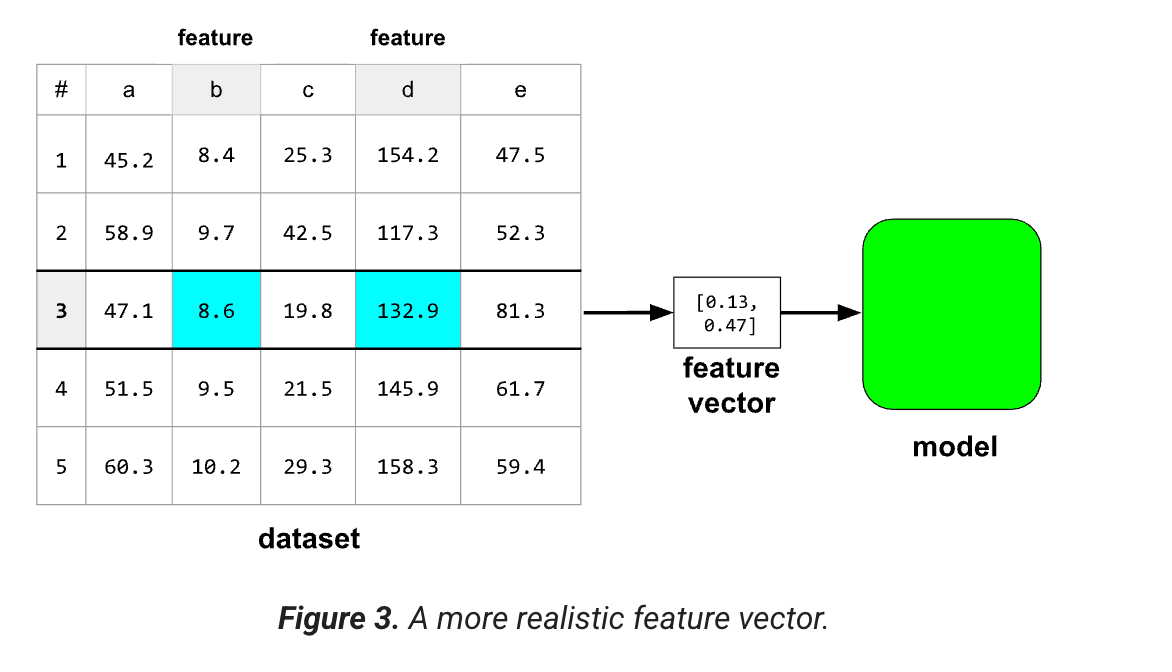
ولی آیا یک مدل با مقادیر واقعی در یک مجموعه داده پیش بینی های بهتری انجام نمیدهد؟ جواب خیر است.
باید بهترین راه برای بهتر ارائه داده ویژگی ها برای روند آموزش مدل را پیدا کنید. به این پروسه مهندسی ویژگی گفته میشود و معمولا قسمت حیاتی یادگیری ماشین است. متداول ترین تکنیک های مهندسی ویژگی عبارتند از:
قبل از ساخت بردار های ویژگی توصیه میکنیم که داده های عددی را در دو طریق مطالعه کنید:
گراف ها میتوانند کمک کنند تا نمونه های غیر معمول یا الگو های مخفی در داده ها را بیابیم. بنابراین قبل از اینکه خیلی وارد تجزیه و تحلیل شویم نگاهی کنیم به داده ها به صورت تصویری مانند رسم نمودار یا هیستوگرام.
علاوه بر بررسی تصویری توصیه میشود که ویژگی ها و برچسب ها به صورت ریاضیاتی ارزیابی شوند. موارد اماری ابتدایی همانند:
یک مورد پرت مقداری دور از سایر مقادیر در یک ویژگی یا برچسب میباشد. موارد پرت اغلب باعث بروز مشکلات در یادگیری مدل میشوند بنابرین پیدا کردنشان بسیار با اهمیت است.
وقتی که دلتا بین صدک صفرم و ۲۵ام بسیار تفاوت دارند با صدک بین ۷۵ ام و ۱۰۰ ام، احتمالا مجموعه داده شامل موارد پرت میباشد.
پرت ها می توانند در هر یک از دسته های زیر قرار گیرند:
- پرت ناشی از اشتباه است. به عنوان مثال، شاید یک آزمایشگر به اشتباه یک صفر اضافی را وارد کرده است، یا شاید ابزاری که داده ها را جمع آوری می کند دچار مشکل شده است. شما به طور کلی نمونه های حاوی خطاهای پرت را حذف خواهید کرد.
- نقطه پرت یک نقطه داده مشروع است، نه یک اشتباه. در این صورت، آیا مدل آموزشدیده شما در نهایت نیاز به استنباط پیشبینیهای خوب در مورد این نقاط پرت دارد؟
اگر بله، این موارد پرت را در مجموعه آموزشی خود نگه دارید. به هر حال، نقاط پرت در برخی ویژگیها، گاهی اوقات منعکس کننده موارد پرت در برچسب هستند، بنابراین نقاط پرت در واقع میتوانند به مدل شما کمک کنند تا پیشبینی بهتری داشته باشد. مراقب باشید، پرت های شدید همچنان می تواند به مدل شما آسیب برساند.
اگر نه، نقاط پرت را حذف کنید یا از تکنیکهای مهندسی ویژگیهای تهاجمیتر، مانند بریدن استفاده کنید.
پس از اینکه داده ها را از نظر آماری و بصیری بررسی کردیم باید داده ها را به شکلی تغییر شکل دهیم که به مدل کمک کند تا بهینه تر آموزش ببیند. برای مثل این دو ویژگی را در نظر بگیرید
این دو ویژگی میتوانند رنج های متفاوتی داشته باشند. نرمال سازی ممکن است ویژگی های x و y را به گونه ای تغییر دهد که رنج یکسانی داشته باشند. مثلا بین صفر و یک.
نرمال سازی کمک میکند تا
دو ویژگی زیر را در نظر بگیرید:
کمترین مقدار ویژگی A 0.5- و بیشترین مقدار 0.5+ است.
کمترین مقدار ویژگی B -5.0 و بالاترین +5.0 است.
ویژگی A و ویژگی B دهانه های نسبتاً باریکی دارند. با این حال، دهانه ویژگی B 10 برابر بیشتر از دهانه ویژگی A است. بنابراین:
در شروع آموزش، مدل فرض میکند که ویژگی B ده برابر «مهمتر» از ویژگی A است.
آموزش بیش از آنچه باید طول بکشد.
مدل حاصل ممکن است کمتر از حد بهینه باشد.
آسیب کلی ناشی از عادی نشدن نسبتاً کوچک خواهد بود. با این حال، ما همچنان توصیه می کنیم که ویژگی A و ویژگی B را در یک مقیاس، شاید -1.0 تا +1.0 عادی کنید.
اکنون دو ویژگی را با اختلاف دامنه بیشتر در نظر بگیرید:
کمترین مقدار ویژگی C -1 و بیشترین مقدار 1+ است.
کمترین مقدار ویژگی D 5000+ و بیشترین مقدار 1,000,000,000+ است.
اگر ویژگی C و ویژگی D را عادی نکنید، مدل شما احتمالاً کمتر از حد مطلوب خواهد بود. علاوه بر این، آموزش خیلی بیشتر طول می کشد تا همگرا شوند یا حتی نتوانند به طور کامل همگرا شوند!
این بخش سه روش عادی سازی رایج را پوشش می دهد:
مقیاس بندی خطی
مقیاس بندی Z-score
مقیاس بندی ورود به سیستم
این بخش علاوه بر این برش را پوشش می دهد. اگرچه یک تکنیک عادی سازی واقعی نیست، اما برش ویژگی های عددی سرکش را در محدوده هایی که مدل های بهتری تولید می کنند رام می کند.
مقیاسبندی خطی (که معمولاً کوتاهتر میشود) به معنای تبدیل مقادیر ممیز شناور از محدوده طبیعی آنها به یک محدوده استاندارد است - معمولاً 0 تا 1 یا -1 به +1.
مقیاس خطی انتخاب خوبی است زمانی که تمام شرایط زیر برآورده شود:
مرزهای پایین و بالای داده های شما در طول زمان تغییر چندانی نمی کند.
این ویژگی حاوی مقادیر کمی است یا اصلاً وجود ندارد، و آن نقاط پرت شدید نیستند.
این ویژگی تقریباً به طور یکنواخت در محدوده آن توزیع شده است. به این معنا که یک هیستوگرام تقریباً میله های یکنواخت را برای اکثر مقادیر نشان می دهد.
فرض کنید سن انسان یک ویژگی است. مقیاس بندی خطی یک تکنیک نرمال سازی خوب برای سن است زیرا:
کران پایین و بالایی تقریبی 0 تا 100 است.
سن شامل درصد نسبتا کمی از نقاط پرت است. فقط حدود 0.3 درصد از جمعیت بالای 100 سال هستند.
اگرچه سنین خاص تا حدودی بهتر از سایرین نمایش داده می شوند، یک مجموعه داده بزرگ باید شامل نمونه های کافی از همه سنین باشد.
فرض کنید مدل شما دارای ویژگی به نام net_worth است که دارایی خالص افراد مختلف را در خود جای داده است. آیا مقیاس خطی یک تکنیک عادی سازی خوب برای net_worth خواهد بود؟ چرا یا چرا نه؟
پاسخ: مقیاسبندی خطی انتخاب ضعیفی برای عادیسازی net_worth خواهد بود. این ویژگی حاوی مقادیر پرت بسیاری است و مقادیر به طور یکنواخت در محدوده اصلی آن توزیع نمی شوند. اکثر مردم در یک باند بسیار باریک از محدوده کلی فشرده می شوند.
عدد Z-score تعداد انحرافات استاندارد یک مقدار از میانگین است. به عنوان مثال، مقداری که 2 انحراف استاندارد بیشتر از میانگین است دارای امتیاز Z 2.0+ است. مقداری که 1.5 انحراف استاندارد کمتر از میانگین است دارای امتیاز Z -1.5 است.
امتیاز z-score زمانی که داده ها از توزیع نرمال یا توزیعی تا حدودی شبیه توزیع نرمال پیروی می کنند، انتخاب خوبی است.
توجه داشته باشید که برخی توزیعها ممکن است در بخش عمده دامنه خود نرمال باشند، اما همچنان شامل دادههای پرت شدید باشند. برای مثال، تقریباً همه نقاط در یک ویژگی net_worth ممکن است به خوبی در ۳ انحراف استاندارد قرار بگیرند، اما چند نمونه از این ویژگی میتوانند صدها انحراف استاندارد از میانگین فاصله داشته باشند. در این شرایط، میتوانید مقیاسبندی Z-score را با شکل دیگری از نرمالسازی (معمولاً حذف مقادیر اضافی) ترکیب کنید تا این وضعیت را مدیریت کنید.
درک خود را بررسی کنید فرض کنید مدل شما روی ویژگی به نام height که شامل قد بزرگسالان ده میلیون زن است، آموزش میبیند. آیا مقیاسبندی Z-score روش خوبی برای نرمالسازی height است؟ چرا؟
پاسخ: مقیاسبندی Z-score روش خوبی برای نرمالسازی height خواهد بود زیرا این ویژگی با توزیع نرمال مطابقت دارد. ده میلیون نمونه حاکی از تعداد زیادی داده پرت است - احتمالاً داده پرت کافی برای یادگیری الگوها توسط مدل روی نمرات Z بسیار بالا یا بسیار پایین است.مقیاسبندی لگاریتمی، لگاریتم مقدار خام را محاسبه میکند. در تئوری، لگاریتم میتواند هر پایه ای داشته باشد. در عمل، مقیاسبندی لگاریتمی معمولاً لگاریتم طبیعی (ln) را محاسبه میکند.
مقیاسبندی لگاریتمی زمانی مفید است که دادهها با توزیع قانون توانی مطابقت داشته باشند. به زبان ساده، توزیع قانون توانی به صورت زیر است: مقادیر پایین X، مقادیر بسیار بالایی از Y دارند. همانطور که مقادیر X افزایش مییابند، مقادیر Y به سرعت کاهش مییابند. در نتیجه، مقادیر بالای X، مقادیر بسیار پایینی از Y دارند. امتیازدهی فیلمها نمونه خوبی از توزیع قانون توانی است. در شکل زیر به موارد زیر توجه کنید: تعداد کمی از فیلمها امتیازهای کاربری زیادی دارند. (مقادیر پایین X، مقادیر بالای Y دارند.) اکثر فیلمها امتیازهای کاربری بسیار کمی دارند. (مقادیر بالای X، مقادیر پایین Y دارند.) مقیاسبندی لگاریتمی توزیع را تغییر میدهد که به آموزش مدلی که پیشبینیهای بهتری انجام میدهد، کمک میکند.
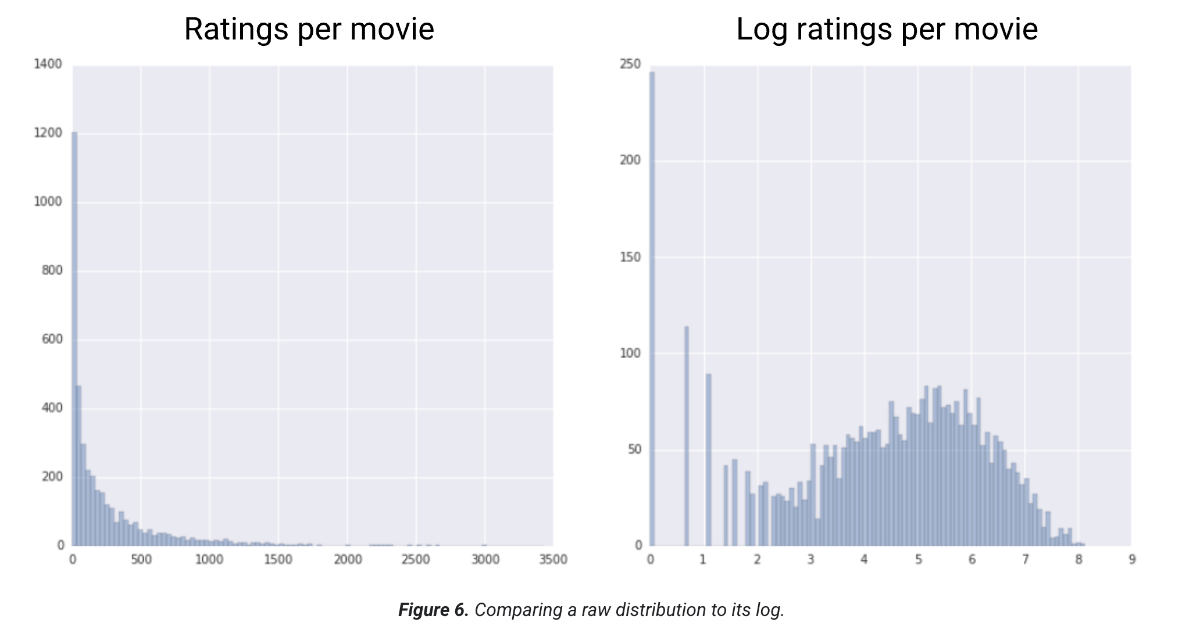
به عنوان مثال دوم، فروش کتاب با توزیع قانون توانی مطابقت دارد زیرا:
- اکثر کتابهای منتشر شده تعداد کمی نسخه میفروشند، شاید یکی دو صد نسخه.
- برخی از کتابها تعداد متوسطی نسخه میفروشند، در حد هزاران نسخه.
- فقط تعداد کمی از پرفروشترینها بیش از یک میلیون نسخه خواهند فروخت.
فرض کنید شما در حال آموزش یک مدل خطی برای یافتن رابطه، مثلاً بین جلد کتاب و فروش کتاب هستید. یک مدل خطی که روی مقادیر خام آموزش میبیند، باید چیزی در مورد جلد کتابهایی که یک میلیون نسخه میفروشند پیدا کند که ۱۰ هزار برابر قویتر از جلد کتابهایی باشد که فقط ۱۰۰ نسخه میفروشند. با این حال، مقیاسبندی لگاریتمی همه ارقام فروش، این کار را بسیار امکانپذیرتر میکند. به عنوان مثال، لگاریتم ۱۰۰ برابر است با:
~۴٫۶ = ln(۱۰۰)
در حالی که لگاریتم ۱,۰۰۰,۰۰۰ برابر است با:
~۱۳٫۸ = ln(۱,۰۰۰,۰۰۰)
بنابراین، لگاریتم ۱,۰۰۰,۰۰۰ فقط حدود سه برابر بزرگتر از لگاریتم ۱۰۰ است. احتمالاً میتوانید تصور کنید که جلد یک کتاب پرفروش حدود سه برابر قویتر (به نوعی) از جلد یک کتاب با فروش بسیار کم باشد.
حذف مقادیر اضافی تکنیکی برای به حداقل رساندن تأثیر دادههای پرت شدید است. به طور خلاصه، حذف مقادیر اضافی معمولاً مقدار دادههای پرت را به یک مقدار حداکثر خاص محدود (کاهش) میکند. حذف مقادیر اضافی ایده عجیبی است، اما در عین حال میتواند بسیار مؤثر باشد.
برای مثال، مجموعه دادهای را تصور کنید که شامل ویژگی به نام roomsPerPerson است که نشان دهنده تعداد اتاقها (کل اتاقها تقسیم بر تعداد ساکنان) برای خانههای مختلف است. نمودار زیر نشان میدهد که بیش از ۹۹ درصد از مقادیر ویژگی با توزیع نرمال مطابقت دارند (تقریباً، میانگین ۱.۸ و انحراف استاندارد ۰.۷). با این حال، این ویژگی شامل چند داده پرت است که برخی از آنها شدید هستند:
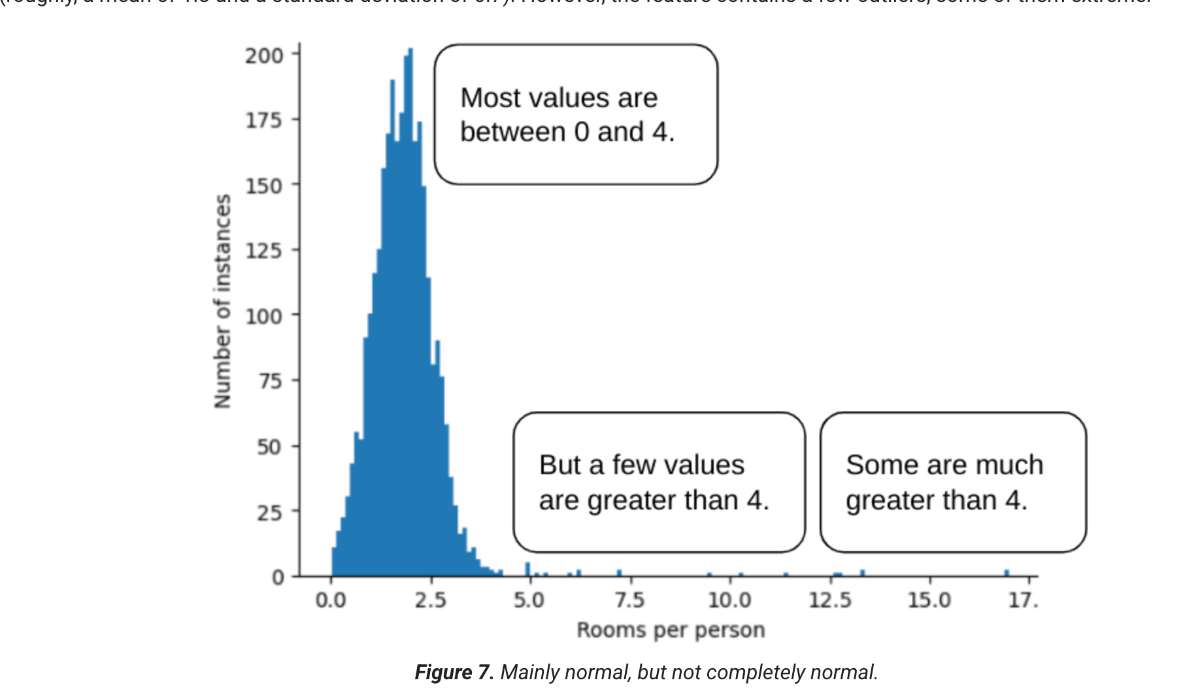
چگونه میتوانید تأثیر آن دادههای پرت شدید را به حداقل برسانید؟ خب، نمودار هیستوگرام نه یک توزیع یکنواخت، نه یک توزیع نرمال و نه یک توزیع قانون توانی است. اگر به سادگی مقدار حداکثر roomsPerPerson را در یک مقدار دلخواه، مثلاً ۴.۰،۱ محدود یا حذف کنید، چه؟
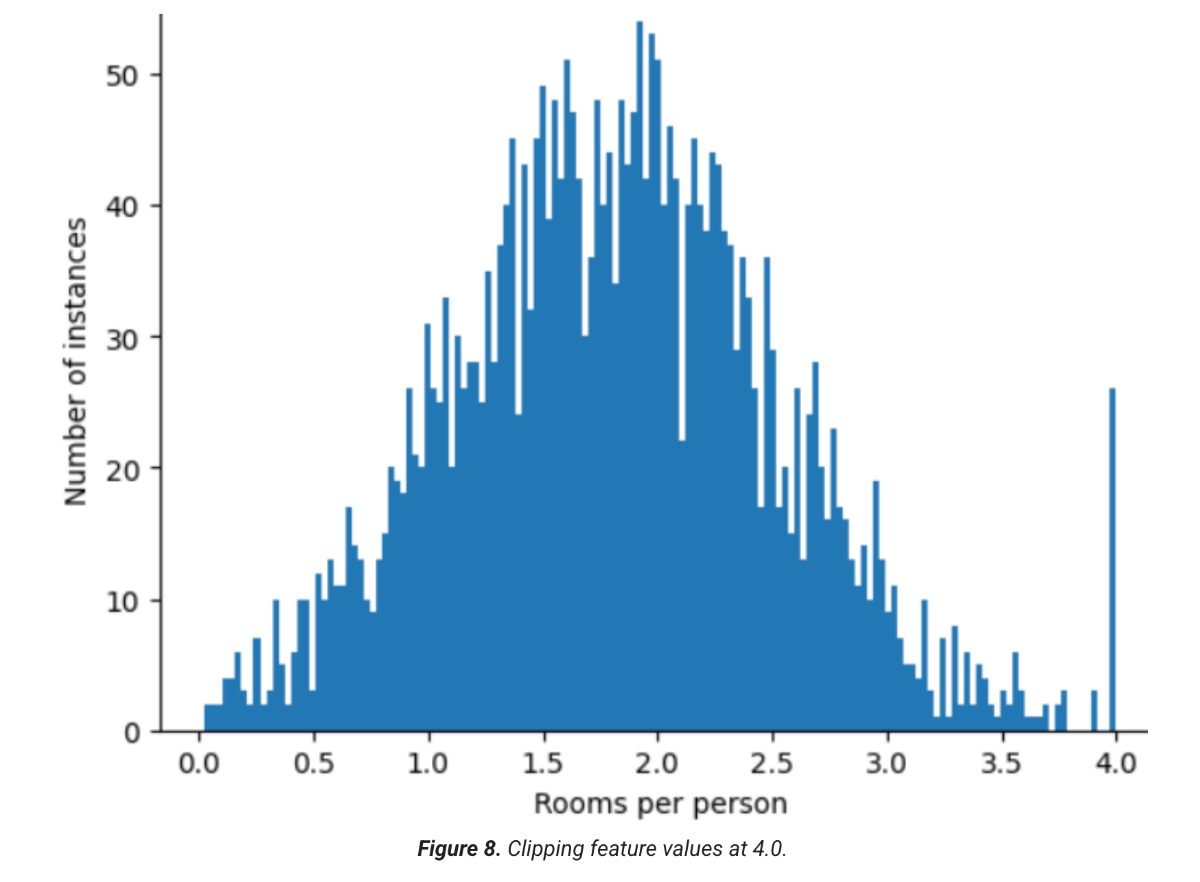
محدود کردن مقدار ویژگی به ۴.۰ به این معنا نیست که مدل شما همه مقادیر بزرگتر از ۴.۰ را نادیده میگیرد. بلکه به این معناست که همه مقادیری که بزرگتر از ۴.۰ بودند، اکنون ۴.۰ میشوند. این موضوع، تپه عجیب در ۴.۰ را توضیح میدهد. علیرغم این تپه، مجموعه ویژگی مقیاسشده اکنون مفیدتر از دادههای اصلی است.
صبر کنید! آیا واقعاً میتوانید هر مقدار پرت را به یک آستانه بالایی دلخواه کاهش دهید؟ هنگام آموزش یک مدل، بله.
همچنین میتوانید مقادیر را پس از اعمال اشکال دیگر نرمالسازی محدود کنید. برای مثال، فرض کنید از مقیاسدهی Z-score استفاده میکنید، اما چند داده پرت، مقادیر مطلقی بسیار بزرگتر از ۳ دارند. در این صورت، میتوانید:
محدود کردن، از بیش از حد نمایه شدن مدل شما روی دادههای بیاهمیت جلوگیری میکند. با این حال، برخی از دادههای پرت در واقع مهم هستند، بنابراین مقادیر را با دقت محدود کنید.
