منبع اصلی این پست، دوره NLP استنفورد (CS224N) از کانال یوتیوب Stanford Online است. لطفاً برای حفظ حقوق منتشر کننده اصلی، ویدیوهارو از منبع اصلی دنبال کنید. همچنین، در انتهای هر جلسه، به ویدیو مربوط به آن جلسه ارجاع داده شده است.

سعی کردم هرچیزی که از ویدیوها فهمیدم رو به صورت متن در بیارم و در این پلتفورم با بقیه به صورت کاملاً رایگان به اشتراک بذارم. کل ویدیوها 23 تاست که سعی میکنم ماهی حداکثر یک الی دو جلسه رو منتشر کنم. تا جایی که تونستم سعی کردم خوب و کامل بنویسم، اما اگر جایی ایرادی داشت، حتما تو کامنتها بهم بگید تا درستش کنم. لازم به ذکره که برای فهم بهتر مباحث این دوره، دونستن مفاهیم پایهای در یادگیری ماشین، جبر خطی و آمار و احتمال پیشنهاد میشه.
جنس این جلسه بیشتر ریاضی محور و تئوریه، البته مباحث غیر ریاضی هم داره. قراره در مورد شبکههای عصبی عمیق حرف بزنیم و بیایم دستی گرادیان حساب کنیم. شاید فکر کنید اصلاً نیازی به این همه دیتیل از ریاضیات نداریم و اصلاً چه نیازیه که این همه ریاضی بدونیم! ولی به نظر من اگه این مباحث مهم نبودن و نیاز به یادگیریشون نبود نمیومدن یک جلسه از این دوره رو به صورت خاص به این مباحث اختصاص بدن! اگه تا الان، همیشه از این مباحث فراری بودین، این بلاگ پست و این جلسه از دوره رو بعنوان یه فرصت جدید بهش نگاه کنید، شاید با دفعههای قبلی فرق داشت و خوشتون اومد!
قراره با یک تسک NLP ساده این جلسه رو شروع کنیم. این تسک میاد یه متن تو ورودی میگیره و تو خروجی اسم افراد، مکانها، تاریخها و ... رو مشخص میکنه. برای انجام این تسک قرار نیست بیایم از دیکشنری استفاده کنیم. مثلاً بگیم من کلمه پاریس رو داخل دیکشنری دارم، میدونم اسم مکانه، پس هر جا پاریس دیدی با تگ LOC مشخص کن. ممکنه کلمه پاریس اسم فرد هم باشه و همیشه در نقش شهر پاریس نباشه. پس قراره با توجه به متن و context بیایم این تسک رو انجام بدیم.

چجوری با استفاده از شبکههای عصبی میتونیم این تسک رو انجام بدیم؟ روشهای زیادی وجود داره اما یکی از روشهای خیلی ساده برای انجام این تسک اینکه بیایم از یک کلسیفایر باینری استفاده کنیم. قراره یک جمله حاوی کلمه پاریس بهش بدیم و بهمون بگه آیا کلمه پاریس اسم مکان هست یا خیر.
در گام اول میایم طول پنجره مشخص میکنیم تا بدونیم چه تعداد از کلمات راست و چپ کلمه "پاریس" رو قراره بعنوان context در نظر بگیریم. اینجا فرض کنید معادل با 2 هست. یعنی با خود کلمه پاریس مجموعاً 5 تا کلمه داریم. بعد با استفاده از word2vec یا GloVe میدونیم که word embedding این کلماتی که داریم چی هستن. در نهایت embeddingهای پنج تا کلمه رو میدیم به باینری کلسیفایرمون و ازش میخوایم که بهمون بگه آیا کلمه پاریس اسم مکان هست یا خیر.

حالا این کلسیفایری که داریم ازش حرف میزنیم جزییاتش به چه شکله؟ تو اسلاید زیر اومده. اینطوره که تو لایه اول حاوی ورودیمونه (embedding پنج تا کلمه متفاوت). بعد یک لایه شبکه عصبی داریم. این لایه میاد ورودی رو در یک ماتریس به اسم W ضرب میکنه، بعد با یک بایاس جمع میکنه و نتیجه رو میده به یک تابع غیر خطی به اسم f. نتیجه این عملیاتها که با h مشخص میشه تو مرحله بعدی ضرب داخلی میشه با یک ماتریس دیگه به اسم u. خروجی این مرحله یک عدد حقیقیه. در نهایت این عدد حقیقی رو میدیم به یک کلسیفایر که قراره بگه هر کلمه در ورودی با چه احتمالی متعلق به "اسم مکان" هست.

برای اینکه جزییات کلاسیفایر رو بهتر درک کنیم، باید بتونیم گرادیان هم حساب کنیم. برای محاسبه گرادیان هم از دو راه میتونیم استفاده کنیم، یا بشینیم خودمون دستی گرادیان حساب کنیم، یا از یک الگوریتم به اسم backprop استفاده کنیم. تو این جلسه قراره اول ببینیم اگه بخوایم دستی گرادیان بگیریم چطور میشه و بعد با الگوریتم backprop که یکی از مهمترین الگوریتمها در شبکههای عصبی هست آشنا بشیم.

برای روش اول، یعنی محاسبه گرادیان به صورت دستی، باید با یک سری ماتریس و بردار و محاسبات ماتریسی سر و کله بزنیم که برای خیلیا این مباحث خیلی ترسناکه. اگه قرار باشه از ماتریسها استفاده نکنیم، باید از مشتقهای زنجیرهای استفاده کنیم که یک مثال رو هم ازش در جلسه اول دیدیم. ولی کار با ماتریسها و بردارها کار محاسبات رو خیلی برامون سریعتر و آسونتر میکنه، پس برای همین بهتره که یادشون بگیریم!

بریم از صفر شروع کنیم و ببینیم در انتهای این جلسه چند درصد از مباحث ریاضی ترسناک برامون قابل فهم میشه!
فرض کنید تابعی مثل f(x) که تو اسلاید زیر اومده داریم. تابع یک ورودی و یک خروجی داره. تو این حالت گرادیان معادل با همون (شیب) یا مشتق تابعست. به عبارتی دیگه وقتی گرادیان حساب میکنیم میخوایم ببینیم اگه ما ورودی رو یکم تغییر بدیم خروجی تابع چقدر تغییر میکنه؟ چرا این برامون مهمه؟ چون تو شبکههای عصبی مخصوصاً تو تسکای supervised که دیتا و لیبلشون رو داریم، به کمک همین تغییرها میفهمیم که وزنها و پارامترهای مدل رو چجوری تغییر بدیم که بتونیم خروجی تابع هزینه رو کم کنیم.
تو همین مثال ساده اگه ورودی تابع 1 باشه، گرادیان میشه 3. این یعنی اگه ورودی رو نسبت به 1 یه ذره تغییر بدیم (مثلاً 1.01 در نظر بگیریم)، خروجی از 1 میشه حدود 1.03. یعنی تغییر خروجی تقریباً 3 برابر تغییر ورودی بوده (0.03 در برابر 0.01). ولی وقتی ورودی تابع 4 باشه، گرادیان برابر میشه با 48. این یعنی اگه ورودی رو نسبت به 4 یه ذره تغییر بدیم (مثلاً 4.01 در نظر بگیریم)، خروجی از 64 میشه حدود 64.48. یعنی تغییر خروجی تقریباً 48 برابر تغییر ورودی بوده (0.48 در برابر 0.01).

یک قدم جلوتر بریم و ببینیم اگر تابع چند ورودی و یک خروجی داشته باشه گرادیان چطور میشه. تو این حالت گرادیان به جای یک عدد یک برداره که هر مولفهش مشتقهای جزیی تابع نسبت به هر ورودیه. مثلاً مولفهی اول بردار گرادیان، مشتق جزیی تابع نسبت به ورودی x1 هست و همینطور الی آخر. منظور از مشتق جزیی هم همون مشتق عادیه که تو مثال قبلی دیدیم.

حالا اگه تابع n ورودی و m خروجی داشته باشه چی؟ تو این حالت گرادیان دیگه یک عدد یا یک بردار نیست، بلکه به صورت یک ماتریس در میاد. به این ماتریس، ماتریس ژاکوبین گفته میشه و m سطر و n ستون داره. در هر سطر هم مشتقهای خروجی اون سطر نسبت به همهی ورودیها نوشته میشه (سطر اول خروجی اول تابع، سطر دوم خروجی دوم تابع، الی آخر).

حالا بریم سراغ مشتق زنجیرهای و ببینیم اگه ترکیبی از توابع داشته باشیم گرادیان چطور میشه. اسلاید زیر رو ببینید. فرض کنید z تابعی از y باشه و y هم تابعی از x. تو این حالت اگه بخوایم از تابع z نسبت به x مشتق بگیریم باید از قاعده مشتق زنجیری استفاده کنیم. انگار که میایم از توابع جدا جدا مشتق میگیریم و بعد در هم ضربشون میکنیم. یعنی اول میایم از تابع z نسبت به y مشتق میگیریم، بعد از y نسبت به x مشتق میگیریم و در نهایت دو مشتق رو در هم ضرب میکنیم و میشه مشتق z نسبت به x.
حالا اگر توابعی که داریم به جای یک متغیر چند متغیره هم باشن باز در اصل ماجرا فرقی نمیکنه. مثل این میمونه که بیایم ماتریسهای ژاکوبین رو در هم ضرب کنیم.

در ادامه قراره برگردیم به همون مثال کلسیفایرمون که قبلا دیدیم و ببینیم که چطور میتونیم برای توابعی که داشت گرادیان حساب کنیم.
توابع h و z هر کدوم شامل n ورودی و n خروجی هستن، پس ماتریس ژاکوبینی که برای محاسبه مشتق h نسبت به z ساخته میشه یک ماتریس n در n خواهد بود.

حالا اگه بیایم مشتق هر مولفه تابع h رو نسبت به هر مولفه تابع z محاسبه کنیم در نهایت یه یک ماتریس قطری خواهیم داشت. دلیلش هم اینکه فقط وقتی روی قطرها هستیم تغییر ورودی باعث تغییر خروجی میشه، تو بقیه مواقع اینا هیچ تاثیری رو هم ندارن و مشتقشون صفر میشه. (تابع h یک تابع غیر خطی مثل سیگمویده).

حالا اسلاید زیر رو در نظر بگیرید. قراره از Wx+b یکبار نسبت به x و یک بار نسبت به b مشتق بگیریم. تو حالت اول جواب میشه ماتریس W و تو حالت دوم جواب میشه ماتریس همانی. دقت کنید که اینجا با تک متغیر طرف نیستیم. چند ورودی و چند خروجی داریم برای همین ماتریسهای ژاکوبینی هم که ساخته میشه به این صورت در میاد.

برگردیم به شبکه عصبیای که این جلسه رو باهاش شروع کردیم. قراره از تابع s نسبت به b مشتق بگیریم و گرادیان حساب کنیم.
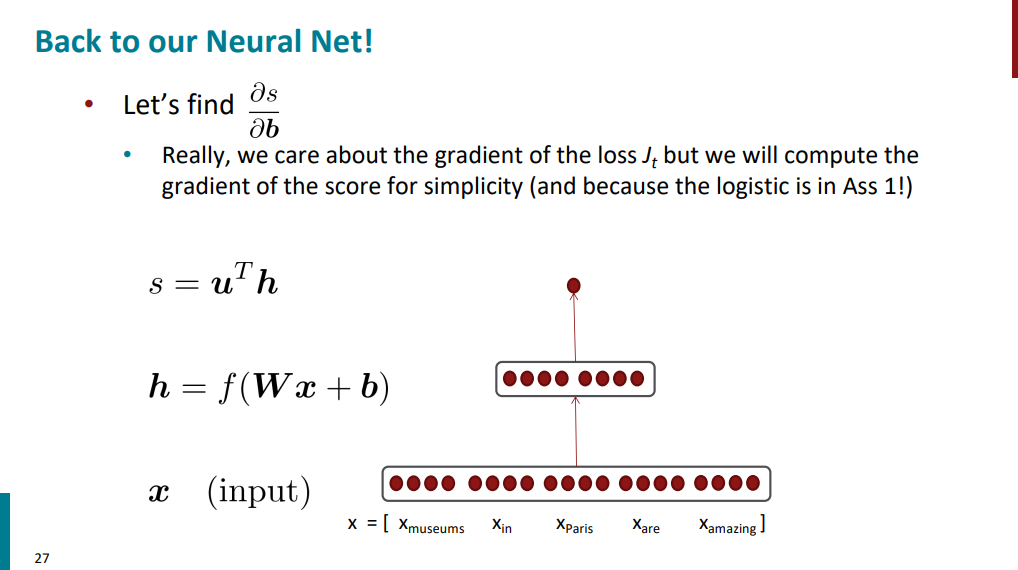
برای اینکه محاسبات سادهتر و تمیزتر بشه، اول میایم متغیری به اسم z تعریف میکنیم:

حالا سه تا تابع از هم دیگه داریم با ورودی x. با استفاده از قانون زنجیرهای میتونیم مشتق بگیریم و گرادیان حساب کنیم.

حالا با توجه به همه مطالبی که تا اینجا دیدیم، طبق اسلاید زیر برای هر قسمت ماتریس ژاکوبین رو محاسبه میکنیم و در نهایت تمامی مقادیر رو در هم ضرب میکنیم (دقت کنید اینجا ضربی که انجام میشه ضرب معمولی ماتریس نیست فرق داره).

از اونجایی که uT برداره و داره در یک ماتریس قطری ضرب میشه، میتونیم بیایم اول ماتریس قطری رو به صورت یک بردار (که ابعادش با بردار uT مطابقت داره) در نظر بگیریم، بعد از ضرب Hadamard یا element-wise product استفاده کنیم. جواب نهایی که به دست میاد یک برداره که حاوی گرادیان s نسبت به پارامتر b عه.

اگه نمیدونید ضرب hadamard چیه شرح مختصری ازش اینجا آورده شده. فرض کنید دو تا بردار یا ماتریس با ابعاد یکسان داشته باشیم میتونیم روش ضرب hadamard رو به صورت زیر اعمال کنیم. یعنی هر المنت رو با المنت متناظرش ضرب کنیم.
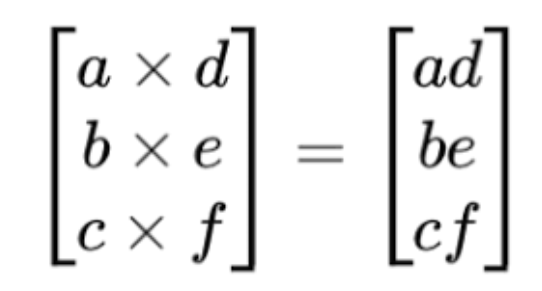
تا اینجا گرادیان s رو نسبت به b حساب کردیم. در ادامه قراره گرادیان s رو نسبت به W محاسبه کنیم. شاید این سؤال پیش بیاد که چرا اصلاً گرادیان s رو نسبت به b و W حساب میکنیم؟ دلیلش اینه که b و W همون پارامترهای مدل هستن، یعنی چیزایی که قرار توی فرآیند یادگیری تنظیم بشن. مدل با تغییر این پارامترها یاد میگیره که پیشبینیهاشو بهتر کنه. به همین دلیل لازمه بدونیم تغییر هرکدوم از این پارامترها چه اثری روی خروجی و در نهایت روی خطا داره. این در واقع همون اطلاعاتیه که از گرادیان به دست میاد.
برای محاسبه گرادیان s نسبت به W هم مشابه مراحل قبلی از مشتق زنجیرهای و ضرب مشتقها در هم استفاده میکنیم. دو بخش اول عیناً مشابه چیزی هست که قبلاً محاسبه کردیم. فقط میمونه مشتق z نسبت به W که جدیده و باید محاسبه کنیم.

همونطور که گفتیم دو بخش اول مشتقها مشابه چیزیه که قبلاً دیدیم و از قبل محاسباتشو انجام دادیم. حالا میایم یک تغییر متغیر میزنیم. متغیری به اسم دلتا تعریف میکنیم و این دو بخش از مشتقهارو که در هم ضرب میشن دلتا مینامیم.

حالا اگه بخوایم گرادیان s نسبت به b و نسبت به W رو بازنویسی کنیم، برای گرادیان s نسبت به b جواب نهایی برابر با همون دلتا میشه. برای محاسبه گرادیان s نسبت به W داریم دلتا در مشتق z نسبت به W. بخش دلتاش که هیچی مشخصه، بخش دوم رو باید حساب کنیم. اگه براتون سواله که چرا اومدیم دلتا تعریف کردیم و تغییر متغیر انجام دادیم بخاطر اینکه از محاسبات تکراری جلوگیری کنیم. یکبار دلتا رو حساب میکنیم و هر دفعه که بخوایم ازش استفاده میکنیم.

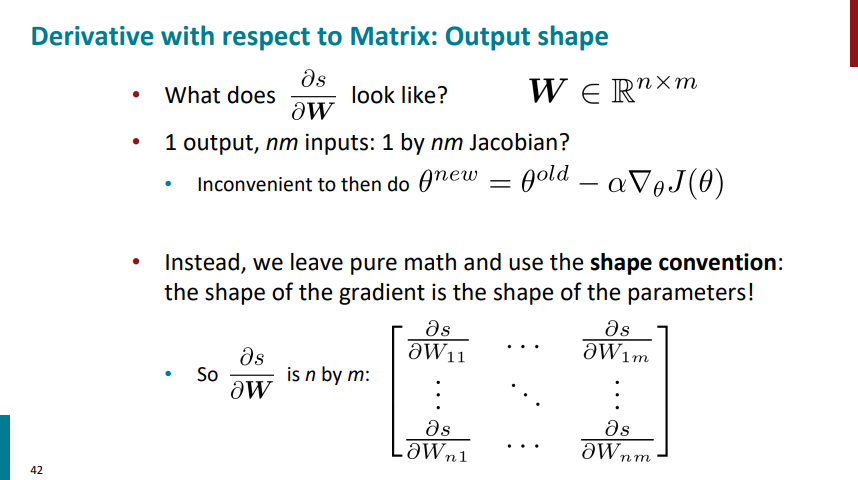
یک بار دیگه گرادیان s نسبت به W رو بررسی کنیم. اگه از ریاضیات محض برای محاسبات استفاده کنیم، ماتریس ژاکوبینِ گرادیان s نسبت به W حاوی یک سطر و n*m ستون خواهد بود. منتها این ماتریس رو نمیتونیم با بردار W که ابعادش n در m هست ضرب ماتریسی کنیم برای همین باید ابعادش رو تغییر بدیم به ماتریسی با n سطر و m ردیف. چرا این موضوع برامون مهمه؟ چون قراره در نهایت وزنهای مدل رو با استفاده از گرادیان کاهشی آپدیت کنیم و لازمه گرادیان همشکل خود وزنها باشه.
گفتیم که برای محاسبه گرادیان s نسبت به W داریم: دلتا در مشتق z نسبت به W. بخش دلتاش که هیچی مشخصه، بخش دوم رو باید حساب کنیم. میدونیم که z در واقع تابعی از W و x عه. پس اگه ازش نسبت به W مشتق بگیریم، جواب میشه x. پس برای جواب نهایی گرادیان s نسبت به W داریم دلتا در x.

ممکنه سوال پیش بیاد چرا داریم ترانهاده حساب میکنیم بعد ضرب میکنیم؟ فقط برای حفظ ابعاد ماتریس خروجیه، دلیل خاصی نداره. توضیحات بیشتر رو بالاتر در موردش خوندیم. خروجی نهایی این گرادیان باید ابعادش n در m باشه.

بالاتر گفتیم که برای محاسبه گرایان s نسبت به W نیاز داریم که از shape convention استفاده کنیم و ریاضیات محض رو کنار بذاریم و ابعاد ماتریس ژاکوبین رو تغییر بدیم. به صورت مشابه برای محاسبه گرادیان s نسبت به b هم نیاز داریم این کار رو بکنیم. چون اگه با ریاضیات محض پیش بریم خروجی فقط یک ماتریس سطری میشه در حالیکه برای محاسباتمون چیزی که در نهایت نیاز داریم یک ماتریس ستونیه.

به طور کلی به دو صورت میتونیم از این قاعده تغییر ابعاد (shape convention) استفاده کنیم.
اول اینکه بیایم با استفاده از ریاضیات محض تمام محاسبات رو در قالب ژاکوبین انجام بدیم و در نهایت ابعاد خروجی رو به اون چیزی که میخوایم تبدیل کنیم.
یا هم اینکه از اول قانون شکل رو دنبال کنیم و تو هر مرحله ببینیم ابعاد چهطوری باید باشه، یعنی مرحلهبهمرحله ابعاد رو رعایت کنیم و هرجا لازم بود transpose یا reshape انجام بدیم.
روش دوم معمولاً عملیتره چون همزمان با پیشروی محاسبات، تضمین میکنه که نتیجه نهایی همشکل پارامترهای مدل (مثلاً W) میشه.

در ادامه قراره با backpropagation, forward propagation و گراف محاسباتی آشنا شیم، و ببینیم که چی هستن.
اگر ادامه مطالب رو خوندین و تو یک حالت گنگی به سر بردین و خیلی براتون ملموس نبود، باید بگم کاملاً طبیعیه و نگران نباشید! مباحث واقعاً تخصصی ان و این حس عدم فهمیدن خیلی طبیعیه! منتها اگر دانشجوی کامپیوتر یا هوش مصنوعی هستین، یا تو این حوزه مشغول به کارید، اگه رک بخوام بگم، حقیقتاً زشته که این چیزارو بلد نباشید، انقدر گیر بدین تا متوجه بشین! ولی اگه صرفاً خواننده مشتاقید و میخواید یه دید کلی از این مباحث پیدا کنید، حتی اگه خیلی هم متوجه داستان نشدید اهمیتی نداره!
تا به اینجای کار یه جورایی با این الگوریتم آشنا شدیم. ایدهش اینکه بیاد مشتقها و گرادیانهایی رو که تو لایههای بالاتر گرفتیم نگه داره و بعد تو لایههای پایینی اگه دوباره نیاز به اون مقادیر داشتیم از همونا مجدد استفاده کنه، به جای اینکه بیاد دوباره از اول مشتق حساب کنه. یه جورایی سرعت انجام کار رو با کمتر کردن تعداد محاسبات بیشتر میکنه. در ادامه جزییات بیشتری ازش رو میبینیم.

اگر بخوایم توابع ریاضی رو با استفاده از نمودار نشون بدیم، در واقع یک گراف محاسباتی رسم کردیم. برای مثال گراف زیر داره تابعی رو نشون میده که از اولِ این جلسه مورد بررسی قرار دادیم. روی یالها ورودی و خروجی مشخص میشه و هر نود هم نشون دهندهی عملیاتهای ریاضیه.
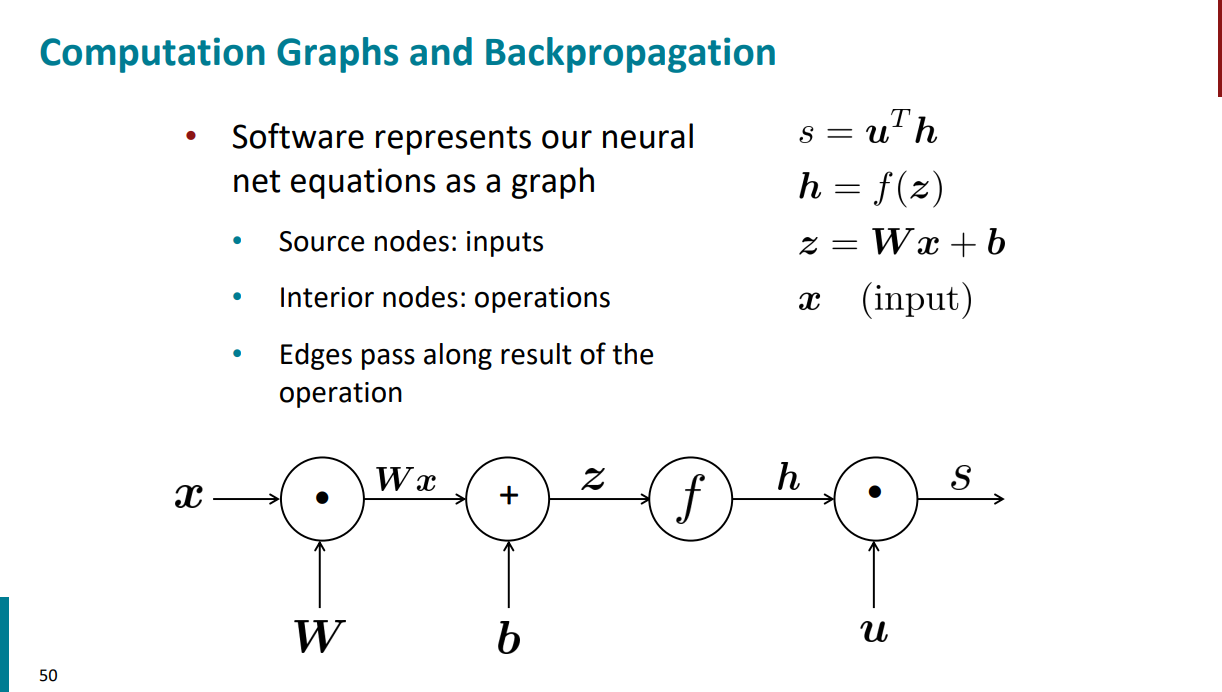
با یک مثال توضیح راحتتری داره. گراف محاسباتی اسلاید قبل رو در نظر بگیرید. اگر به ازای ورودیهای مختلف شروع کنیم از چپ به راست بیایم و جواب نهایی رو برای s حساب کنیم، در واقع داریم forward propagation انجام میدیم.

حالا اگر مراحلی رو که از چپ به راست اومدیم، از راست به چپ بریم و تو هر مرحله مشتق بگیریم، داریم backward propagation انجام میدیم.
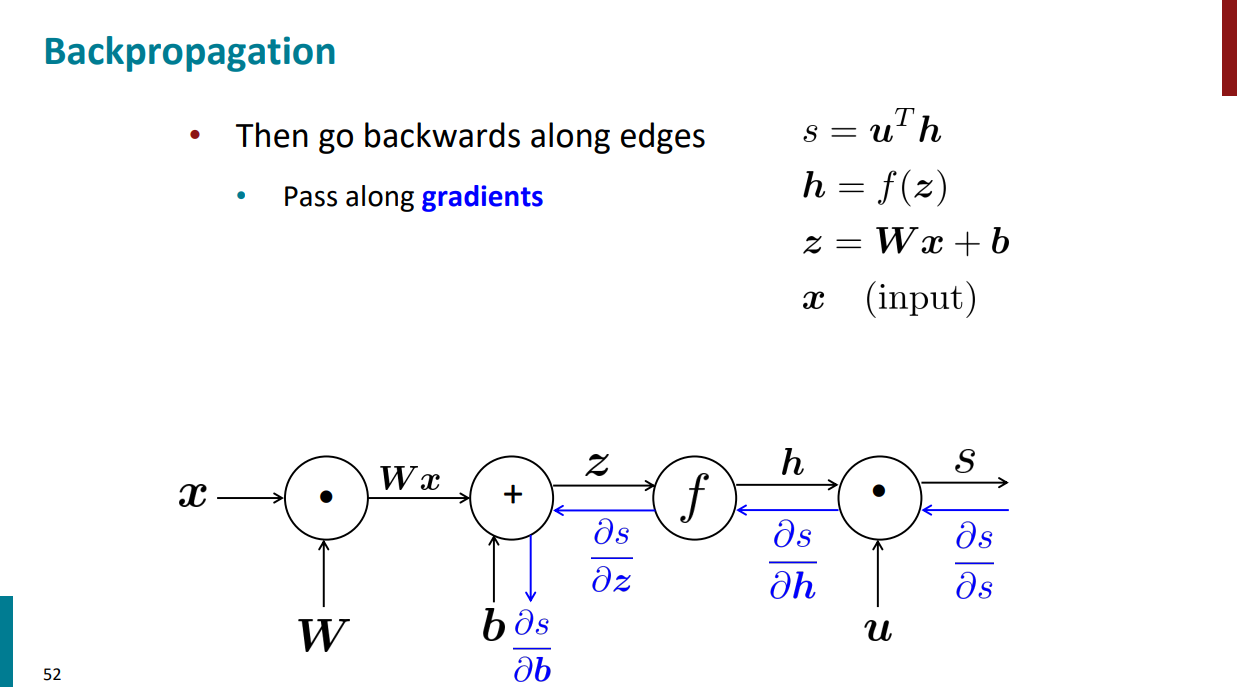
هر نودی که تو گراف محاسباتی داریم، خودش هم شامل یک گرادیان محلیه. بالاتر دیدیم که چطور میتونیم با استفاده از قاعده مشتق زنجیری از s نسبت به z مشتق بگیریم. دقیقاً همون مراحل با استفاده از گراف محاسباتی اینجا هم آورده شده.
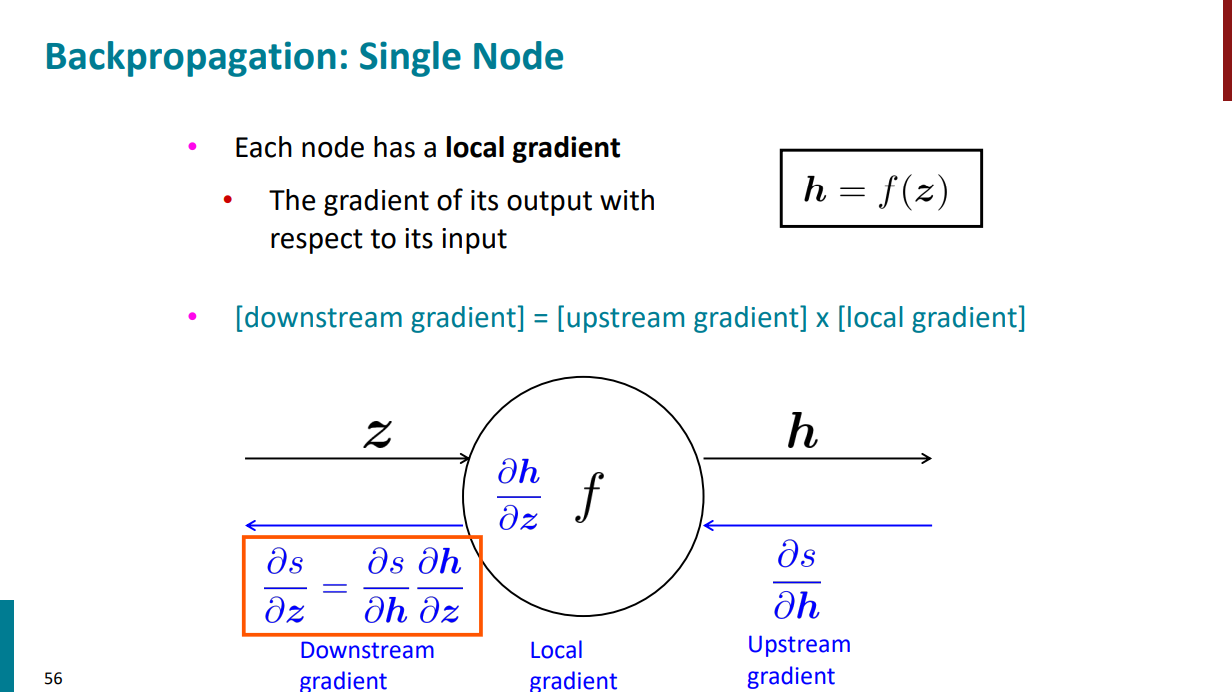
مثالی که بالا هست فقط یک ورودی و یک خروجی داره، حالا اگر دو تا ورودی داشته باشیم محاسبه گرادیانها به چه شکل میشه؟ در واقع اینجا هم همونه. با این تفاوت که چون دو تا ورودی داریم، باید دو تا هم گرادیان محلی حساب کنیم.
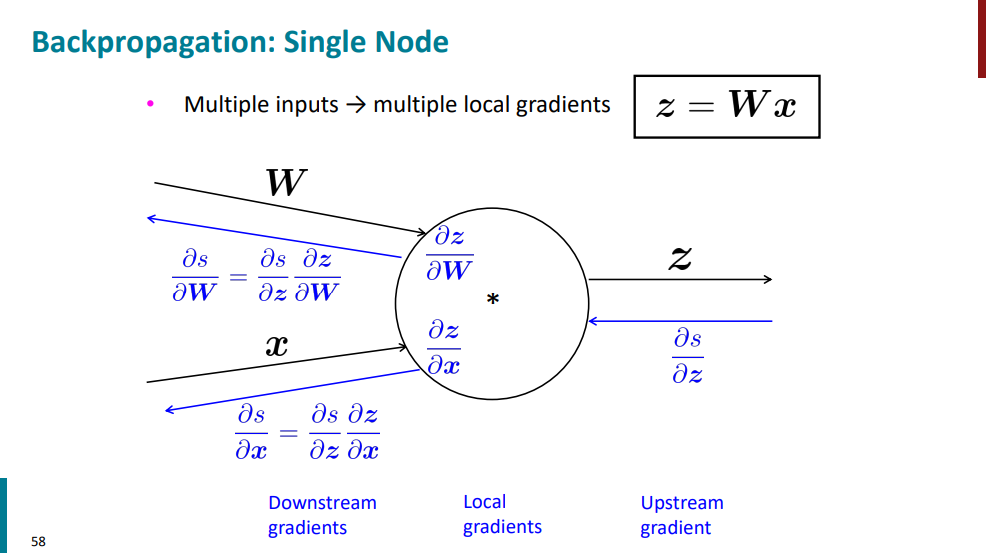
ممکنه گیج شده باشین که چرا داریم این کارا رو میکنیم؟ اصلاً هدف چیه؟ فهمیدیم که گراف محاسباتی و forward propagation و backward propagation چی هستن به خودی خود، ولی خب قراره در نهایت چیکارشون کنیم؟ این جلسه رو با یه شبکه عصبی ساده شروع کردیم و تا همینجا هم داریم روی همون صحبت میکنیم. کل کار الگوریتمهای یادگیری ماشین و شبکههای عصبی اینه که میان بر اساس دادههای ورودی (تو مثال ما x)، یه سری وزن یا پارامتر (تو مثال ما W و b) برای مدل یاد میگیرن. توی هر مرحله اول یه بار forward propagation انجام میشه و خروجی مدل محاسبه میشه، بعد از اینکه مقدار تابع خطا مشخص شد (یعنی فهمیدیم که مقدار واقعی چقدر با چیزی که مدل محاسبه کرده و خروجی داده فرق داره)، مدل باید وزنها رو آپدیت کنه و backward propagation بزنه. وزنها به کمک گرادیانها و مشتق گرفتن آپدیت میشن و این چرخه همینطور ادامه پیدا میکنه تا جایی که مدل به بهترین مقدار برای پارامترهاش برسه.
در ادامه باهم یک مثال خیلی ساده رو بررسی میکنیم. تو دنیای واقعی شبکههای عصبی به این شکل ساده نیستن و خیلی خیلی پیچیدهترن. هدف اینجا صرفاً اینکه بفهمیم الگوریتمهای backpropagation, forward propagation دقیقاً چجوری کار میکنن.
فرض کنید تابعی داریم به شکل زیر (دو متغیر x و y رو باهم جمع میکنه، حاصلش رو ضرب میکنه در مقدار بیشینه بین y و z) که مقادیر اولیه هم براش تعیین شده:
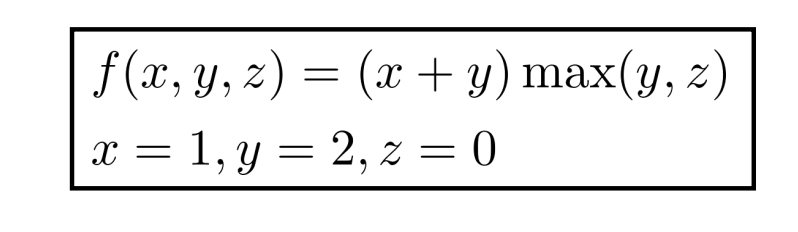
اول میایم گراف محاسباتیشو رسم میکنیم که بعدا کار مشتق گرفتن برامون راحتتر بشه:
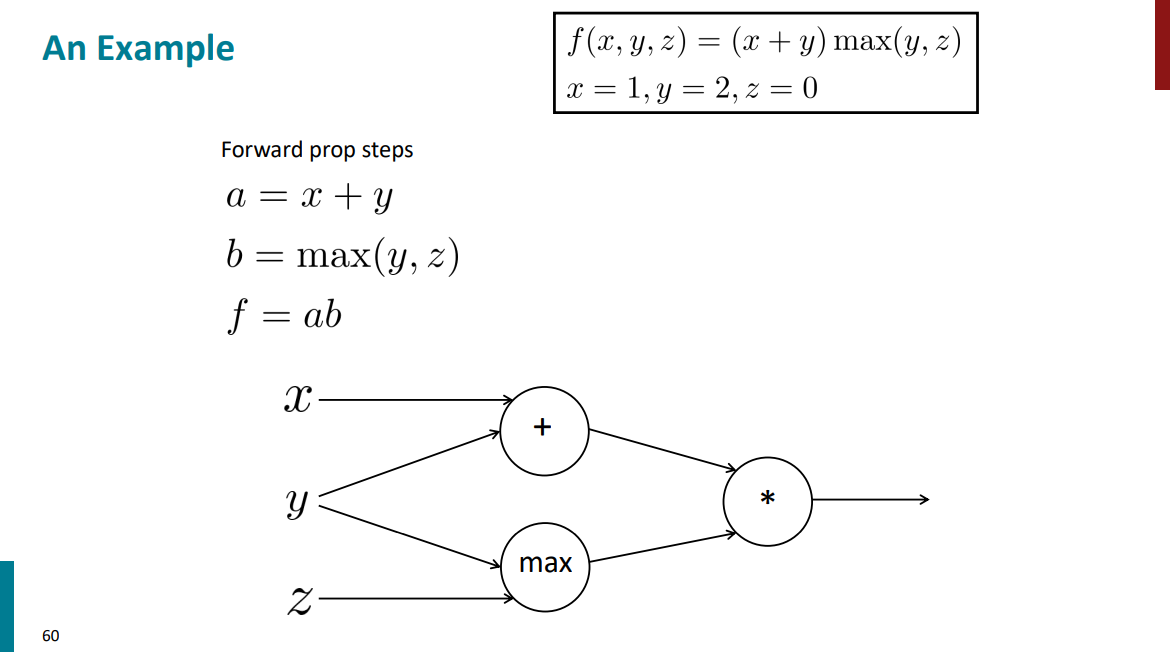
برای مرحله forward propagation فقط کافیه بیایم با مقادیر اولیهای که برای ورودیها داریم همه چیز رو حساب کنیم بریم جلو:
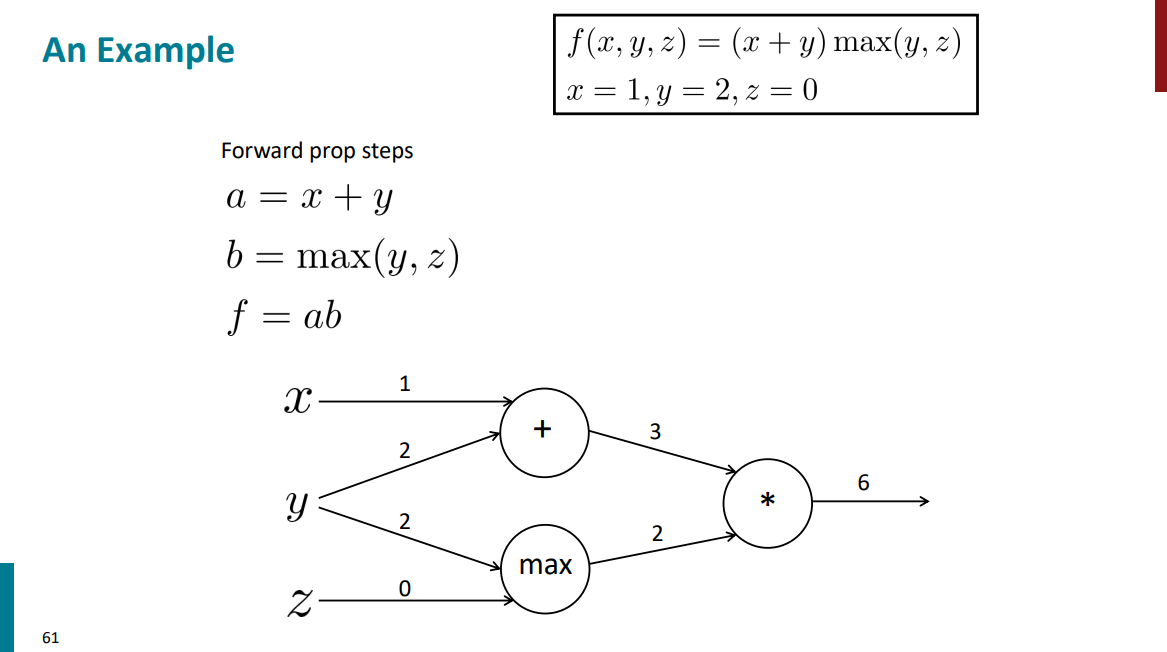
از اینجا به بعد قراره ببینیم backward propagation به چه صورت میشه. قراره از عقب به جلو مشتق بگیریم و پیش بریم. قبل از هرچیزی باید اول مشتقهای محلی رو حساب کنیم.
اول بریم سراغ عبارت a. مشتق a نسبت به x میشه 1 و مشتق a نسبت به y هم میشه 1.
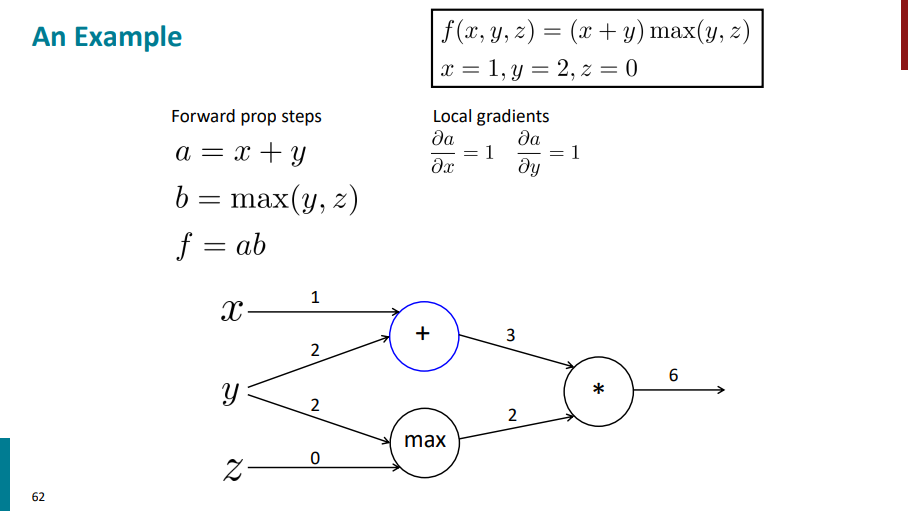
حالا بریم سراغ عبارت b. اگر از b نسبت به y مشتق بگیریم حاصل میشه:
= 1(y > z) = 1
چون تو این حالت مقدار اولیه y و z به صورتی هست که مقدار y از مقدار z بیشتره (y=2 , z=0)، پس شرط داخل پرانتز true میشه و جواب نهایی میشه یک.
اگر از b نسبت به z مشتق بگیریم میشه:
= 1(z > y) = 0
بخاطر مقدار اولیه y و z شرط داخل پرانتز false میشه و جواب نهایی میشه صفر.
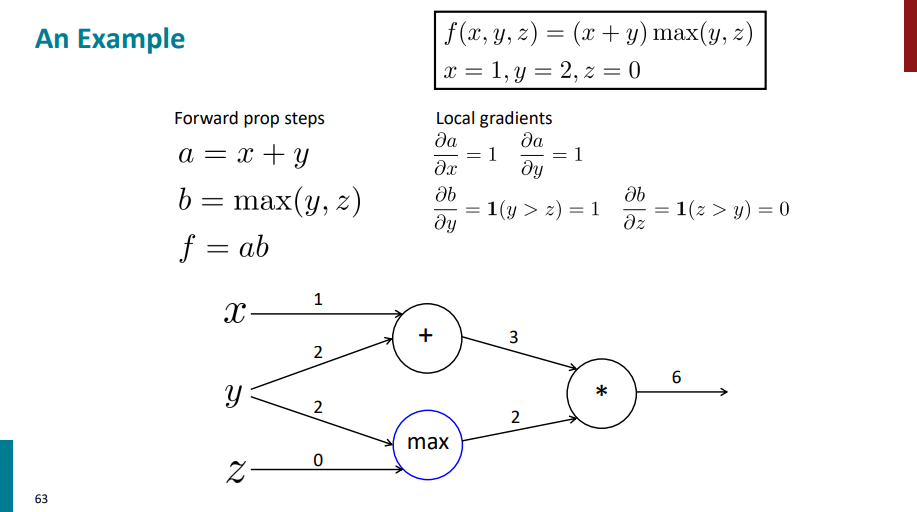
حالا بریم سراغ نود آخر که معادله با عبارت f. اگر از f نسبت به a مشتق بگیریم، جواب میشه b و اگر از f نسبت به b مشتق بگیریم جواب میشه a. چون مقادیر رو برای a و b حساب کردیم و از قبل میدونیم، پس به ترتیب جواب نهایی برای مشتقها میشه 2 و 3.
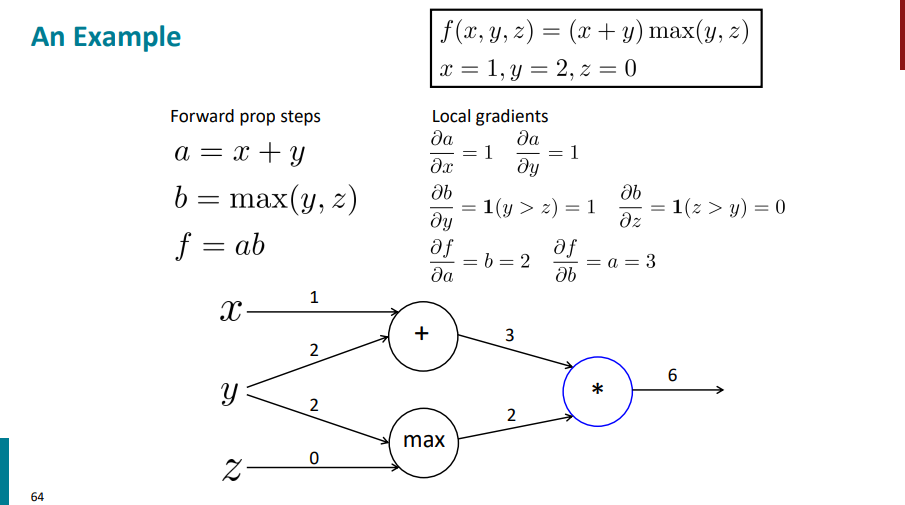
حالا، که مشتقهای محلی رو محاسبه کردیم، میریم سراغ مشتق گیری از آخر به اول. اولین مشتقی که باید حساب کنیم، مشتق f نسبت به خودشه که میشه 1.
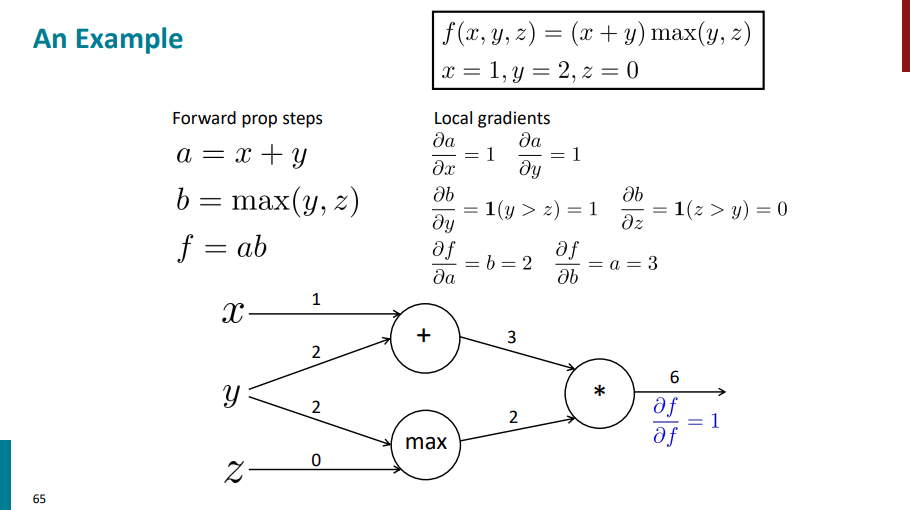
بعد میریم سراغ مشتق زنجیرهای حساب کردن. تو هر مرحله مشتق لایه بالایی در مشتقهای محلی ضرب میشه. مشتق لایه بالایی تو این مرحله میشه مشتق f نسبت به خودش که برابر هست با 1 و مشتقهای محلی برای هر یال که تو مراحل قبلی حساب کردیم (مشتق f نسبت به a و مشتق f نسبت به b) برابره با 2 و 3. وقتی دو تا مشتق محلی و لایه بالاتر رو در هم ضرب کنیم (در واقع استفاده از همون قاعده زنجیری) جوابهای نهایی برای این لایه به ترتیب میشه 2 و 3.
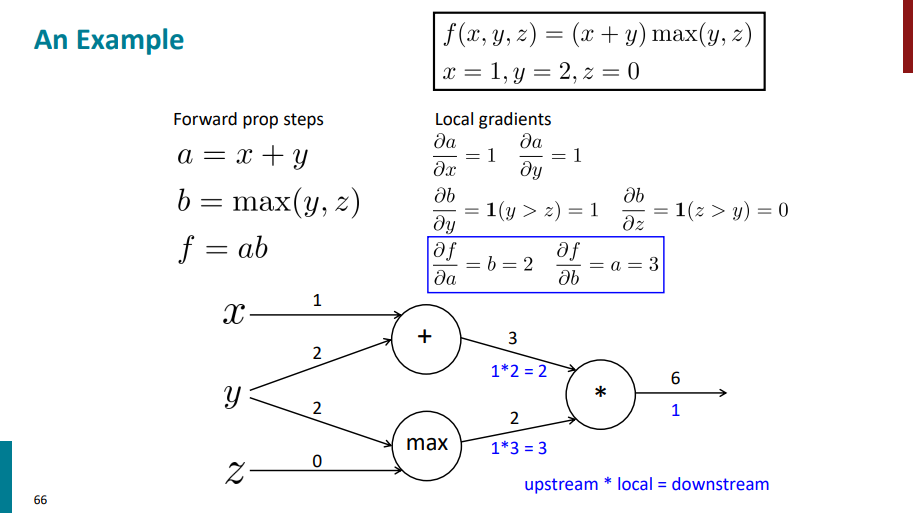
حالا یک لایه دیگه برمیگردیم عقبتر. اول محاسبات رو برای نود max انجام میدیم. تو این مرحله مشتق لایه بالایی در واقع همون مشتقهای زنجیری هست که تو مرحله قبلی حساب کردیم. یک سری مشتق محلی هم داریم که از قبل حساب کردیم (مشتق b نسبت به y و مشتق b نسبت به z). حالا باید مشتقهای محلی رو در مشتق یک لایه بالاتر ضرب کنیم تا مشتق نهایی این لایه هم به دست بیاد.
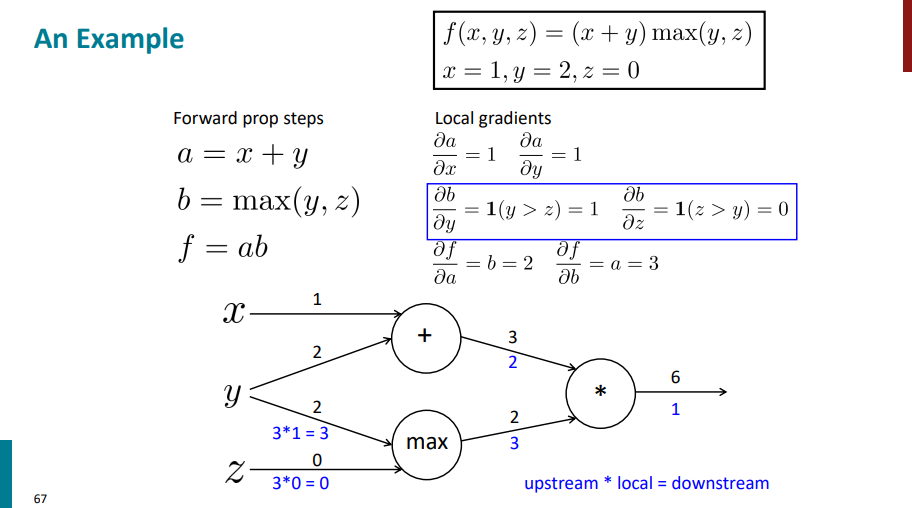
به صورت مشابه محاسبات رو برای نود + هم باید انجام بدیم.
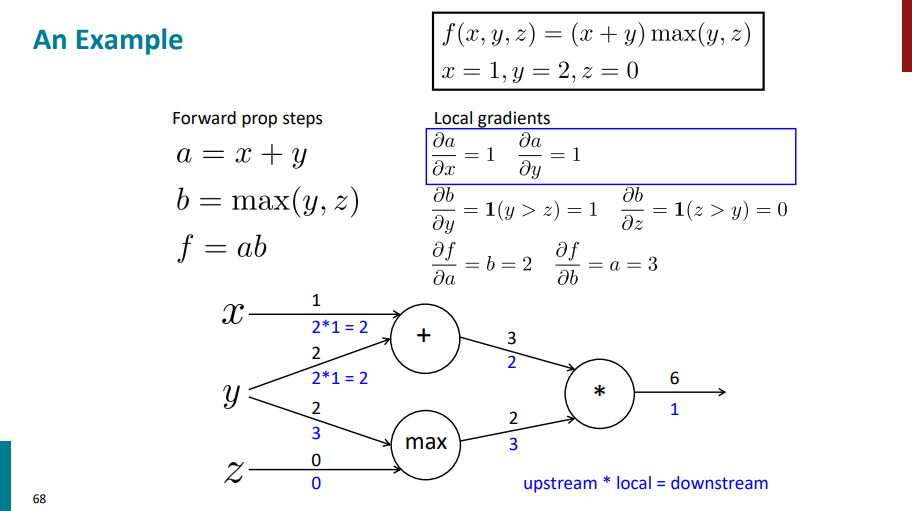
این همه مشتق گرفتیم و حساب کتاب کردیم تا اینکه در نهایت باید بیایم مشتق خروجی (f) رو نسبت به ورودیهامون (x, y, z) حساب کنیم:
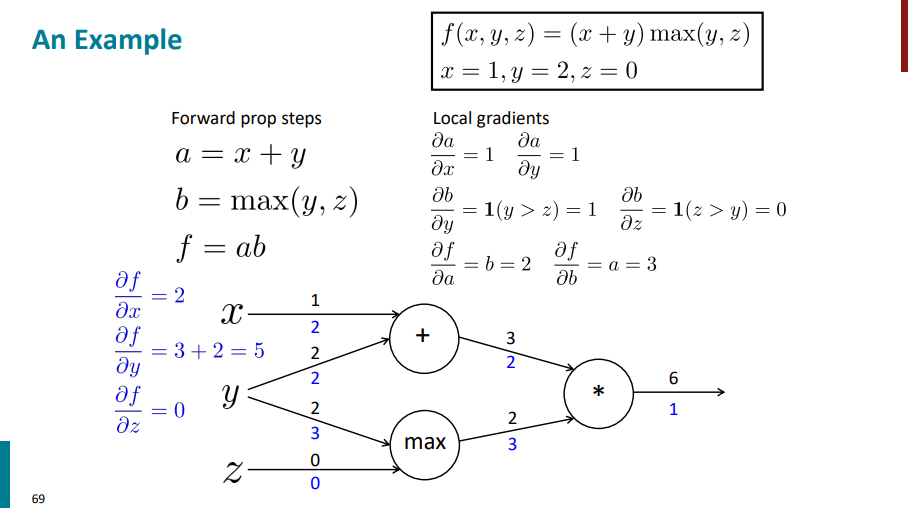
حالا این گرادیانهایی که حساب کردیم داره چیو نشون میده؟ داره نشون میده که تغییرات کوچیک هر متغیر ورودی چه اثری روی خروجی تابع f داره. مثلاً مشتق f نسبت به z شده 0. این یعنی چی؟ یعنی اینکه اگه ما بیایم مقدار z رو از مقدار اولیه 0 یکم تغییر بدیم به یه مقدار دیگه، بخاطر اینکه مشتق (گرادیان) f نسبت بهش 0 شده، تاثیر خاصی روی خروجی تابع f نمیذاره. به عبارت دیگه، گرادیانها بهمون میگن کدوم ورودیها مهمترن و چقدر تغییرشون خروجی رو تکون میده.
برگردیم به ادامه مثال. اما قبلش باید یک قانون کلی رو بررسی کنیم.
اگه از یک نود دو تا یال خارج شده باشن، موقع انجام backward propagation و محاسبه گرادیانها در واقع دو تا یال به اون نود وارد شدن. پس در نهایت باید گرادیانهایی که برای اون نود داریم رو باهم دیگه جمع کنیم.
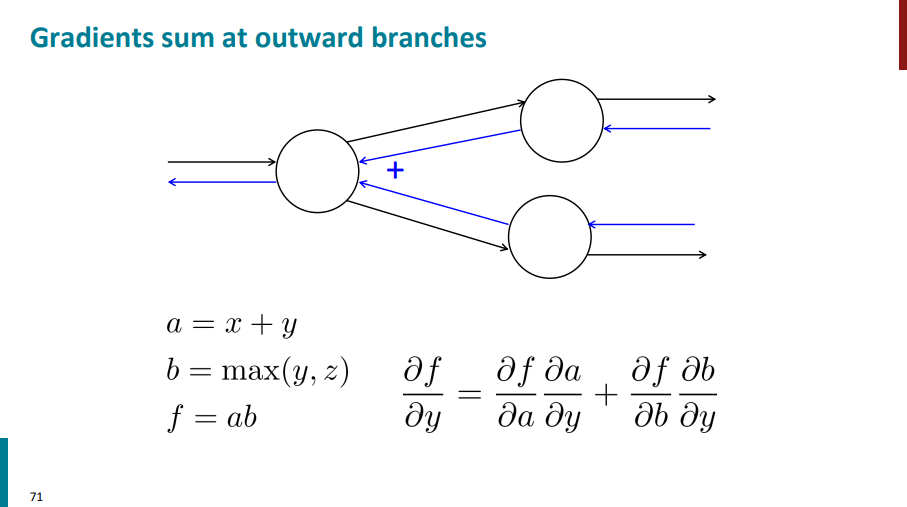
برگردیم به مثالی که داشتیم و از یه زاویه دیگه نودها و گرادیانهارو بررسی کنیم. چرا؟ برای اینکه اگه نخوایم تو هر مرحله دستی گرادیانهارو حساب کنیم با دونستن این قوانین میتونیم گرادیانهارو خودمون از لایههای بالاتر به لایههای پایینتر انتقال بدیم.
نودی که علامت جمع داره گرادیان لایه بالایی رو (گرادیان با رنگ آبی روی یالی که ازش خارج شده آورده شده) روی یالهای ورودی توزیع میکنه.
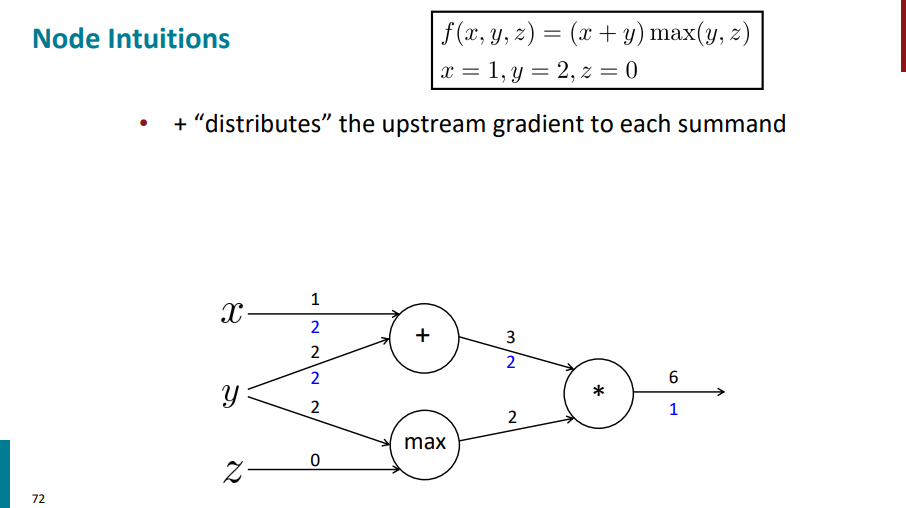
نودی که max داره مقدار گرادیان لایه بالاتر رو به یالی که عدد ورودی بیشتری داره اساین میکنه و یال دیگه مقدار گرادیانش 0 میشه.
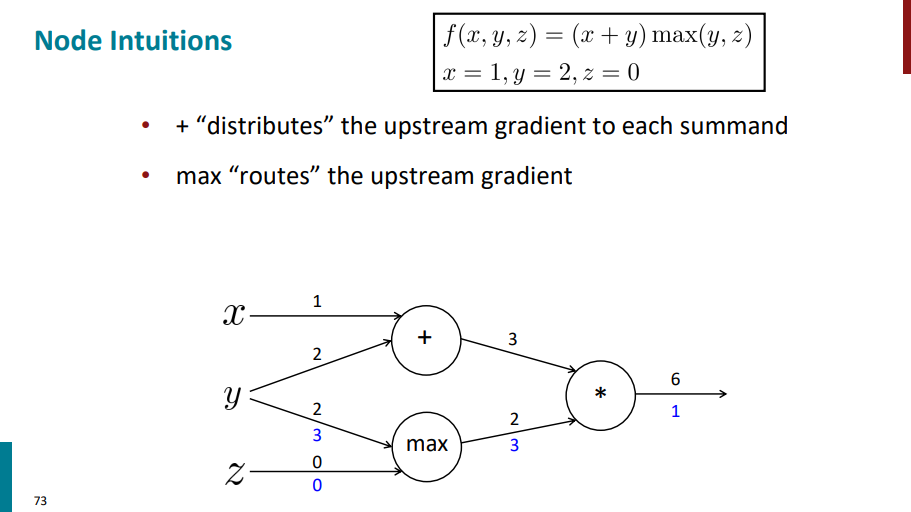
یالی که علامت ضربدر (یا ستاره) داره گرادیان لایههای پایینترش میشه برعکس مقدار ورودیشون. مثلاً ورودی یال بالا 3 بوده و ورودی یال پایین 2، گرادیان یال بالایی میشه 2 و گرادیان یال پایینی میشه 3.
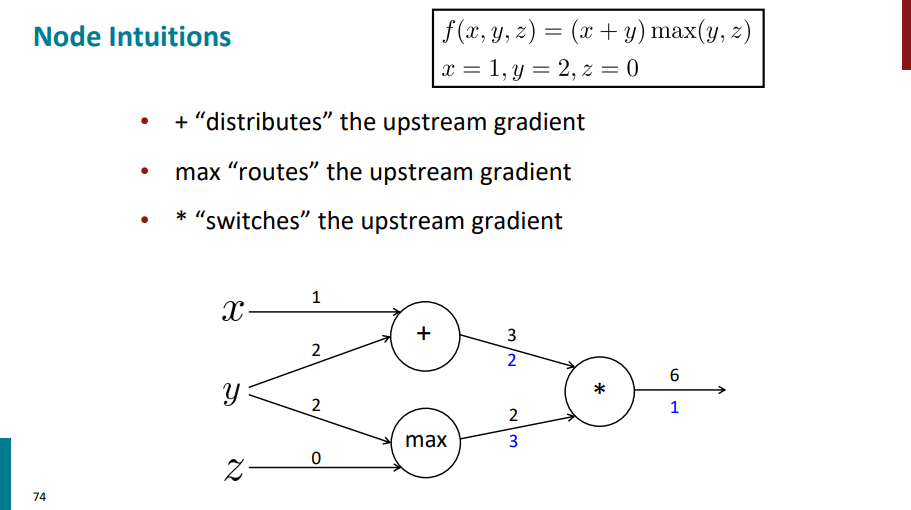
گفتیم دلیل معرفی الگوریتم backward propagation این بوده که باعث بشه دیگه محاسبات تکراری رو برای گرادیانها بارها و بارها انجام ندیم. قراره تو سه تا اسلاید پایین با شکل ببینیم که این حرف یعنی چی!
فرض کنید برای محاسبه گرادیان s نسبت به b بیایم مسیر آبی رنگ رو که تو اسلاید زیر آورده شده از راست به چپ طی کنیم.
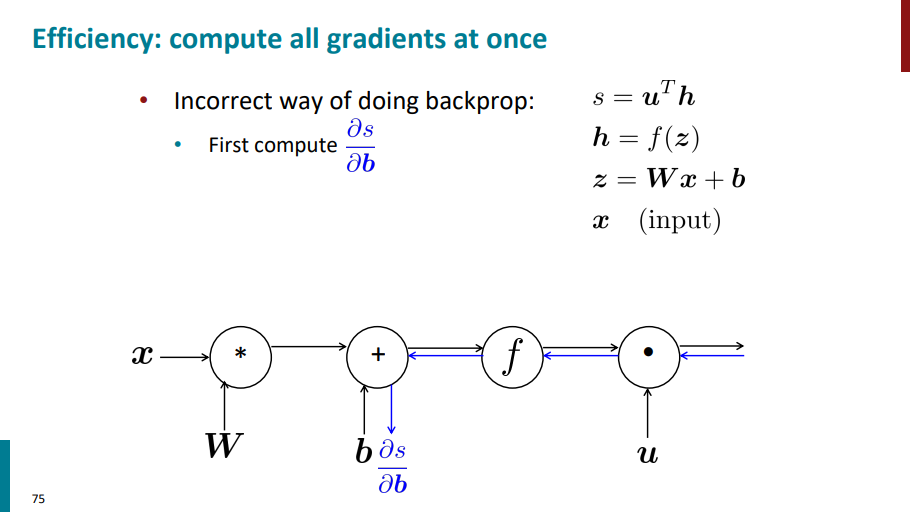
بعد برای محاسبه گرادیان s نسبت به W هم مجدداً بیایم مسیر قرمز رنگ رو از سمت راست طی کنیم به سمت چپ بریم و گرادیان حساب کنیم. این کار درستی نیست! چون داریم یک سری محاسبات رو بارها و بارها تکرار میکنیم و استفاده نادرست از منابعمون میکنیم.
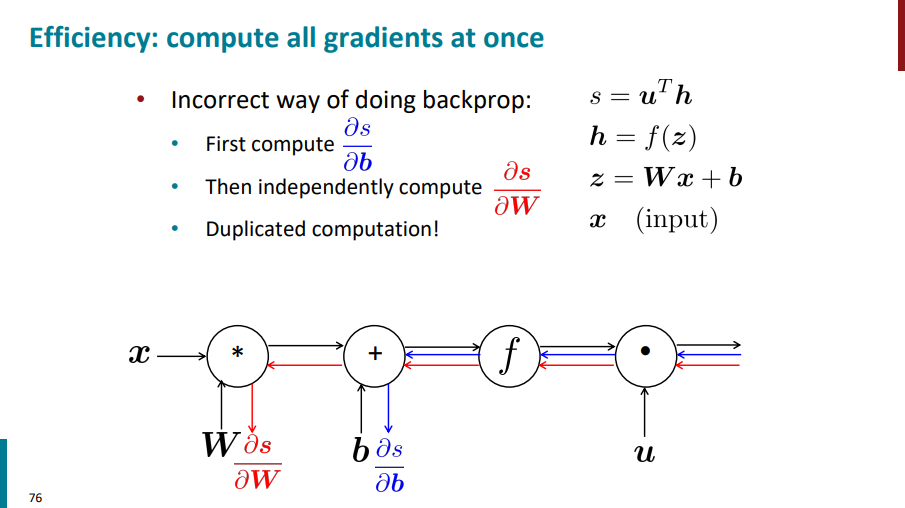
برای اینکه چند بار چند بار گرادیان تکراری حساب نکنیم، میایم برای هر مرحله یک بار گرادیان حساب میکنیم و گرادیان حساب شده رو داخل یک متغیر دیگه نگه میداریم (مثلاً خیلی بالاتر اومدیم متغیر دلتا رو معرفی کردیم). با این کار دیگه نیاز نیست هر دفعه گرادیان حساب کنیم. یک بار محاسبات انجام میشه، دفعههای بعدی از مقدار استفاده شده فقط استفاده میکنیم.
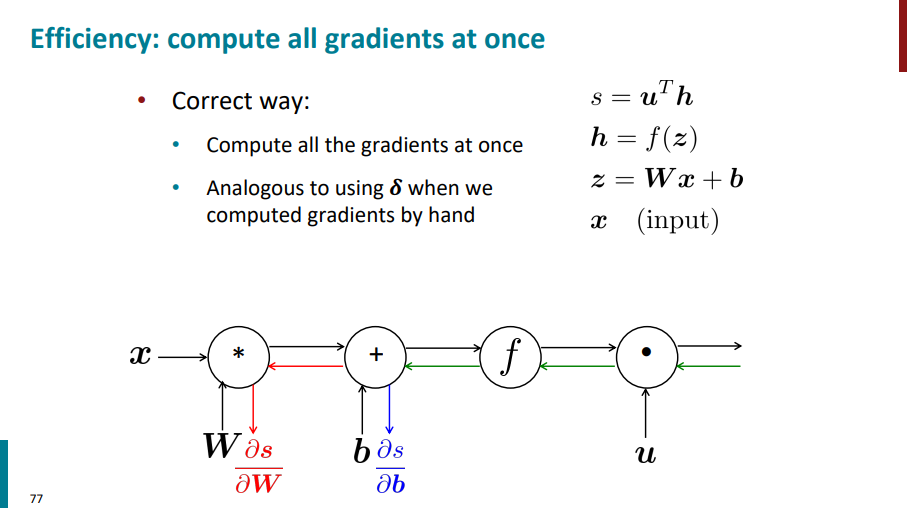
به صورت کلی اگر یک گراف عمومی داشته باشیم، اول از نودهای ورودی شروع میکنیم و به سمت نودهای خروجی میریم و تو هر مرحله، مقداری که هر نود داره رو محاسبه میکنیم. تا اینجا میشه فاز forward propagation.
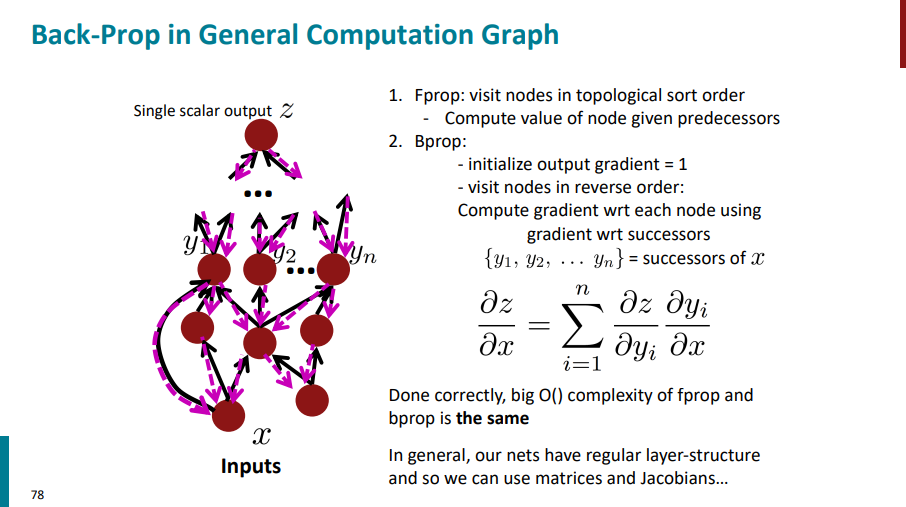
بعد برای فاز backward propagation از ته گراف (خروجی) شروع میکنیم و به سمت سر گراف (ورودی) میایم. اولین مقداری که برای گرادیان حساب میشه، همیشه 1 هست، چون مشتق یک تابع نسبت به خودش برابر با یکه. داریم از ته به سر میایم و گرادیان هر نود رو محاسبه میکنیم. اگر از یک نود چند یال خارج شده باشه، در واقع موقع برگشت چند یال بهش وارد میشه (خطچینهای صورتی)، پس همهی مشتقهای مربوط به اون نود رو با هم جمع میکنیم.
اگر تمام این کارها رو به درستی انجام بدیم، از نظر پیچیدگی زمانیِ محاسبات، الگوریتم f-prop با الگوریتم b-prop یکی میشه و هر دو از مرتبهی O(n) خواهند بود.
توی سیستمها و فریمورکهایی که توسعه داده شدن، دیگه نمیان دستی گرادیان حساب کنن. کاری که اینجا انجام میشه به این صورته که یک بار f-prop انجام میشه و خروجی هر نود محاسبه میشه. بعد، رابطهی ریاضی بین ورودی و خروجی اون نود هم به دست میاد. در نهایت، از روی همین روابط و بدون اینکه نیاز باشه خودمون کاری برای محاسبهی گرادیانها انجام بدیم، سیستم بهصورت خودکار فرمولهای گرادیان رو استخراج میکنه.
تمام چیزی که هر نود در یک گراف باید بتونه حساب کنه اینه که:
چطوری خروجی خودش رو از روی ورودیها به دست بیاره.
وقتی گرادیان خروجی (مشتق نسبت به خروجی) بهش داده شد، چطوری گرادیان نسبت به ورودیهاش رو حساب کنه.
توی فریمورکهایی مثل PyTorch یا TensorFlow که برای کار با شبکههای عصبی ساخته شدن، کل فرآیند b-prop بهصورت خودکار انجام میشه. تنها کاری که لازمه دولوپر بکنه اینه که وقتی یه نود جدید اضافه میکنه، حواسش باشه مشتق محلی (local derivative) اون نود رو هم مشخص کنه. بقیهی فرآیند خودش انجام میشه.

برای مثال یه تیکه کد در اسلاید پایین آورده شده که نشون میده چطور باید از گراف محاسباتی استفاده کرد برای انجام f-prop و b-prop. مثلاً تو مرحله f-prop نیازه که ورودیهای گراف رو خودمون مشخص کنیم. اما بقیه مراحل به کمک توابع از قبل تعریف شده قابل انجام هستن.

فرض کنید نود ضرب (یا ستاره) داریم با دو تا ورودی x و y و خروجی z. تابع f-prop مشخصاً میاد ورودیهارو میگیره و ضرب میکنه تو هم و خروجیشو میریزه داخل z. حالا برای قسمت b-prop باید حواسمون باشه که مشتقهای محلی رو باید خودمون دستی تعریف بکنیم. تا در نهایت بتونیم مشتق خروجی رو نسبت به ورودیها داشته باشیم.
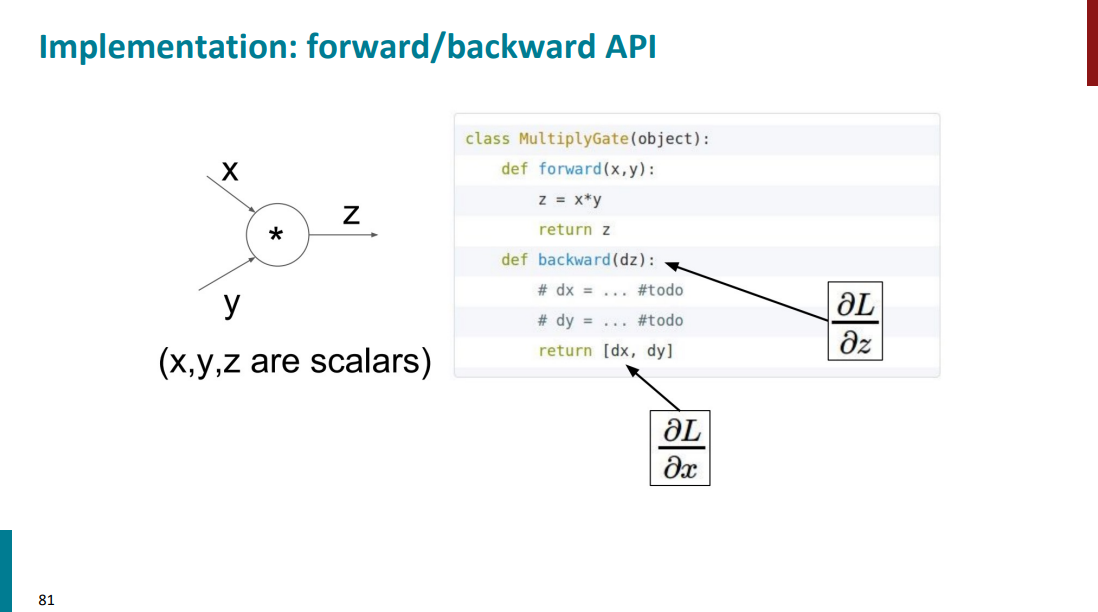
از طرفی دیگه از اونجایی که به خود مقادیر x و y هم نیاز داریم، باید حواسمون باشه که همون اول یه جایی ذخیرهشون بکنیم.

تمام این پروسه محاسبه گرادیانها و نودها که تو کل این جلسه بررسی کردیم همشون به صورت automated انجام میشن، هیچوقت به صورت دستی نمیایم تو یک شبکه عصبی واقعی این موارد رو محاسبه کنیم. اما نیازه که جزییات محاسبات رو بلد باشیم و بدونیم که اگر بخوایم دستی محاسبهشون کنیم روند به چه صورت خواهد بود. گاهی نیازه به صورت دستی محاسبات رو چک کنیم و گرادیان بگیریم تا مطمئن بشیم چیزی که پیاده سازی کردیم داره درست کار میکنه.

با ساز و کار شبکههای عصبی آشنا شدیم و دیدیم که چطور کار میکنن و چه ارتباطی با مشتق و گرادیان حساب کردن دارن. دیدیم که گراف محاسباتی، backward propagation و forward propagation چی هستن.

اگر جایی ایراد یا مشکلی بود، حتماً بهم بگید تا تصحیح کنم. اگر هم پست رو دوست داشتید و محتواش به دردتون خورد، میتونید یه قهوه مهمونم کنید!