اتومات های سلولی: اتم های پیچیدگی

وقتی با پدیده های پیچیده روبرو می شویم یکی از راهها برای فهم آن را تقسیم به اجزای سازنده می دانیم. مثلا وقتی چیزی مثل بدن انسان را درک نمیکنیم سعی میکنیم به سطح قسمت های سازنده آن مانند معده، روده، قلب و مغز برویم و اگر باز هم توضیحات بیشتر می خواهیم می توانیم باز هم جزیی تر نگاه کنیم تا اینکه به سطح سلولی برسیم. این کار را تقریبا برای هر شاخه ای از شناخت علمی انجام می دهیم. مثلا اگر درک جامعه پیچیده است سعی میکنیم آن را در سطح گروه ها و افراد ببینیم یا اگر به طور کلی جهان پیچیده است آن را تا سطح اتم و الکترون و کوارک فروکاهش دهیم و بعد مطالعه کنیم. البته این یک واکنش نسبتا طبیعی با توجه به موفقیت های علمی در سده های اخیر است. رویه علمی برای قرن ها بر اساس فرض "فروکاست گرایی"(reductionism) قرار گرفته است. در این دیدگاه متافیزیکی، فهم هر چیزی با جراحی کردن و تقسیم آن به اجزای سازنده اش که ساده تر هستند، قابل انجام است. این تز متافیزیکی البته همیشه بدون چالش هم نبوده است. یکی از نمونه های آن تلاش علم برای کاهش به سطح زیر اتمی بود. نتیجه چنین تلاشی برعکس شد: نه تنها اجزا ساده تر نشدند بلکه با سطحی از واقعیت به نام واقعیت کوانتومی آشنا شدیم که درک و فهم متعارفی را به چالش کشید تا جایی که نظریه کوانتوم پیچیده ترین و غیر قابل فهم ترین نظریه علمی تا به امروز شده است.

پیچیدگی البته موضوعی است که قدمتی به اندازه خود دانش جدید دارد. نیوتون برای اولین بار متوجه شد که سیستم قانون مندی که کشف کرد و مکانیک سماوی و مکانیک زمینی گذشتگان را با دقت باور نکردنی در یک چارچوب و به زیبایی توصیف می کند، بر لبه های تیزی حرکت میکند. لبه ای که هر گونه تغییر در آن منجر به آشوب و پیش بینی ناپذیری می شود. مساله سه جسم یک مثال معروف آن است. وقتی سه جسم تقریبا هم وزن را بخواهید با معادلات دیفرانیسل نیوتون توصیف کنید پیش بینی ناپذیری که جزیی از پیچیدگی است وارد می شود!

اما علاوه به موانع بر سر فهم چنین نظریه هایی (که هنوز چیزهای زیادی از آن را نمی دانیم) دانشمندان متوجه سیستم های بسیار ساده ساختگی(artificial) شدند که باز هم قادر به تولید پیچیدگی هستند. منظور از ساختگی این است که این سیستم ها قابل برنامه نویسی در یک کامپیوتر هستند(برخلاف نظریه کوانتوم) و ظاهرا همه چیز آن ها ساده است ولی رفتار های پیچیده از خود نشان می دهند! جان کانوی و استفن ولفرام اشخاصی بودند که علاقه مند به مطالعه این سیستم ها شدند. در دهه هشتاد میلادی ولفرام علاقه زیادی به درک شبکه های عصبی داشت اما او به دنبال مدل های حتی ساده تری بود. به همین خاطر اتوماتای سلولی(cellular automata) را اختراع کرد. اتومات سلولی شبیه به یک بازی بسیار ساده مانند تخته نرد است. شما یک ردیف از خانه ها دارید و هر خانه یا می تواند خالی(0) یا پر(1) باشد. مثلا یک حالت می تواند به صورت زیر باشد.

حالا می خواهیم مهره ها(1ها) را جابجا کنیم. قاعدتا نیاز به قانون داریم. فرض کنید وضعیت هر خانه را دو سلول کنار آن یعنی همسایه های آن تعیین کنند. به عبارتی خالی یا پر بودن هر خانه تابعی از دو خانه سمت راست و چپ آن است.

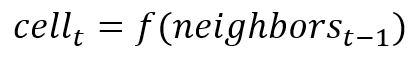
این یعنی وضعیت سلول در زمان t توسط وضعیت سلول های همسایه در زمان قبلی یعنی t-1 تعیین می شود.(زمان یعنی انجام هر حرکت در این بازی). در اصطلاح اتومات های سلولی ما از یک نسل به نسل بعد می رویم. یعنی هر قدم یک نسل جدید بر اساس نسل قبلی ایجاد می کند.

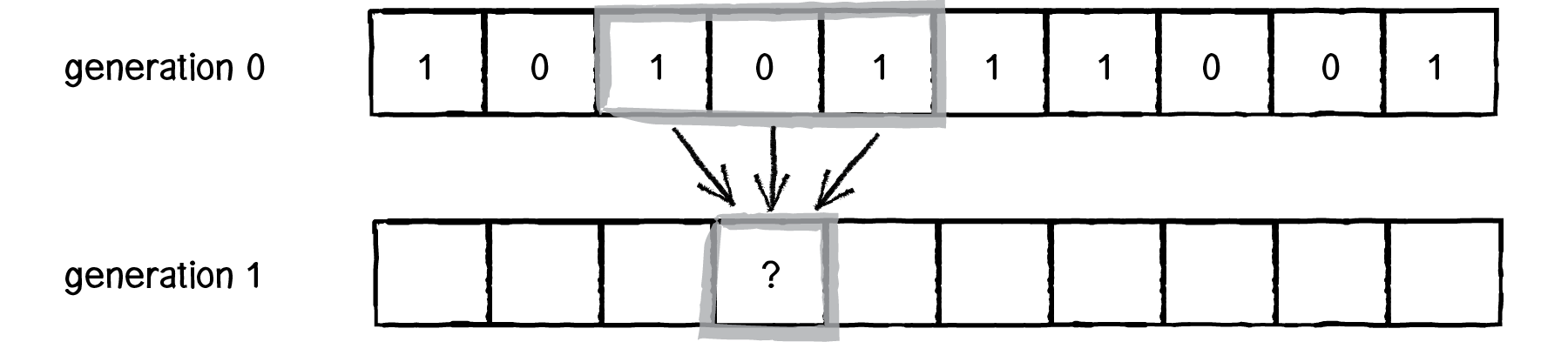
اگر اینطور باشد کلا هشت حالت برای تصمیم گیری داریم. یعنی هر سه خانه در نهایت می توانند هشت حالت ممکن داشته باشند.(از 000 تا 111). یک قاعده را می توان به صورت زیر تصور کرد.

در این قاعده مثلا اگر خانه وسطی شما یک است و دو خانه کناری هم یک، در نسل بعدی به جای آن خانه (وسطی) صفر می گذاریم. یا اگر خانه وسط یک است و خانه راست صفر و خانه چپ یک نسل بعدی یک می شود و به همین ترتیب. بنابراین کافی است این پنجره سه تایی را از چپ به راست(یا برعکس) بلغزانیم و هر ترکیبی که دیدیم به قاعده هایمان رجوع کنیم و انتخاب کنیم. مثلا برای مورد زیر پنجره بر روی 010 است با مراجعه به قاعده ها می بینیم که باید نسل بعدی را 0 بگذاریم و این کار را می کنیم!

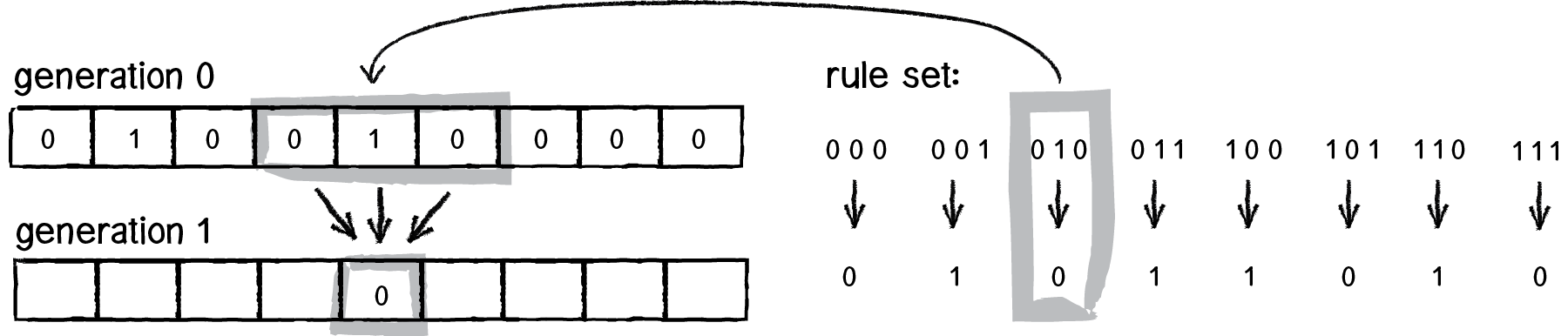
چیزی که در بالا می بینید یک قاعده دلبخواهی هست و هیچ دلیلی هم برای آن وجود ندارد. شما می توانید قاعده را هر طور که بخواهید عوض کنید. مثلا قاعده 30 به صورت زیر اتفاق می افتد:

اما در کل چند قاعده می توانیم داشته باشیم؟ باز هم تمام ترکیب های ممکن صفر و یک برای هشت حالت بالا که می شود(2^8=256) حالت! به این ترتیب می توانیم 256 قاعده بازی داشته باشیم و به هر کدام شماره ای بدهیم. اگر برای شماره گذاری از صفر شروع کنیم از قانون صفر تا 255 خواهیم داشت. مثلا قاعده مثال اول 01011010 است پس عدد آن 90 است(قاعده 90). ولفرام شروع به مطالعه این سیستم های بسیار ساده کرد. برای همین او تمام قواعد را ردیف کرد و سیر تحول آن ها را بررسی کرد. برای این کار او ردیف نسل ها را از بالا به پایین روی هم چید تا ببینید آیا الگویی دارند یا خیر. برای این کار او به جای صفر و یک از خانه های پر(1) و خالی(0) استفاده کرد. مثلا قاعده بالا به شکل زیر در می آید:

او از یک خانه پر در مرکز و بقیه خانه ها خالی به عنوان نسل اول استفاده کرد.

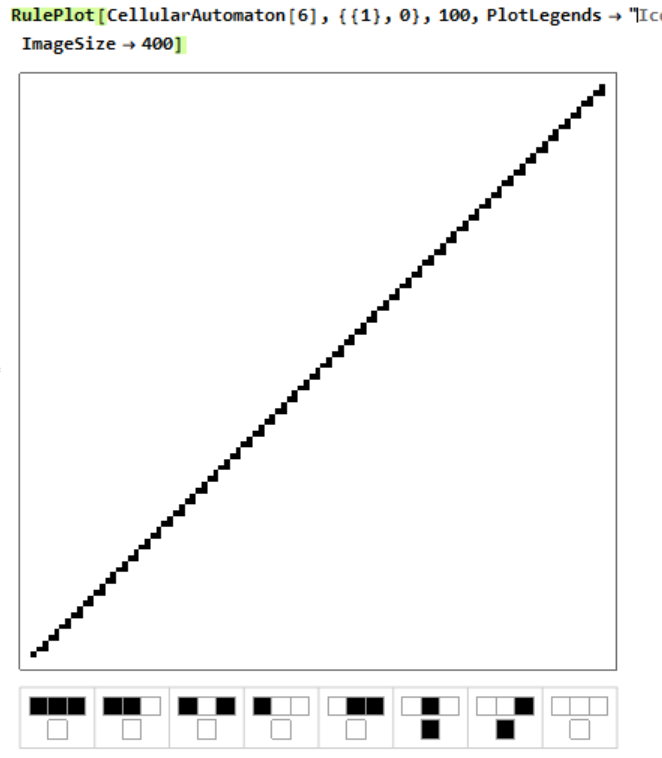
سپس قواعد را اعمال کرد. نتایج برای بیشتر قواعد همانطور که انتظار می رفت ساده بود. یعنی الگوهایی که ایجاد می شدند بسیار ساده و یا تکرار شونده بودند. مثلا rule 0 را در نظر بگیرید. این قاعده می گوید همه خانه ها باید صفر(خالی) شوند پس نتیجه بعد از یک نسل صفر می شود و همه خانه ها بعد از آن خالی اند. اما برخی از قواعد الگوهای تکرار شونده ای مثل مورد زیر(قاعده 6) را ایجاد می کنند.

برخی مانند قاعده 90(که در بالا به عنوان اولین مثال بررسی کردیم)شکل های جالب تری مانند یک فراکتال را تولید می کنند:

اگر چه این شکل بسیار جالب تر است و نشان از پیچیدگی بیشتری است اما همچنان قاعده مند و ساده است. می توانید آن را با یک فرمول بازگشتی ساده هم بنویسید(مثلث خیام در کتاب هندسه دبیرستان). اما برای چند قاعده سطح پیچیدگی بسیار بالاتر می رود. ولفرام برای اولین بار با دیدن این نمونه ها مانند هر کس دیگری دچار شگفتی شد. این الگوها بسیار تصادفی، پیچیده و بدون هیچ گونه الگوی تکرار شونده بودند. قاعده 30 یک نمونه آن است:

تصور ظهور این سطح از پیچیدگی و بی نظمی از یک قاعده ساده ناممکن به نظر می رسد. نکته جالب ماجرا این است که هیچ راهی برای فروکاهش این پیچیدگی به اجزای سازنده اش وجود ندارد. قاعده 30 یک اتم پیچیدگی در دنیای ماست! پیچیدگی ای غیرقابل کاهش! اگر شما ردیف ها را ادامه بدهید هرگز به تناوب نمی رسید و قاعده با جلو رفتن الگوهای تازه و تازه تری برای شما خلق می کند! ولفرام از لحاظ دیداری این موضوع را حدس زد اما بعدها Devaney و Kudson ثابت کردند[3] که قاعده 30 بر اساس تعریف های دقیق تر ریاضی هم دارای رفتار پیچیده و آشوبناک است! به طور مثال این قاعده به شرایط اولیه حساس است. اگر نسل اول را کمی تغییر دهید نتایج کاملا متفاوت خواهند شد(اثر پروانه ای!).

قواعد دیگری هم وجود دارند که رفتارهای پیچیده و کاملا متفاوتی از خود نشان می دهند مانند قاعده 90، 110 و 184. در طبیعت هم می توان نمونه هایی از این الگو ها را دید. معروف ترین آن ها یک صدف دریایی به اسم conus textile است.

قاعده 30 آنقدر رفتار نامنظم و پیش بینی ناپذیری دارد که در بسته نرم افزاری mathematica برای تولید اعداد تصادفی از آن استفاده می شود.

برای قاعده 110 ثابت شده است که این قاعده از لحاظ محاسباتی جهانی (universal) است یعنی می توان از آن به عنوان یک ماشین تورینگ استفاده کرد یا به زبان ساده تر این قواعد برای ساخت یک کامپیوتر کامل برای انجام هر گونه عملیات محاسباتی کافی هستند! آن ها می توانند جمع و ضرب و تفریق انجام دهند و اگر سیستمی بتواند چنین کاری کند هر کار محاسباتی دیگری را هم می تواند انجام دهد! این یافته، تز "جهان به عنوان یک کامپیوتر" را هم تقویت می کند. به عبارتی برای داشتن یک سیستم محاسباتی کامل نیازی به تنظیمات بسیار دقیق برای ایجاد آن نداریم. چنین ماشین هایی آنقدر ساده هستند که براحتی به صورت تصادفی هم ایجاد می شوند!!(احتمال ایجاد قاعده 30 فقط یک در 256 است که عدد بسیار بزرگی است!) و وقتی ایجاد شدند می توانند در قالب سیستم های حیات به بقای خود ادامه دهند و فرم های پیچیده تر و پیچیده تری هم ایجاد کنند!

به طور خلاصه می توان گفت علم پیچیدگی در سر آغاز خود قرار دارد. سیستم های زیادی وجود دارد که نیاز به مطالعه دقیق تر دارند. اما چیزی که مشخص است این است که:

پیش فرض های قدیم در مورد روش علمی دیگر اعتبار چندانی ندارند. پیچیدگی همیشه قابل فروکاهش نیست و پیچیدگی لزوما نیاز به تنظیمات دقیق یا خالق ندارد. پیچیدگی در قلب طبیعت در ساده ترین پیکربندی های طبیعی خود ایجاد می کند و برای بقای خود می جنگد. اتم های پیچیدگی همه جا هستند!

دفعه بعدی که از پنجره اتاق به حرکت پرنده ها و طبیعت یا حتی رفتار آدم ها در خیابان نگاه کردید دیدگاه دیگری به پیچیدگی آن ها دارید!

منابع:

[1] Manukyan, L., Montandon, S. A., Fofonjka, A., Smirnov, S., & Milinkovitch, M. C. (2017). A living mesoscopic cellular automaton made of skin scales. Nature, 544(7649), 173.

[2] Shiffman, D. (2012). The Nature of Code: Simulating Natural Systems with Processing. Daniel Shiffman.

[3] Cook, M. (2004). Universality in elementary cellular automata. Complex systems, 15(1), 1-40.