برای ارزیابی الگوریتمهای یادگیری ماشین، روشهای متنوعی وجود دارد و هر کدام از دیدگاههای مختلفی، درستیِ نتایجِ الگوریتمها را بررسی میکنند. در پست قبلی دربارهی تفاوت Precision و Recall صحبت کردم. این بار به سراغ دو مفهوم sensitivity و specificity رفتم و در انتها دربارهی منحنی Receiver Operating Characteristic یا ROC توضیح خواهم داد. اگر تازه وارد حوزهی یادگیری ماشین شدهاید و میخواهید دربارهی ارزیابی طبقهبندها بیشتر بدانید، پیشنهاد میکنم ابتدا پست مربوط به Precision و Recall را مطالعه کرده و سپس ادامهی مطلب را بخوانید.
یادآوری
تعریف True Positive یا TP: ورودی برچسب یک دارد و الگوریتم نیز به درستی (True) برچسب یک (Positive) را تشخیص داده است.
تعریف True Negative یا TN: ورودی برچسب صفر دارد و الگوریتم نیز به درستی (True) برچسب صفر (Negative) را تشخیص داده است.
تعریف False Positive یا FP: ورودی برچسب صفر دارد و الگوریتم به اشتباه (False) برچسب یک (Positive) را تشخیص داده است.
تعریف False Negative یا FN: ورودی برچسب یک دارد و الگوریتم به اشتباه (False) برچسب صفر (Negative) را تشخیص داده است.
هنگامی که بخواهیم عملکرد یک طبقهبند را در یک کلاس بر اساس Sensitivity بررسی کنیم، تمرکزمان روی تعداد مواردی است که برچسب آن کلاس به درستی تشخیص داده شده است. در یک طبقهبند دو کلاسه، میزان Sensitivity نشان میدهد که الگوریتم چند درصد از مواقعی که برچسب واقعی ۱ بوده ، درست تشخیص داده است.
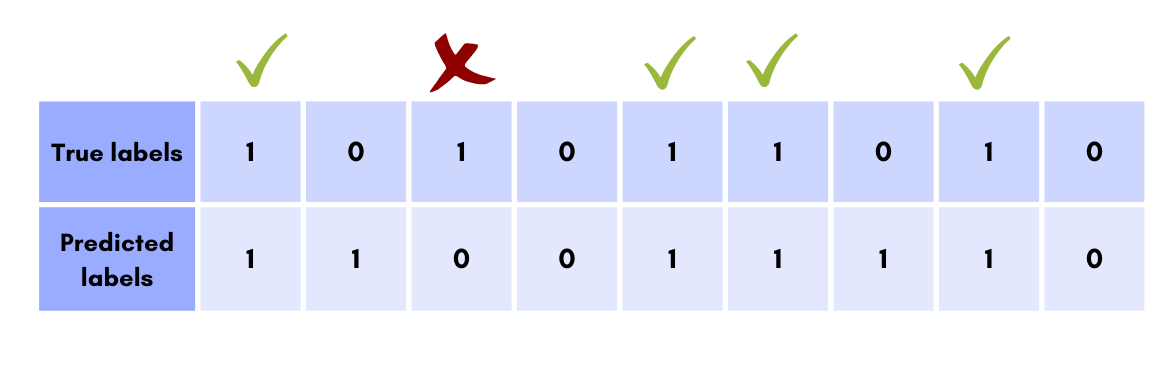
در این مثال از بین ۵ نمونه که برچسب واقعی آنها ۱ است، ۴ مورد درست تشخیص داده شده و بنابراین میزان Sensitivity برابر است با 4/5 یا ۸۰٪ .
اگر دقت کنید این همان معیار Recall است. در واقع Sensitivity نام دیگر Recall بوده و فرمول آن به صورت زیر است:
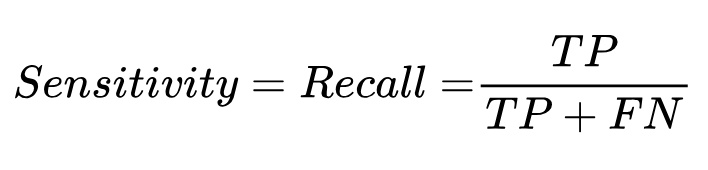
در ارزیابی طبقهبندی یک الگوریتم، معیار Specificity در مقابل Sensitivity قرار دارد؛ از این جهت که بررسی میکند چند مورد از دادههای با برچسب ۰ واقعی درست تشخیص داده شده است:
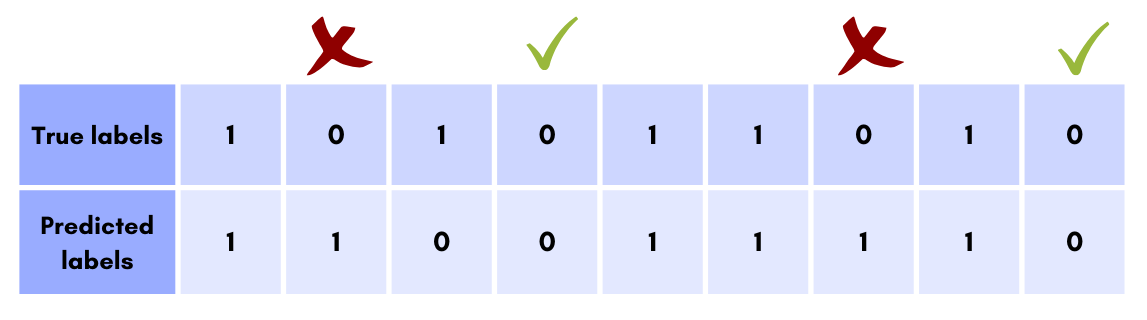
در این حالت، از بین ۴ مورد که برچسب واقعی آنها ۰ بوده، دو مورد درست تشخیص داده شده و بنابراین میزان Specificity برابر با ۵۰٪ است.
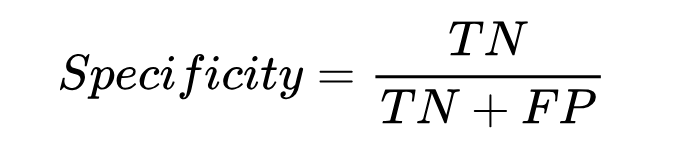
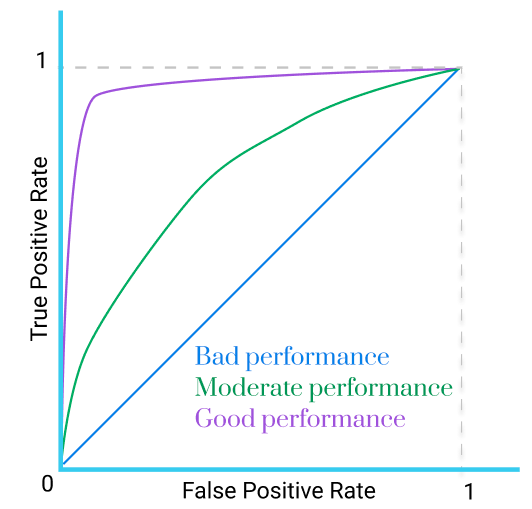
برای مقایسهی عملکرد الگوریتمها روی یک مجموع داده، میتوان یک منحنی رسم کرد که محور افقی نشاندهندهی نرخ False positive یا همان 1 منهای Specificity (متمم) و محور عمودی نیز نشاندهندهی نرخ True positive یا همان Sensitivity باشد. به این منحنی Receiver Operating Characteristic یا ROC گویند.
این منحنی را میتوان برای ارزیابی الگوریتمهایی که خروجی آنها یک مقدار احتمالاتی است استفاده کرد؛ مانند الگوریتمهای logistic regression ، SVM و شبکههای عصبی. برای الگوریتمهایی که خروجی آنها به طور مستقیم برچسب دادههاست (مانند درخت تصمیم و knn) با اندکی تغییرات میتوان نمودار ROC کشید. همچنین این روش ارزیابی برای مسائل باینری (دو کلاسه) مناسب است.
برای هر الگوریتمی که بخواهیم این منحنی را رسم کنیم، کافی است حالتهای مختلف به ازای threshold ها یا Hyperparameter های متفاوت (بسته به نوع الگوریتم) را در نظر بگیریم و مقادیر Sensitivity و Specificity را محاسبه کنیم. آنگاه نمودار ROC را رسم کنیم.
برای نمونه مسئلهی سادهای را در نظر بگیرید؛ فرض کنید میخواهیم از روی شاخص خون افراد، تشخیص دهیم که شخص سالم است یا مبتلا به سرطان.
پس در اینجا فقط یک ویژگی داریم که همان شاخص خون افراد است و دادهها در یک بُعد قرار میگیرند. فرض کنید که ورودیها ۱۰ تا هستند. برای تعیین مرز جداکننده، میتوان threshold های مختلفی انتخاب کرد. اگر میزان این آستانه برابر ۴۰ باشد، مجموعهدادهها به این صورت جدا میشوند:
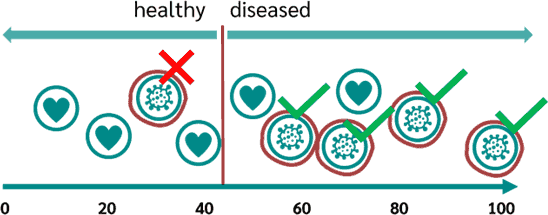
در تصویر بالا، خط جداکنندهی قرمز نشان میدهد که هر دادهای که سمت چپ آن باشد برچسب آن سالم است و در غیر این صورت بیمار. به عبارت دیگر، هر فردی که شاخص خونش از ۴۰ کمتر باشد سالم بوده و بیش از ۴۰ نشاندهندهی ابتلای او به سرطان است.
همانطور که در تصویر مشاهده میشود، با انتخاب آستانهی ۴۰ میتوان از بین ۵ بیمار، ۴ مورد را درست تشخیص داد. پس میزان Sensitivity برابر با ۵÷۴ است یعنی ۰٫۸. برای محاسبهی Specificity با توجه به تصویر بالا، از بین ۵ فرد سالم، سه نفر درست تشخیص داده شده است: ۵÷۳ یعنی ۰٫۶ و اگر ۱ منهای Specificity را در نظر بگیریم، نرخ False positive برابر با ۰٫۴. علت این که متمم Specificity محاسبه میشود، معنایی است که سطح زیر نمودار ROC نشان میدهد. سطح زیر نمودار یا area under the curve یا AUC شاخص ارزیابی دیگری است که پس از رسم نمودار ROC توضیح خواهم داد.
فرض کنیم میزان آستانه برابر با کمترین مقداری است که با توجه به مقادیر دادهها میتواند باشد:
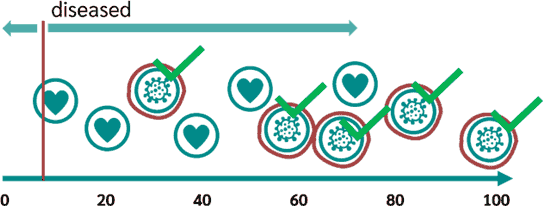
در این حالت همهی موارد بیماری درست تشخیص داده شده و Sensitivity برابر ۱ است. اما همهی موارد سالم به اشتباه بیمار برچسب میخورند. پس Specificity مساوی ۰ است که ما بنا به دلیلی که بیان شد، متمم آن یعنی ۱ را در نظر میگیریم. پس یک مرحله از نمودار ROC به صورت زیر است:
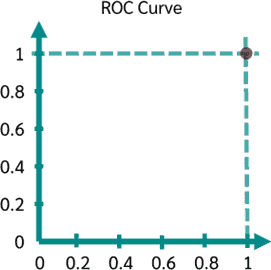
میزان آستانه را به صورت زیر کمی جلوتر میبریم. بدین ترتیب همچنان Sensitivity برابر ۱ است. اما در این حالت از بین ۵ فرد سالم، یک نمونه را درست پیشبینی کردیم. پس میزان ممتم Specificity برابر است با ۰٫۸:
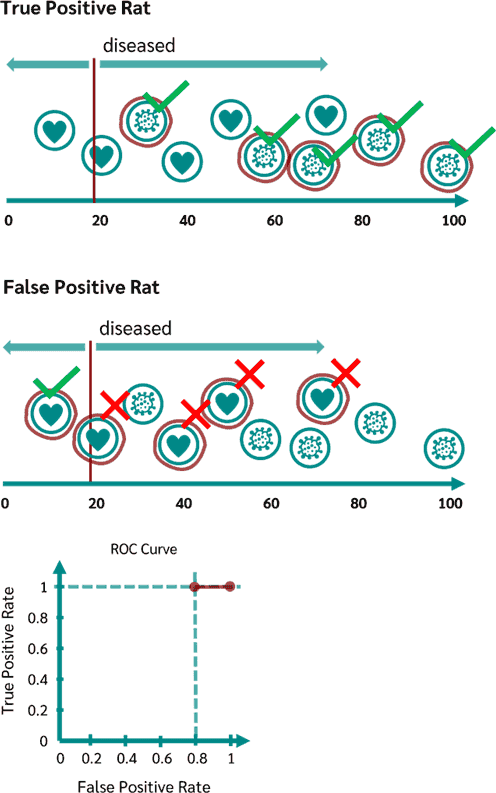
مرحله ۳:
میزان آستانه را جا به جا کرده و روی نمونهی سوم میبریم. بدین ترتیب برای اولین بار Sensitivity کاهش مییاید و به عدد ۰٫۸ میرسد. همچنین متمم Specificity برابر با ۰٫۶ میشود:
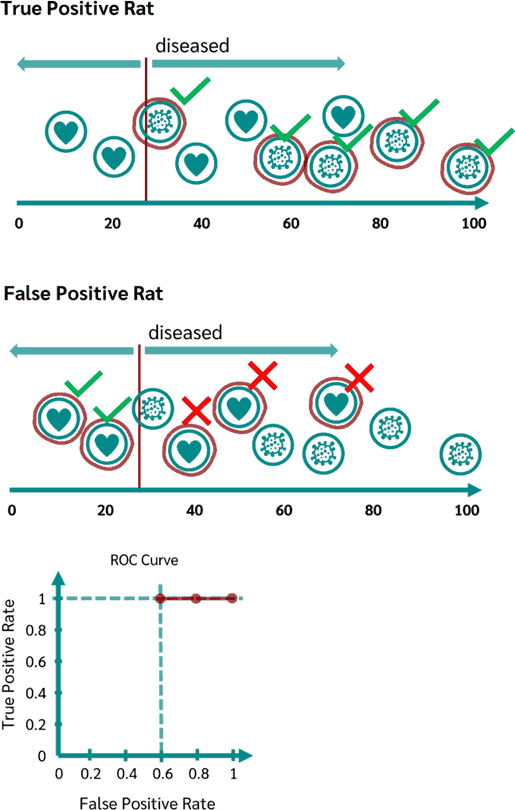
به همین ترتیب برای برای حالتهای دیگر این نمودار را رسم میکنیم تا به شکل زیر برسیم:
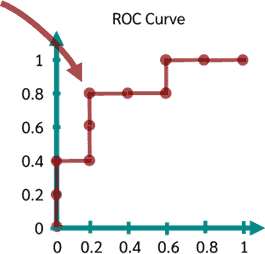
مهمترین ویژگی نمودار ROC این است که میتوان در مقالات از آن به صورت بصری برای مقایسهی یک الگوریتم با سایر الگوریتمهای طبقهبندی استفاده کرد. این کار با در نظر گرفتن سطح زیر نمودار یا AUC -که قبلاً اشاره شد- انجام پذیر است:
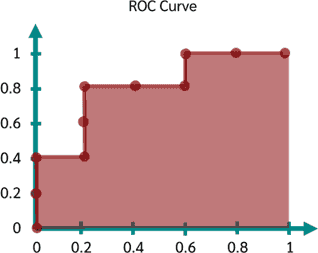
در شکل بالا، سطح زیر نمودار ROC را مشاهده میکنید.
بیشترین مقدار AUC برابر ۱ میتواند باشد. ممکن است در بخش ارزیابی مقالهها مشاهده کنید که در یک دستگاه مختصات، برای مقایسهی چندین الگوریتم متفاوت، چند ROC رسم میشود. هر چه AUC یک الگوریتم بیشتر باشد آن الگوریتم بهتر عمل میکند: