شاید تجربهاش را داشته باشید. زمانی که در فیسبوک یا اینستاگرام دوست تازهای پیدا کرده و او را دنبال میکنید، در کمال ناباوری ببینید تعدادی دوست مشترک، از میان کسانی که فکرش را هم نمیکردید وجود دارند که با دوست جدیدتان دوستند. در واقع دوست تازهی شما تا پیش از این، دوستِ یک یا چند دوستِ شما بوده است و بدون اینکه شما بدانید با او یک ارتباط با یک واسطه داشتهاید که آن را یک ارتباط دوپیوندی مینامیم. این اتفاق ممکن است در یک گروه تلگرامی به ظاهر غریبه هم رخ بدهد که باز هم معنایش همین است. یعنی افرادی در آن گروه هستند که شما از قبل با آنها در ارتباط بودهاید اما خودتان خبر نداشتید.
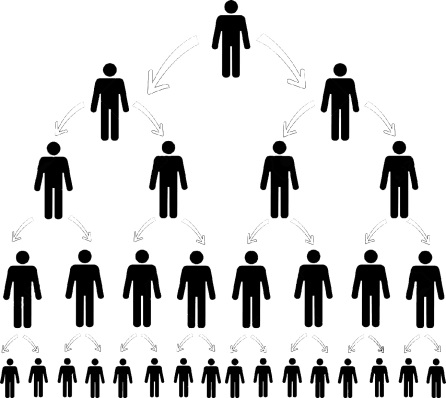
اگر شما صد دوست داشته باشید و هر دوست شما نیز صد دوست داشته باشد که جزو دوستان شما نباشند، شما به واسطه صد دوستتان، دههزار ارتباط دوپیوندی خواهید داشت. دوستانِ دوستانِ شما، با یک واسطه با شما در ارتباط هستند. به همین ترتیب صدها هزار ارتباط سهپیوندی و میلیونها ارتباط چهارپیوندی و دهها و صدها میلیون ارتباط پنجپیوندی نیز دارید. یک چیزی شبیه به آنچه در شکل 1 آمده است. با این حساب و طبق بررسیهای انجام شده، هر شخص برای ارتباط با جمعیت میلیاردی کرهی زمین، به طور متوسط شش پیوند نیاز دارد. یعنی هر نفر روی کرهی زمین که در جامعه بشری حضور فعال دارد به طور متوسط از راه شش نفر به هر شخص دیگری که او هم در جامعه بشری حضور فعال دارد، ارتباط پیدا میکند. گرچه این فرضیه ممکن است برای کسانی که در شبکههای اجتماعی نیستند صدق نکند. البته منظور از شبکه اجتماعی، توییتر، فیسبوک یا اینستاگرام نیست. این را گفتم چون بیشتر ما، واژه «شبکه اجتماعی» را بعد از گسترش ابزارها و فراگیر شدن رسانه های جمعی در فضای مجازی شنیده ایم و به کار می بریم. در حالی که قدمت و مفهوم «شبکه اجتماعی» هم سن و سال زندگی انسان ها و تشکیل جوامع بشری است.
حرفهایی که زدیم فقط برای این نبود که بگوییم مثلا شما، همین الان که دارید این مطلب را میخوانید، از راه تنها پنج نفر، با لئوناردو دیکاپریو -ستاره هالیوود- در ارتباط هستید. چون شاید نیازی به گفتن ما هم نباشد. اگر شما دوستی داشته باشید که با یکی از بازیگران سینمای ایران دوست باشد، آن بازیگر هم با اصغر فرهادی دوست باشد، به واسطه حضور آقای فرهادی در اسکار، ارتباط شما با آقای دیکاپریو به پنج پیوند هم نخواهد رسید.
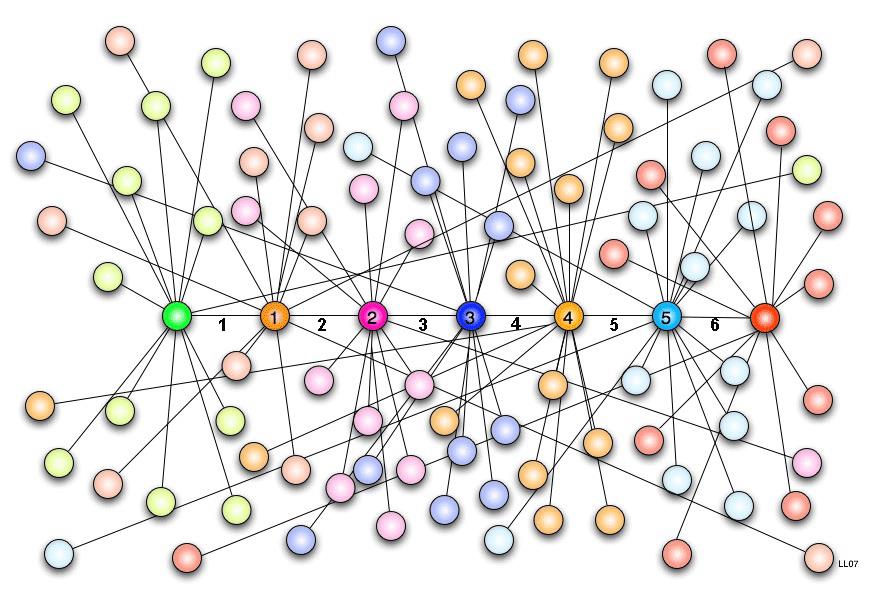
از آنجا که مساله ارتباط در جامعه بشری همیشه هم انقدر ساده نبوده، باعث شده تا دانشمندانی آن را نه تنها بررسی کنند، بلکه برایش فرضیه پردازی هم بکنند تا اهمیت آن را به رخ بکشند. فرضیهای که در نظریه بازیها به «شش درجه جدایی» معروف است و دنیای کوچک اما پیچیده انسانها را بررسی میکند (شکل 2). البته پیش از پیدایش شبکههای اجتماعی مجازی بررسی آن بسیار کار دشواری بود، اما به لطف انقلاب اطلاعاتی که در این سالها شاهدش بودیم، این فرضیه حتی برای افراد عادی بسیار ملموس شده است. گواهش هم این جمله است که این روزها خیلی میشنویم: دنیا خیلی کوچک است.
گفتیم فرضیه «شش درجه جدایی» در نظریه بازیها مطرح شده است. پیش از اینکه به این فرضیه بپردازیم باید اول ببینیم که خود نظریه بازیها چیست و برای چه و از کجا به وجود آمده است.
نظریه بازیها شاخهای جوان از ریاضیات است که به دنبال راهبرد یا استراتژی برای رسیدن به بیشترین منفعت در مسایل گوناگون است. این منفعت ممکن است پول، شهرت، اعتبار و یا هر چیز مادی یا معـنوی دیگری باشد. به تعبیری دیگر نظریه بازیها، ریاضیات رفتار جمعی است.
این نظریه در سدهی گذشته به دلیل گستردگی کاربرد در علوم مرتبط با جامعهی بشری مانند اقتصاد، سیاست، روابط بینالملل و زیستشناسی بسیار پراهمیت شد. از دانشمندان پیشرو و صاحب نام در این شاخه میتوان به جان فون نویمان و جان نش اشاره کرد. تاثیر افرادی مانند جان نش آنقدری بوده که فیلم «ذهن زیبا» را بر اساس زندگینامه او ساختهاند. البته او و همسرش متاسفانه در سال 2015 میلادی بر اثر سانحه رانندگی جان خود را از دست دادند. دانشمندانی مانند نش توانستند با مدلسازی و تحلیل رخدادهای واقعی، جای پای ریاضیات را در جامعه بیش از پیش پررنگ کنند. رویارویی ایالات متحده و شوروی در سالهای جنگ سرد، نمونهای از این رخدادهاست که به عنوان یک بازی با «حاصلجمع صفر» که در آن هر طرف به دنبال حداکثر منفعت است، به کمک این نظریه مدلسازی شد. بازی با حاصل جمع صفر، همان بازی برد-باخت است. همه بازیهایی که در آن برنده شدن یک نفر تنها زمانی رخ میدهد که طرف مقابل ببازد، حاصل جمع صفر هستند. شطرنج از این دسته بازیهاست. اگر در جریان مذاکرات ایران و پنج به علاوه یک بوده باشید، احتمالا باید عبارت توافق برد-برد به گوشتان خورده باشد. مگر مساله هستهای ما و مذاکرات بازی است؟ دلیل این که از واژه برد-برد برای این توافق استفاده میشود، همین نظریه بازیها و تاثیراتش در علوم ارتباطات بینالمللی است که تیمهای مذاکره کننده آن را بلدند. شاید جالبتر باشد اگر بگویم میشود دلیل محرمانه بودن مذاکرات را هم در نظریه بازیها یافت. مدلی به نام جزیره پرندگان در این نظریه وجود دارد که پرداختن به آن نیازمند فرصت بیشتری است، اما در این مدلسازی مساله وجود تماشاچی در میان دو پرنده که در حال مجادله یا مذاکره(!) بر سر غذا هستند بررسی شده است. بر اساس نقش تماشاچی در این جزیره پرندگان میتوان استنباط کرد که چرا مذاکرهکنندگان بر محرمانه بودن مذاکره تا رسیدن به نتیجه نهایی، تاکید داشتند.

به جز دستهبندی حاصلجمع صفر-حاصلجمع غیرصفر، بازیها را میتوان از دیدگاههای دیگری مانند متقارن–نامتقارن، تصادفی-غیرتصادفی و باآگاهی کامل-بدون آگاهی کامل بخشبندی کرد. برای نمونه، شطرنج یک بازی غیرتصادفی با آگاهی کامل و حاصلجمع صفر است. چرا که شانس در آن نقش ندارد، هر دو طرف چینش همهی مهرهها را میبینند و نسبت به شرایط بازی آگاهی کامل دارند و همچنین به طور همزمان، هر دو طرف نمیتوانند برنده باشند. با این تعریف منچ یک بازی نیمه تصادفی است، چون اینکه کدام مهره حرکت کند با شماست، اما اینکه چند خانه حرکت کند را تاس و در واقع شانس مشخص میکند.

حالا که چند کاربرد از نظریه بازیها را دیدیم، بهتر است به بحث اولمان برگردیم. گفتیم یکی از موارد بررسی شده در نظریهی بازیها ارتباط میان افراد در جامعه بوده است. که فرضیهی «شش درجه جدایی» و همچنین «دنیای کوچک» به بخشی از آن پرداختهاند و به صورت تجربی نشان دادهاند که زنجیرهای میان انسانها وجود دارد که همزمان با داشتن پیچیدگی بالا ویژگی شگفتانگیزی دارد که آن فاصلهی ناچیزِ میان هر دو حلقهی این زنجیر است. بنابر آزمایشها و بررسیهای انجام شده این عدد، نزدیک به 6 است، یکی از افراد مشهوری که در سال 1990 توسط سه دانشجوی کالج آلبرایت در آمریکا مورد بررسی قرار گرفت کِوین بِیکِن، بازیگر مشهور هالیوود بود که به خاطر شمار بالای فیلمهایی که بازی کرده بود و همچنین تنوع همبازیهایش در هر فیلم نمونهی مناسبی برای آزمایش و بررسی بود.
دانشجویانی از دانشگاه ویرجینیا علاقهمند به این موضوع شده و نموداری از بازیگران هالیوود (که تنها بخش کوچکی از آنها با بیکن همبازی بودند) آماده کردند، بیکن در مرکز آن نمودار قرار داشت. سپس ارتباط میان بیکن و دیگر بازیگران را از نظر طول زنجیرهی انسانی بررسی کردند و به نتایج زیر رسیدند:
1592 بازیگر به صورت مستقیم با بیکن، در فیلمهای گوناگون همبازی بودند.
169274 نفر با دو پیوند به بیکن میرسیدند.
بیش از 470000 نفر با سه پیوند به بیکن میرسیدند.
به طور میانگین بیکن با 770269 نفر از بازیگران هالیوود نزدیک به سه پیوند فاصله داشت. این در حالی بود که فاصلهی بیکن با 770187 نفر از بازیگرانی که در این نمودار نبودند نزدیک شش پیوند بود.
در واقع بزرگترین عدد که به معنای بیشترین فاصله بود برابر با 6 به دست آمد، که مهر تاییدی بر فرضیهی شش درجه جدایی در آن زمان بود.
البته بررسیها و آزمایشهایی مانند این، تنها به اینجا ختم نشد. هنوز هم در دنیا دانشمندان بسیاری در حال کار بر روی نظریه بازیها و گسترش کاربردهای آن هستند.
از امروز با دانستن این موضوع، و شناخت نسبی از نظریه بازیها، بیش از اینکه از دیدن دوستان مشترک در جاهایی که فکرش را نمیکنیم، تعجب کنیم، میتوانیم مسایل شگفتانگیز و روزمره دیگری که در زندگیمان هست را از زاویه دیگری ببینیم. یک زاویه علمی و منسجم! شاید ما هم به فرضیهای نو برسیم. اگر هم نرسیدیم مهم نیست. مهم این است که بدانیم خیلی چیزها که در زندگی روزمرهمان داریم، مانند مهارت ارتباط اجتماعی پایههای علمی هم دارد.