یادگیری ماشین به زبان من ( مرحله 6 - رگرسیون , Regression)

رگرسیون (Regression) یعنی پیدا کردن یه رابطه‌ی ریاضی بین چند تا عدد که کمکمون می‌کنه یه چیز ناشناخته رو پیش‌بینی کنیم.

فرض کن می‌خوای بدونی قد بچه‌ها بر اساس سن‌شون چطوری تغییر می‌کنه.

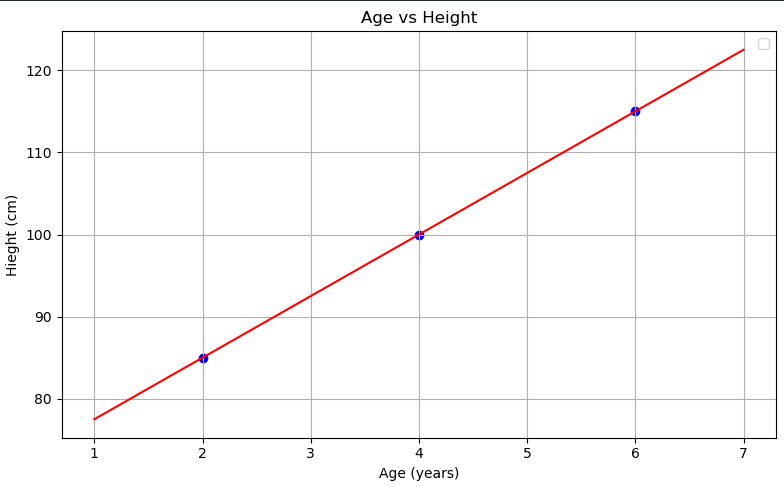
کد کامل :

import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression

X = np.array([[2], [4], [6]])
y = np.array([85, 100, 115])

model = LinearRegression()
model.fit(X, y)

x_range = np.linspace(1, 7, 100).reshape(-1, 1)
y_pred = model.predict(x_range)

plt.figure(figsize=(8, 5))
plt.scatter(X, y, color='blue')
plt.plot(x_range, y_pred, color='red')
plt.title('Age vs Height')
plt.xlabel('Age (years)')
plt.ylabel('Hieght (cm)')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()

حالا این به چه دردی میخوره ؟ الان میتونیم پیش بینی کنیم مثلا:

model.predict([[2]]) # 85.0

یعنی اگه یه نفر ۲ سالش باشه، مدل پیش‌بینی می‌کنه که قدش حدود ۸۵ هست .
و خب... تبریک می‌گم! 🎉
شما الان یک مدل ساده‌ی هوش مصنوعی ساختید که می‌تونه پیش‌بینی انجام بده!

این رگرسیون یک رگرسیون بسیار ساده بود , همیشه مسائل انقدر ساده نیستن و این نوع رگرسیون حلال همه مشکلات ما نیست , در ادامه به صورت کامل تر در مورد رگرسیون و بهبود رگرسیون صحبت میکنیم

چطوری بفهمیم رگرسیونمون داره درست کار میکنه یا خیر ؟

سه تا فرمول اصلی وجود داره برای اینکه تست کنیم آیا پیش بینی های رگرسیونمون درسته یا خیر :

۱- میانگین خطای قدر مطلق MAE (Mean Absolute Error)

۲- میانگین مربعات خطا (MSE (Mean Squared Error

۳- ریشه RMSE (Root Mean Squared Error)

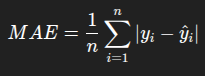
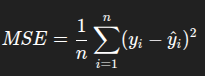
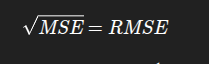
کدش هم بسیار ساده هستش :

from sklearn.metrics import mean_absolute_error, mean_squared_error
import numpy as np
y_true = [100, 150, 200, 250]
y_pred = [110, 140, 195, 260]
mae = mean_absolute_error(y_true, y_pred)
mse = mean_squared_error(y_true, y_pred)
rmse = np.sqrt(mse)
print("MAE:", mae)
print("MSE:", mse)
print("RMSE:", rmse)

خروجی کد :

MAE: 7.5 (به‌طور میانگین، مدل ۷.۵ واحد خطا داشته)
MSE: 62.5 (مربع خطاهاست؛ خطاهای بزرگ رو بیشتر جریمه می‌کنه)
RMSE: 7.905694150420948 (مثل MAE ولی حساس‌تر به خطاهای بزرگ)

خب , ببینید تا به اینجای کار ما فهمیدیم که خطای رگرسیونی که کشیدیم چقدره

اما الان میخوایم یک فرمولی یاد بگیریم که به ما بهینه ترین رگرسیون ممکن رو میده , یعنی انقدر تلاش میکنه تا به بهترین رگرسیون ممکن برسونه ما رو !

گرادیان نزولی یا Gradient Decent

یک الگوریتم آموزش برای پیدا کردن بهترین پارامترها (مثلاً a و b در معادله خط):

با استفاده از مشتق متریک خطا (مثل MSE)، مشخص می‌کنه چجوری وزن‌ها رو تغییر بده تا خطا کم بشه.

که در پست بعدی کامل در موردش توضیح دادیم

واحد های حرفه ای بررسی رگرسیون :

ببینید ما الان باید بتونیم تشخیص بدیم دقت مدلمون (رگرسیون) چقدره . یعنی باید خط رگرسیون رو رسم کنیم , یک خط پیش بینی هم رسم کنیم . بعد ببینیم رگرسیونمون به پیش بینی چه نسبتی داره .

اگر خط رگرسیون چطوری کشیده شده باشه خوبه یا بده :

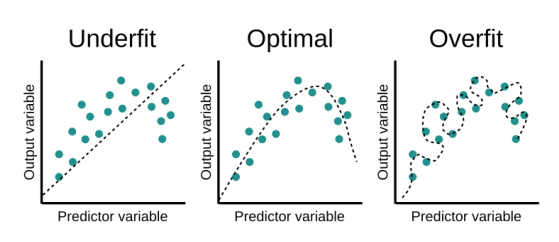
حالا باید ببینیم ما رگرسیونمون خوبه یا بد :

اگر Overfit باشه (حفظ کرده)

این یعنی که مدل ما دقیقا مثل کسی هستش که فقط تونسته جزوه رو حفظ بکنه یعنی نیومده درسش رو خونده باشه درک کرده باشه و وقتی ازش سوال بپرسیم بتونه با درک خودش جواب بده . فقط میتونه سوالای تو جزوه رو جواب بده

اگر Underfit باشه (نه حفظ کرده نه یاد گرفته)

یعنی نه میتونه بر اساس چیزایی که تو جزوه یاد گرفته جواب بده نه بر اساس منطق خودش از درک درس . و این بدترین نتیجه ممکنه .

اگر Optimal باشه ( یعنی هم یاد گرفته و هم حفظ کرده)

این حالت چیزی هستش که میخوایم .

حالا ما چطوری بفهمیم رگرسیونی که کشیدیم underfit شده یا overfit یا optimal ?

مثال با MSE :

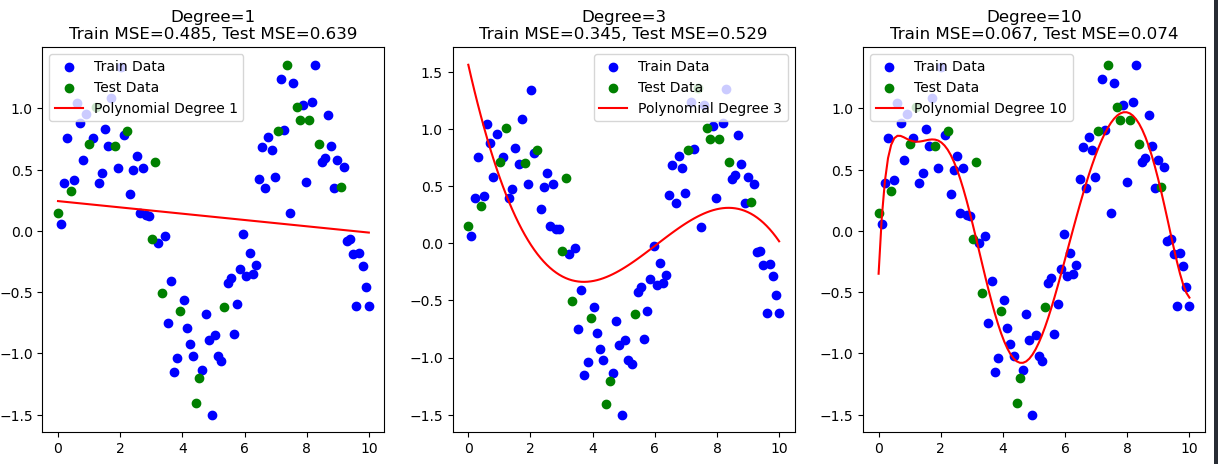
الان دقت کنید :

ما یک مدل Train رو دادیم به سیستم و براش رگرسیون رسم کردیم (جزوه ای که دانش آموز خونده)

و داریم با Test مقایسه میکنیم (سوالی که ازش میپرسیم)

نتیجه چطور شده :

• Degree 1 (رگرسیون خطی ساده):
  Train MSE = 0.485, Test MSE = 0.639
  خطا روی داده آموزش و تست نسبتاً بالا و نزدیک به هم هست؛ یعنی مدل ساده است و نمی‌تواند الگوهای پیچیده را خوب یاد بگیرد.

• Degree 3 (رگرسیون چندجمله‌ای درجه ۳):
  Train MSE = 0.345, Test MSE = 0.529
  خطاها نسبت به مدل ساده‌تر کمتر شده‌اند و مدل بهتر توانسته پیچیدگی داده را یاد بگیرد؛
  اما هنوز خطای تست کمی بیشتر از خطای آموزش است که طبیعی است.

• Degree 10 (رگرسیون چندجمله‌ای درجه ۱۰):
  Train MSE = 0.067, Test MSE = 0.074
  خطای آموزش خیلی پایین است (یعنی مدل دقیقاً داده آموزش را یاد گرفته)
  و خطای تست هم نسبتاً پایین و نزدیک به خطای آموزش است.
  این یعنی مدل پیچیده است ولی توانسته تعمیم خوبی هم به داده‌های جدید بدهد، پس Overfitting شدید مشاهده نمی‌شود.

حالا چرا با MSE نتیجه رو بررسی کردیم ؟ ما که RMSE هم داشتیم .

اولا که جدای فرمول هایی که تا الان بهتون گفتم برای بررسی خطای رگرسیون ما ۳ فرمول دیگه هم داریم که ,

R-sqared , Adjusted R-Squared

نام دارند و در ادامه در مورد اینکه کدوم یک بهتر هستند برای بررسی نتیجه صحبت خواهیم کرد .

ابتدا کد رو ببینید :

def print_metrics(y_true, y_pred, n_features, dataset_name):
        ssres, mse, rmse, r2, adj_r2 = model_metrics(y_true, y_pred, n_features)
        print(f"{dataset_name}:")
        print(f"  SSRes: {ssres:.3f}")
        print(f"  MSE: {mse:.3f}")
        print(f"  RMSE: {rmse:.3f}")
        print(f"  R²: {r2:.3f}")
        print(f"  Adjusted R²: {adj_r2:.3f}\n")

print_metrics(y_train, y_train_pred, n_features=2, dataset_name="Train")
print_metrics(y_test, y_test_pred, n_features=2, dataset_name="Test")

نتیجه :

• اگر مدل روی آموزش (Train) : خطاهای خیلی کم و R² خیلی بالا داشته باشه

• اما روی تست (Test) : خطاها زیاد و R² پایین، یعنی Overfit داریم.

• اگر هر دو (آموزش و تست) خطاها بالا و R² پایین باشه، یعنی Underfit داریم.

هایپرپارامتر های رگرسیون

گاهی وقتا توی مدل‌مون کلی ویژگی (feature) داریم، بعضیاشون هم خیلی به درد بخور نیستن. اگه بخوایم با همه‌شون مدل بسازیم، ممکنه مدل‌مون دچار overfitting بشه (یعنی زیادی خودش رو با داده‌های آموزش وفق می‌ده و رو داده‌های جدید عملکردش میاد پایین).

اینجاست که Ridge و Lasso میان وسط!

هایپرپارامتر Ridge Regression (ریج)

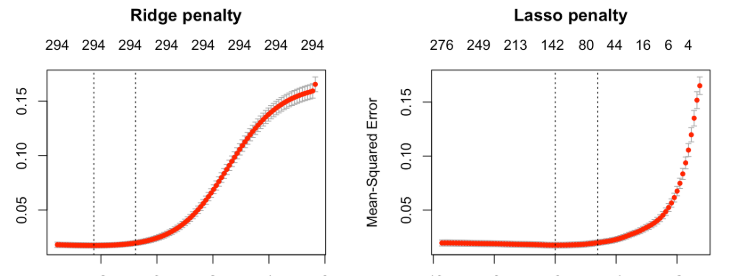
تو Ridge، ما یه جور پنالتی (جریمه) می‌ذاریم روی ضرایب بزرگ. یعنی چی؟ یعنی اگه مدل بخواد یه ضریب بزرگ بده به یه ویژگی، بهش می‌گیم: «نه نه نه! یه کم کوتاه بیا!»

فرمولش :

Loss = MSE + α * (sum of squared coefficients)

هایپرپارامتر Lasso Regression (لاسو)

همچنین Lasso هم پنالتی می‌ذاره، ولی فرقش اینه که به جای توان دوم ضرایب، خودشون رو مستقیم جمع می‌کنه:

Loss = MSE + α * (sum of absolute coefficients)

به پایان این مطلب رسیدیم امیدوارم دوست داشته باشید .

خوشحال میشم نظراتتون رو بدونم .