
الگوریتم Support Vector Machine (ماشین بردار پشتیبان) یا به اختصار SVM از مدل های قدرتمند و همه کارهی ماشین لرنینگ هست. این الگوریتم میتونه برای طبقه بندی های خطی یا غیر خطی، رگرسیون و حتی شناسایی داده های پرت هم استفاده بشه. SVM یکی از محبوب ترین مدل های ماشین لرنینگ هست و یادگیری این الگوریتم برای علاقه مندان ماشین لرنینگ ضروری هست. SVM ها بطور خاص مناسب طبقه بندی دیتاست های با اندازه کوچیک یا متوسط هستند.
توی این مطلب میخوایم با مفاهیم اصلی SVM، طرز استفاده از اونها و کارکرد اونها رو بررسی کنیم.
مفاهیم اصلی پشت SVM رو بهتره با عکس توضیح بدیم.عکسی که پایین میبینید بخشی از دیتاست MNIST هست که تو مطالب قبلی بهش پرداختیم. دو کلاس به راحتی میتونن به وسیله یک خط صاف جدا بشن چون قابلیت جدا شدن بوسیله خط رو دارن (Linearly Separable) شکل سمت چپ نشون دهنده مرز های تصمیمگیری (Decision Boundary) برای سه طبقه بندی خطی هست. مدلی که مرز تصمیم گیری اون بوسیله خط سبز نشون داده شده به قدری بد عمل میکنه که اصلا نتونسته کلاس رو به درستی جدا کنه. دو مدل بعدی روی ترینینگ ست خوب عمل میکنن اما به قدری به نمونه ها نزدیک هستند که احتمالا روی داده های جدید به خوبی عمل نکنند. در مقابل، خط توپر شکل سمت راست نشون دهنده مرز تصمیم گیری یک طبقه بندی SVM هست. این خط نه تنها دسته ها رو جدا میکنه بلکه تا جایی که امکان داره از نمونه های ترینینگ دور هست. میتونید SVM رو اینجوری در نظر بگیرید که بیشترین فضای ممکن بین کلاس ها رو با استفاده از خط های موازی کناری در نظر میگیره. به این روش میگن Large Margin Classification.
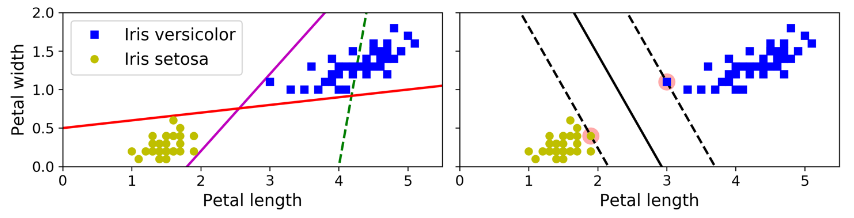
دقت کنید که اضافه کردن نمونه های ترینینگ به خارج از فضای خالی میانی، تاثیری روی مرز های تصمیم گیری نخواهد داشت. در واقع مرز های تصمیم گیری بوسیله نمونه هایی که در بیرونی ترین جای فضای خالی هستند مشخص شده. به عبارت دیگه مرز های تصمیم گیری توسط نمونه هایی که با دایره مشخص شدن پشتیبانی میشن (Supported). به این نمونه ها میگن بردارهای پشتیبان (Support Vectors ).
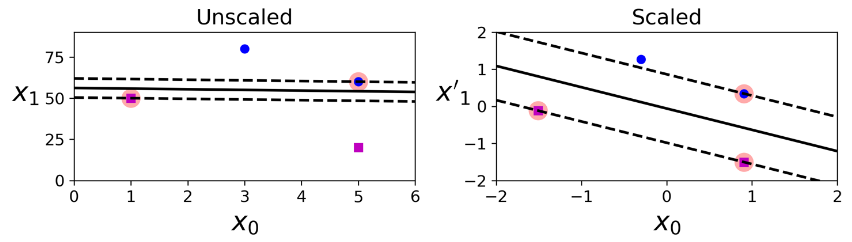
الگوریتم SVM به شدت به مقیاس داده ها حساس هست. همون طور که در شکل سمت چپ میبینید مقیاس عمودی بیشتر از افقی هست بخاطر همین فضای خالی نزدیک به افق هست. بعد از تغییر مقیاس داده ها با استفاده از StandardScaler واقع در کتابخانه Scikit-Learn میبینیم که مرز های تصمیم گیری شکل بهتری پیدا کردن.
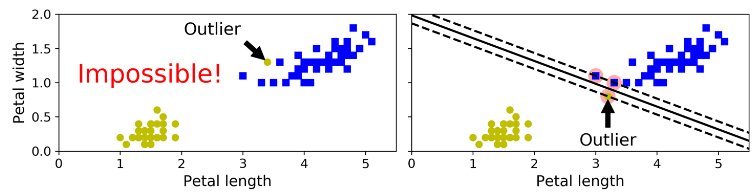
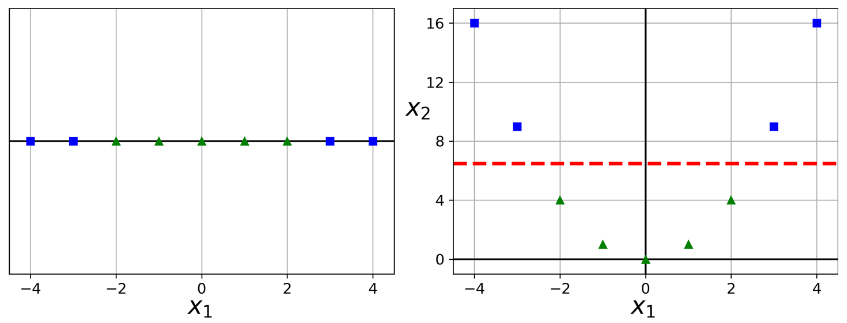
اگه تحمیل کنیم که تمام نمونه ها باید خارج از فضای خالی میانی باشن و حتما باید در سمت مناسب قرار بگیرن، بهش میگن Hard Margin Classification (طبقه بندی حاشیه سخت). این روش دو مشکل اساسی داره.اول اینکه فقط برای دادههایی کار میکنه که بهصورت خطی جدا میشن. دوم اینکه به داده های پرت بهشدت حساس هست. شکلی که پایین میبینید دیتاست Iris رو نشون میده که در سمت چپ یک داده پرت وجود داره و پیدا کردن یک Hard Margin برای اون غیر ممکن هست. در سمت راست هم مرز تصمیمگیری با چیزی که در بالا دیدیم، خیلی فرق داره و احتمالا بهخوبی نمیتونه عمومیسازی کنه.
برای جلوگیری از این مشکلات، از یک مدل انعطاف پذیر تر استفاده میکنیم. هدف ما پیدا کردن یک تعادل مناسب بین بیشترین مقدار فضای خالی میانی و محدود کردن Margin Violations هست (نقض حاشیه یعنی قرار گرفتن نمونه ها در فضای میانی یا در سمت اشتباه) به این کار میگن Soft Margin Classification.
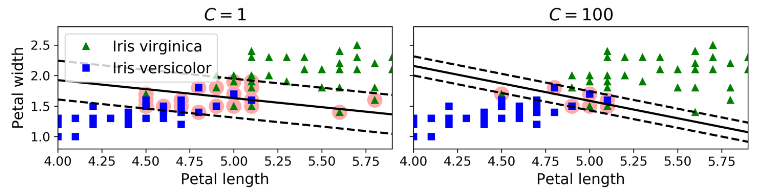
وقتی مدل های SVM رو با استفاده از Scikit-Learn میسازیم، یک سری هایپرپارامتر ها رو میتونیم تنظیم کنیم. یکی از این هایپرپارامتر ها C نام داره. اگر مقدار اون کم باشه، حاصل مدل سمت چپ شکل پایین میشه. با مقدار زیاد به شکل سمت راست میرسیم. نقض حاشیه اتفاق خوبی نیست و بهتره تا جایی که امکان داره، کمتر اتفاق بیفته. اگرچه، در این مورد، درسته که مدل سمت چپ نقض حاشیه های زیادی داره اما احتمالا بهتر عمومیسازی میکنه. در واقع هایپرپارامتر C مقدار مجازات مدل برای هر نمونهای رو که اشتباه طبقه بندی میکنه، تعیین میکنه. هر چقدر C کمتر باشه، حاشیه نرم تر میشه.
اگر مدل شما Overfit شده باشه، میتونید با استفاده از هایپرپارامتر C اون رو Regularize کنید
مقدار C بزرگ: سوگیری کم، واریانس زیاد
مقدار C کوچک: سوگیری زیاد، واریانس کم
کدی که در پایین مشاهده میکنید، دیتاست Iris رو لود میکنه، تغییر مقیاس فیچر ها رو انجام میده و یک مدل Linear SVM رو برای تشخیص گل های Iris Virginica درست میکنه. مدل حاصل رو میتونید در شکل بالا ببینید.
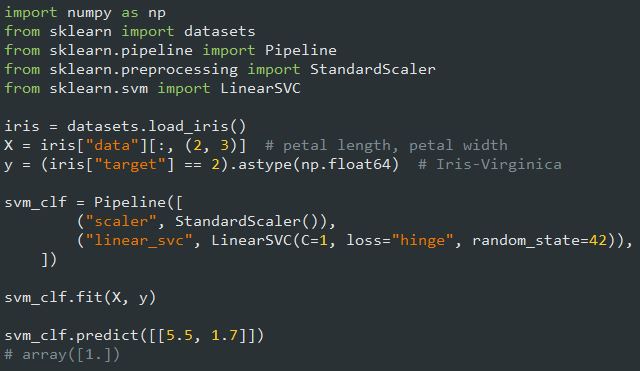
برخلاف Logistic Regression، خروجی مدل های SVM احتمال هر کلاس نیست
بهجای استفاده از کلاس LinearSVC، میتونستیم از کلاس SVC به همراه یک کرنل خطی استفاده کنیم. برای این کار، وقتی میخوایم مدل SVC رو بسازیم، مینویسیم SVC(kernel='linear', C=1). یا میتونیم از کلاس SGDClassifier بهصورت SGDClassifier(loss='hinge', alpha=1/(m*C)) استفاده کنیم. با این روش میتونیم از Stochastic Gradient Descent استفاده کنیم تا یک Linear SVM Classifier درست کنیم. این روش به سرعت کلاس LinearSVC مارو به جواب نمیرسونه اما میتونه کمک کنه تا دیتاست های آنلاین یا دیتاست های بزرگ رو که در حافظه جا نمیشن، بهخوبی مدیریت کنیم.
یکی از تفاوت های LinearSVC با ('SVC(kernel='linear در این هست که اولی از One-Vs-All استفاده میکنه و N * N-1 / 2 تا مدل مختلف درست میکنه (N تعداد کلاس هاست). در حالیکه دومی از One-Vs-One استفاده میکنه و N تا مدل مختلف درست میکنه.
کلاس LinearSVC مقدار خطا رو Regularize میکنه، بههمین سبب باید ترینینگ ست رو با کم کردن مقدار میانگین اون، متمرکز کنید.اگر از StandardScaler برای تغییر مقیاس استفاده کنید، این اتفاق بهطور خودکار رخ میده. همچنین مطمئن باشید که هایپرپارامتر loss برابر hinge هست چون دیفالت اون چیز دیگهای هست. در آخر، برای افزایش بهرهوری، هایپرپارامتر dual رو برابر False قرار بدید، مگر اینکه فیچر ها بیشتر از نمونه های ترینینگ باشن.
گرچه Linear SVM ها کارایی زیادی دارن و در اکثر مواقع هم کار راه انداز هستند، اما خیلی از دیتاست ها اصلا خطی نیستند. یک راه برای مدیریت دیتاست های غیرخطی، اضافه کردن فیچر های بیشتر مثل Polynomial Feature هست. بعضی اوقات این راه جواب میده و به ما یک دیتاست خطی تحویل میده. مثلا شکل سمت چپ رو در نظر بگیرید. یک دیتاست رو با یک فیچر x1 نشون میده. این دیتاست به صورت خطی جداپذیر نیست. اما اگر فیچر دومی به نام x2 که برابر توان دوم x1 هست، اضافه کنید، میشه دیتاست رو با یک خط جدا کرد.
برای پیادهسازی این ایده اول یک Pipeline شامل ترنسفورمر PolynomialFeatures، بههمراه StandardScaler و LinearSVC درست میکنیم. بیاید این رو با دیتاست Moon امتحان کنیم. این دیتاست یک دیتاست تفننی محسوب میشه که برای Binary Classification کاربرد داره.
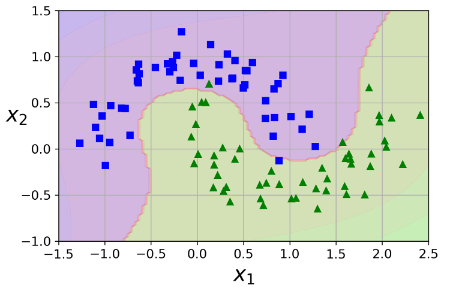
اضافه کردن فیچر های Polynomial کار آسونی هست. این روش نه فقط با SVMها بلکه با تمام الگوریتم های ماشین لرنینگ بهخوبی کار میکنه. چندجملهای های با درجهی کم، نمیتونن با دیتاست های پیچیده کار کنن. چندجملهای های با درجهی بالا، فیچر های زیادی رو تولید میکنن که مدل رو آهسته میکنه.
خوشبختانه وقتی از SVM استفاده میکنید، میتونید از یک تکنیک ریاضی با نام Kernel Trick استفاده کنید. کرنل باعث میشه بدون اضافه کردن Polynomial Feature، همون نتیجهای رو بگیرید که انگار اونهارو اضافه کردید. با این روش میتونید درجههای بالا رو هم اضافه کنید. پس در این روش لازم نیست نگران تعداد بالای فیچر ها باشیم چون اصلا فیچری اضافه نمیکنیم. بیاید روی دیتاست Moon امتحانش کنیم:
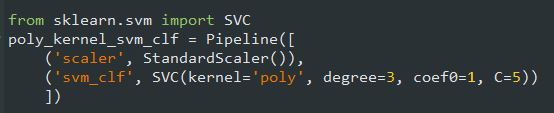
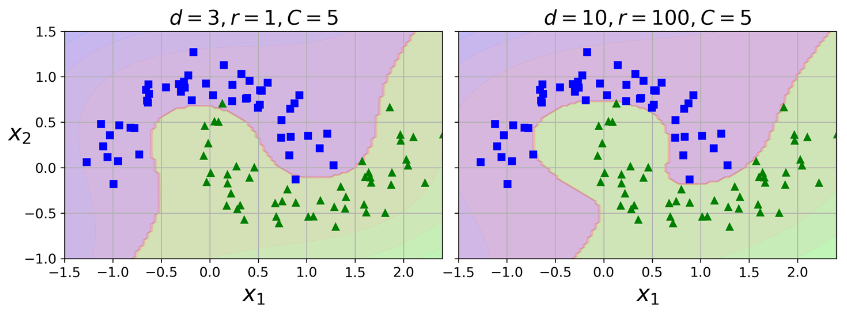
این کد با استفاده از یک کرنل درجه 3، یک SVM Classifier ترین میکنه. شکل حاصل رو میتونید در سمت چپ ببینید. در سمت راست یک مدل با کرنل درجه 10 رو میبینید. مطمئناً اگر مدل شما Overfit شده، باید درجه چندجملهای رو کم کنید. در طرف مقابل، اگر Underfit شده، باید درجه چندجملهای رو زیاد کنید. هایپرپارامتر coef0 مقدار تاثیرپذیری مدل از چندجملهای درجه بالا، در مقابل چند جملهای درجه پایین رو کنترل میکنه.
یک روش خوب برای پیدا کردن هایپرپارامتر های مناسب، استفاده از Grid Search هست. اینکه بدونید هر هایپرپارامتر دقیقا چه کاری انجام میده کمک میکنه بهتر در فضای هایپرپارامتر ها جستوجو کنید.
یک تکنیک دیگه برای حل مشکلات غیرخطی بودن، اضافه کردن فیچرهای جدید با استفاده از تابع تشابه هست. (SImilarity Function). این تابع، شبیه بودن هر نمونه به یک نقطه عطف خاص رو اندازه گیری میکنه. مثلا دیتاست یک بعدی مثال قبل رو در نظر بگیرید. دو نقطه عطف در x1 = -2 و x1 = 1 بهش اضافه میکنیم.حالا تابع تشابه رو Gaussian Radial Basis Function با مقدار گاما برابر 0.3 در نظر میگیریم.
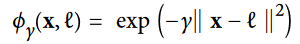
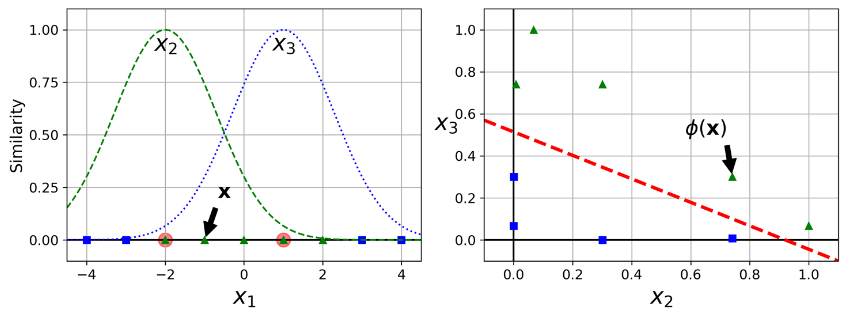
این یک تابع با شکل زنگوله هست که مقدار اون از 0 (خیلی دور از نقطه عطف) تا 1 (خود نقطه عطف) متغیر هست. حالا آماده هستیم که فیچر های جدید رو محاسبه کنیم. برای مثال نمونه واقع در x1 = -1 رو در نظر بگیرید. فاصله اون از اولین نقطه عطف برابر 1 و از دومین نقطه عطف برابر 2 هست. بههمین دلیل فیچر های جدید اون برابر x2 = exp( -0.3 * 1^2) (حدودا 0.74) و x3 = exp( -0.3 * 2^2) هست (حدودا 0.30). شکل سمت راست دیتاست ترنسفورم شده رو نشون میده(فیچر های اصلی حذف شدند) همونطور که میبینید حالا جداپذیر با خط هست.
ممکنه براتون سوال پیش اومده باشه که چطور نقاط عطف رو انتخاب کنیم. یک راه ساده اینه که در مکان هر نمونه، یک نقطه عطف درست کنیم. با این کار، بعد های زیادی تولید میکنیم و شانس جداپذیر بودن با خط دیتاست ترنسفورم شده رو افزایش میدیم. نکته منفی این روش اینه که اگر m نمونه و n فیچر داشته باشیم، ترینینگ ست تبدیل شده m نمونه و m فیچر خواهد داشت (با فرض اینکه فیچر های اصلی رو حذف کردید) اگر دیتاست شما بزرگ باشه، با همون اندازه هم فیچر های زیادی خواهید داشت.
این روش هم مثل روش Polynomial Feature با هر الگوریتم ماشین لرنینگی سازگار هست اما از لحاظ محاسباتی، محاسبه همه فیچر های اضافه مخصوصا در ترینینگ ست های بزرگ، هزینه زیادی داره. حالا بیاید این کرنل رو پیاده سازی کنیم:
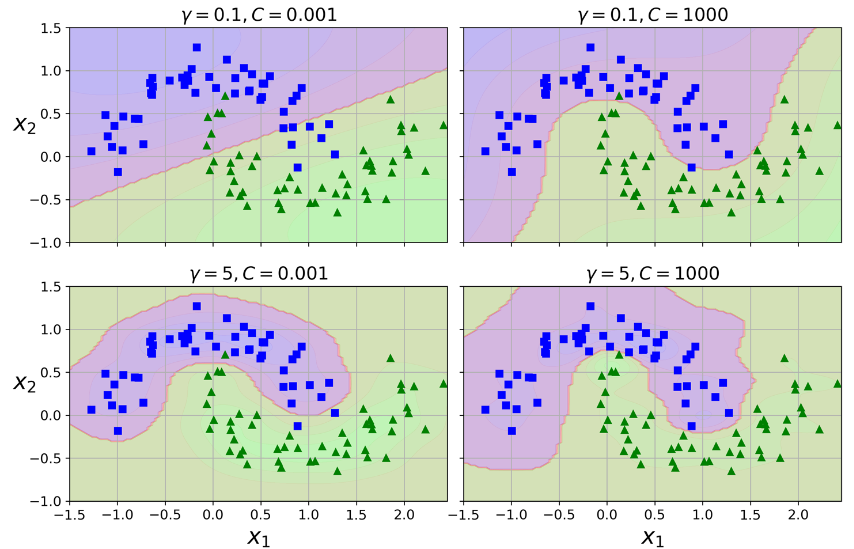
این مدل رو میتونید در پایین سمت چپ شکل زیر ببینید. شکل های دیگه نشون دهنده ای مدل هایی هستند که با هایپرپارامتر های گاما و C متفاوتی ترین شدند.با افزایش گاما، منحنی زنگولهای باریک تر و محدود تر میشه. نتیجه این کار، کوچکتر شدن رنج تاثیر هر نمونه هست: مرز تصمیمگیری نامنظمتر میشه و اطراف نمونه ها حرکت میکنه. پس در واقع گاما مثل یک هایپرپارامتر Regularization عمل میکنه: اگر مدل اورفیت شده، باید مقدارش رو کم کنید. اگر مدل آندرفیت شده، باید مقدارش رو زیاد کنید. (مثل هایپرپارامتر C)
کرنل های دیگهای هم وجود دارند اما بهندرت استفاده میشن. بعضی کرنل ها مخصوص برخی ساختمان دادهها هستند. کرنل های رشتهای (String Kernel) بعضی اوقات برای دسته بندی داده های متنی یا رشته های DNA استفاده میشن.
از بین این همه کرنل، از کدوم باید استفاده کنیم؟ طبق فانون سرانگشتی، همیشه اول از کرنل خطی استفاده کنید (یادتون باشه که LinearSVC خیلی سریعتر از SVC(kernel='linear') هست) مخصوصاً وقتی که ترینینگ ست خیلی بزرگه یا فیچر های زیادی داره. اگه دیتاست زیاد بزرگ نیست، بهتره که کرنل Gaussian RBF رو هم امتحان کنید، در بیشتر مواقع بهخوبی کار میکنه. اگر وقت و توان محاسباتی کافی دارید، میتونید کرنل های مختلف رو با استفاده از Cross-Validation و Grid Search امتحان کنید. وقتی ترینینگ ست شما ساختمان داده مخصوصی داره، پیشنهاد میشه کرنل های مختلف رو امتحان کنید.
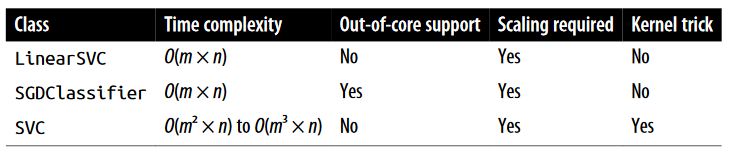
اساس کلاس LinearSVC، کتابخانه liblinear هست که برای Linear SVM یک الگوریتم بهینهشده پیادهسازی میکنه. این کلاس از کرنل پشتیبانی نمیکنه اما با توجه به تعداد نمونهها و فیچرها مقیاس خودش رو تقریباً بهصورت خطی تغییر میده. پیچیدگی زمانی ترینینگ اون O(m * n) هست.
اگر دقت بیشتری لازم دارید، این الگوریتم زمان بیشتری احتیاج داره. این مورد توسط هایپرپارامتر Tolerance کنترل میشه. (در Scikit-Learn با tol نشون داده میشه) در بیشتر طبقهبندیها، مقدار دیفالت این هایپرپارامتر کارراه انداز هست.
اساس کلاس SVC، کتابخانه libsvm هست که یک الگوریتم با پشتیبانی از کرنل پیادهسازی میکنه. پیچیدگی زمانی ترینینگ تایم معمولا بین O(m^2 * n) و O(m^3 * n) هست. متاسفانه این یعنی وقتی نمونهها زیاد هستند، به شدت آهسته میشه. این الگوریتم برای ترینینگ ست های پیچیده با اندازه کوچیک یا متوسط مناسب هست. مقیاسپذیری خوبی با تعداد فیچر ها انجام میده مخصوصا Sparse Features (یعنی وقتی که هر نمونه تعداد کمی فیچر غیرصفر داره) در این صورت، مقیاس الگوریتم با میانگین تعداد فیچر های غیرصفر هر نمونه، تقریباً تغییر میکنه.
همونطور که قبلا هم اشاره شد، الگوریتم SVM گسترده هست. نهتنها از طبقهبندی خطی و غیرخطی پشتیبانی میکنه بلکه از پس رگرسیون خطی و غیر خطی هم برمیاد. برای استفاده از SVM برای رگرسیون، کافیه هدف رو برعکس کنید: بهجای اینکه فضای میانی بین کلاس هارو تا جایی که امکان داره کوچیک کنیم تا نقض حاشیه کم بشه، رگرسیون SVM سعی میکنه تا جایی که امکان داره نمونههای زیادی رو در فضای میانی جا بده . بهطور همزمان تعداد نقض حاشیههارو پایین نگه داره. عرض این فضا توسط هایپرپارامتر اپسیلون کنترل میشه. شکلی که میبینید دو مدل رگرسیون خطی SVM رو نشون میشه با دو مقدار اپسیلون متفاوت.
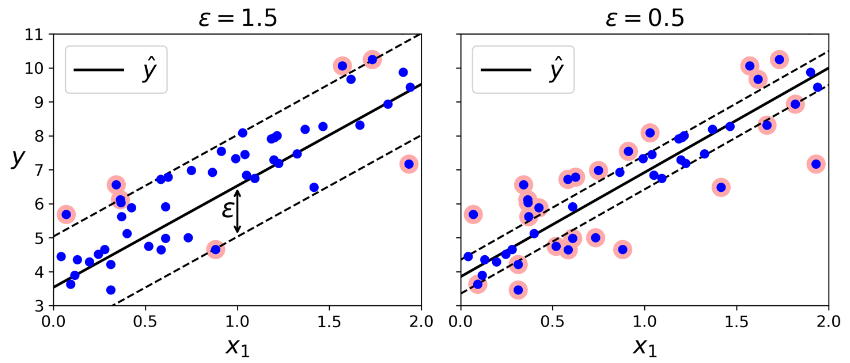
اضافه کردن نمونه های ترینینگ تاثیری در حدس های مدل ایجاد نمیکنه، در نتیجه این مدل نسبت به مقدار اپسیلون حساس نیست. (Epsilon Insensitive)
میتونید از کلاس LinearSVR برای اجرای رگرسیون خطی SVM استفاده کنید. کدی که میبینید مدل سمت چپ شکل بالا رو تولید میکنه.
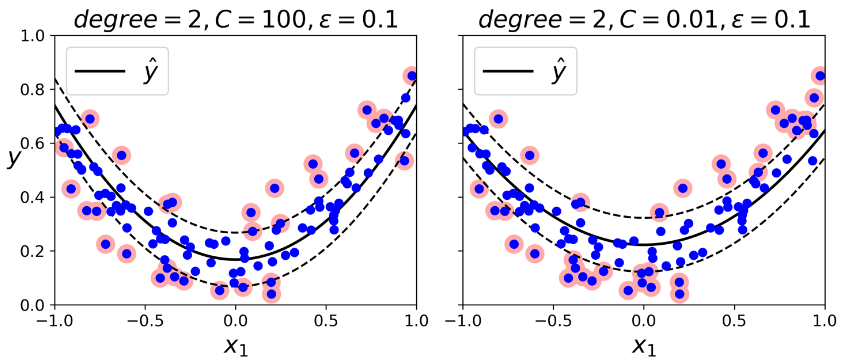
برای اجرای رگرسیون غیرخطی، میتونید از یک مدل SVM بههمراه کرنل استفاده کنید. شکلی که میبینید یک رگرسیون SVM رو روی یک ترینینگ ست درجه 2 با استفاده از کرنل درجه 2، نشون میده. مقدار Regularization شکل سمت چپ کم(مقدار C بزرگ) و شکل سمت راست زیاد هست (مقدار C کوچیک)
کدی که میبینید از کلاس SVR استفاده میکنه تا مدل سمت چپ شکل رو ایجاد کنه. این کلاس از کرنل پشتیبانی میکنه.

در واقع کلاس SVR معادل رگرسیون کلاس SVC و کلاس LinearSVR معادل رگرسیون کلاس LinearSVC هست. کلاس LinearSVR متناسب با اندازه ترینینگ ست، بهصورت خطی تغییر میکنه(درست مثل LinearSVC) در حالیکه کلاس SVR وقتی ترینینگ ست بزرگ میشه، خیلی آروم عمل میکنه (مثل SVC)
الگوریتم های SVM برای تشخیص دادههای پرت هم کاربرد دارن. برای اطلاعات بیشتر به داکیومنت Scikit-Learn مراجعه کنید
خب این هم از بررسی الگوریتم SVM. امیدوارم مفید واقع شده باشه.