بررسی الگوریتم های رگرسیون در ماشین لرنینگ

توی مطالب قبلی ما با مدل های ماشین لرنینگ کار کردیم. تا به اینجای کار الگوریتم ها برای ما مثل جعبه سیاه بودن. دونستن طرز کار هر الگوریتم به ما کمک میکنه که که الگوریتم مناسب رو به همراه هایپرپارامتر های ایده‌آل انتخاب کنیم. همچنین باعث میشه که مشکلات پیش اومده رو به راحتی حل کنیم و از بروز مشکلات بعدی جلوگیری کنیم. توی این مطلب میخوایم مدل رگرسیون خطی رو بررسی کنیم.

رگرسیون خطی

یک مدل Linear Regression با محاسبه یک حاصل جمع وزن دار از فیچر ها و یک ثابت به نام Bias Term یا Intercept Term ، یک حدس میزنه. معادله رگرسیون خطی رو میتونید مشاهده کنید:

این معادله رو میتونیم با استفاده از بردار، خلاصه تر هم بنویسیم:

در ماشین لرنینگ بردار ها معمولا بصورت بردار های ستونی، که آرایه های دو بعدی با یک ستون هستند، نشون داده میشن. اگه θ و x بردار های ستونی باشن، مقدار حدس زده شده برابر هست با ضرب x در ماتریس ترانهاده θ یا Transpose θ.

خب این از رگرسیون خطی. ولی چطور ترین کنیم ؟ یادتون باشه توی مطلب قبلی گفتیم ترین یک مدل یعنی تنظیم پارامتر های این مدل بطوری که بهترین عملکرد رو روی ترینینگ ست نشون بده. برای این کار، اول به یک معیار احتیاج داریم که بدونیم مدل چجوری عمل میکنه. همچنین گفتیم که یکی از رایج ترین راه ها استفاده از RMSE هست. پس برای یک مدل رگرسیون خطی، باید مقدار θ رو جوری پیدا کنیم که RMSE رو به کمترین حد برسونه. در عمل، ساده تر هست که مقدار MSE رو کم کنیم چون این کار مقدار RMSE رو هم کم میکنه. (وقتی یک عدد کوچیک بشه ، جذرش هم کوچیک میشه)

فرمول MSE رو میتونید ببینید:

معادله نرمال

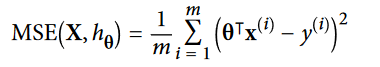
برای پیدا کردن مقدار θ ای که مقدار تابع هزینه (Cost Function) رو به حداقل میرسونه، از یک معادله به نام معادله نرمال یا Normal Equation استفاده میکنیم.

حالا بیاید چند تا داده خطی درست کنیم تا این معادله رو امتحان کنیم. معادله ای که ازش استفاده میکنیم y= 4 + 3x + noise هست.دقت کنید که بخاطر رندوم بودن داده ها، شکل و اعدادی که بدست میارید متفاوت خواهند بود:

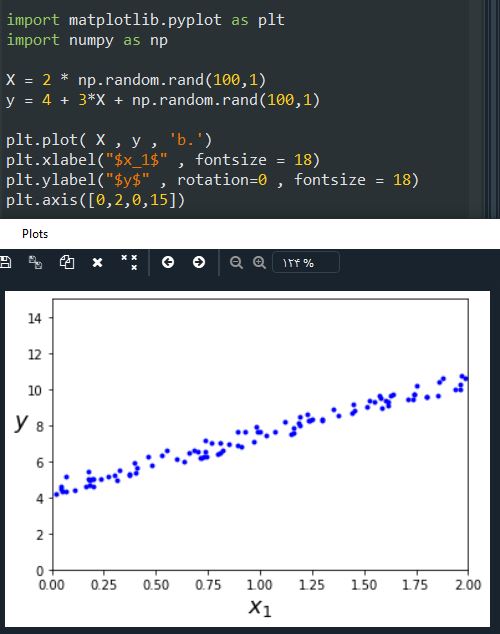
حالا بیاید تتا هت رو با استفاده از معادله نرمال محاسبه کنیم. برای این کار اول از تابع inv ، واقع در ماژول np.linalg ، استفاده میکنیم تا معکوس ماتریس رو محاسبه کنیم و از تابع dot استفاده میکنیم تا ضرب ماتریس ها رو انجام بدیم:

چیزی که در بهترین حالت رخ میده و ما امیدوار بودیم که رخ بده، این بود که مقدار تتا صفر برابر 4 و تتا 1 برابر 3 بشه ولی خب 4.33 و 3.11 شده. به اندازه کافی نزدیک هست. علت اینکه نتونسته مقدار دقیق رو به دست بیاره این هست که ما به داده ها نویز اضافه کردیم. (چیزی که در واقعیت هم در داده ها رخ میده)

حالا با استفاده از تتا هت بدست اومده میخوایم یک حدس بزنیم:

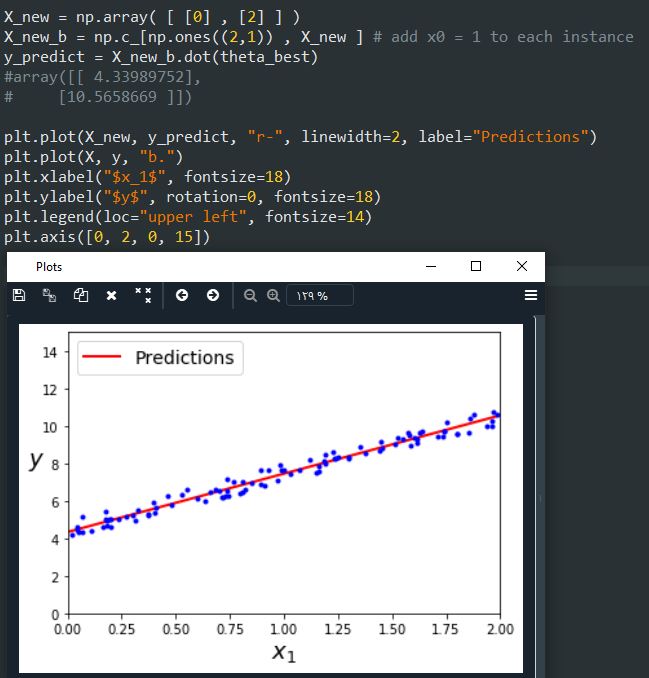
پیاده سازی رگرسیون خطی با استفاده از Scikit-Learn ساده است. برای دسترسی به وزن فیچر ها از coef و میزان خطا از intercept استفاده میکنیم:

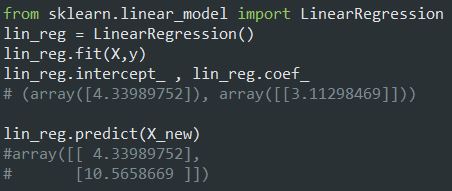
کلاس LinearRegression بر پایه تابع scipy.linalg.lstsq هست (تابع برای محاسبه Least Square) که میتونیم به طور مستقیم فراخوانی کنیم:

این تابع ، این مقدار رو محاسبه میکنه. توی این فرمول، ایکس مثبت مقدار ماتریس شبه-وارون هست ( به طور دقیق تر ، Moore-Penrose Inverse ) میتونیم از تابع np.linalg.pinv برای محاسبه استفاده کنیم:

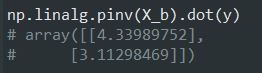
ماتریس شبه-وارون توسط یک تکنیک به نام Singular Value Decomposition محاسبه میشه. برای درک بهتر این فرمول میتونید این لینک رو بخونید. این راه کارآمد تر از محاسبه معادله نرمال هست و حتی اگه ماتریس مورد نظر وارون پذیر نباشه، همچنان میتونه ماتریس وارون رو محاسبه کنه.

پیچیدگی محاسباتی

معادله نرمال، حاصل ضرب ماتریس X در ترانهاده X رو معکوس میکنه. این ماتریس یک ماتریس n+1 در n+1 هست که n تعداد فیچر هاست. پیچیدگی محاسباتی محاسبه همچین ماتریسی بین O(n^2.4) تا O(n^3) هست.

هر دوی معادله نرمال و SVD، با افزایش تعداد فیچر ها، به شدت کند میشن. البته نکته مثبت این دو، خطی بودن اون هاست که باعث میشه در صورت وجود حافظه به اندازه کافی، ترینیگ ست های بزرگ رو مدیریت کنن

همچنین، وقتی مدل رگرسیون خطی رو ترین کردیم ( حالا یا با روش معادله نرمال یا هر روش دیگه ای ) حدس ها سریع تر انجام میشن چون پیچیدگی محاسباتی خطی هست. به عبارت دیگه، با دو برابر شدن داده ها یا فیچر ها، زمان هم دو برابر میشه.

حالا یک روش دیگه برای ترین یک مدل رگرسیون خطی معرفی میکنیم که مناسب وقت هایی هست که تعداد فیچر ها یا نمونه ها خیلی زیاد هست و توی حافظه جا نمیشن.

گرادیان کاهشی

گرادیان کاهشی (Gradient Descent) یک الگوریتم بهینه سازی هست که میتونه راه حل بهینه رو برای مسائل گوناگونی پیدا کنه. ایده GD این هست که پارامتر ها رو برای کم شدن تابع هزینه، بصورت تکرار شونده (iteratively) بهینه سازی کنیم.

فرض کنید توی مه در یک کوهستان گم شدید و فقط میتونید شیب زمین زیر پاتون رو حس کنید. یک استراتژی خوب برای رسیدن به پایین دره این هست که به جهت تند ترین شیب به پایین دره حرکت کنیم. این کاری هست که GD انجام میده: گرادیان محلی تابع خطا رو با توجه به تتا محاسبه میکنه و در جهتی حرکت میکنه که گرادیان کاهش پیدا میکنه. وقتی گرادیان صفر بشه ، به مینیمم رسیدیم!

در آغاز، یک مقدار رندوم به تتا میدیم (به این کار میگن Random Initialization). بعد با برداشتن قدم های کوچیک، سعی میکنیم که گرادیان رو بهتر کنیم و مقدار تابع هزینه (MSE) رو کم کنیم تا جایی که الگوریتم همگرا به مینیمم بشه.

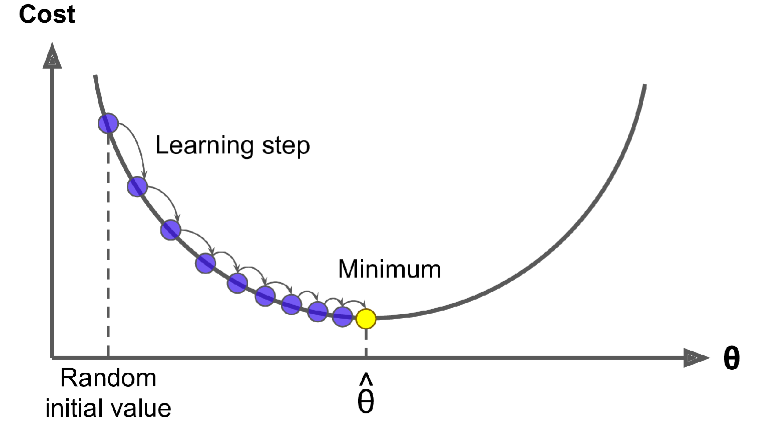
یک پارامتر مهم در گرادیان کاهشی، اندازه قدم ها هست که توسط هایپرپارامتر Learning Rate مشخص میشه. اگه LR خیلی کوچیک باشه، الگوریتم تکرار های زیادی رو برای همگرایی انجام میده و زمان زیادی طول میکشه.

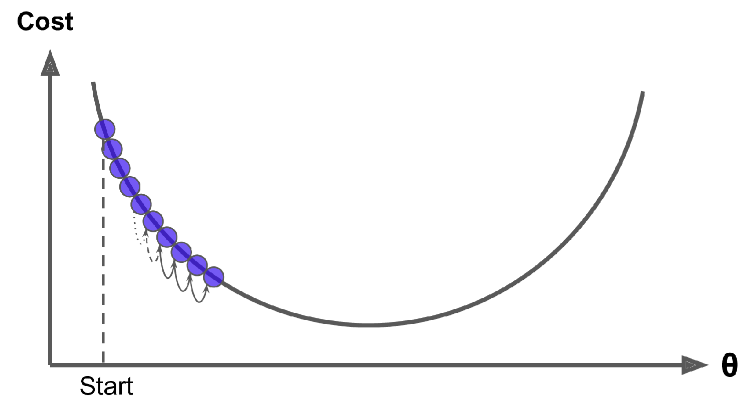
اگر LR خیلی زیاد باشه، ممکنه به جهات مختلف پرش کنیم و الگوریتم نتونه مقدار مناسب رو پیدا کنه و واگرایی رخ میده.

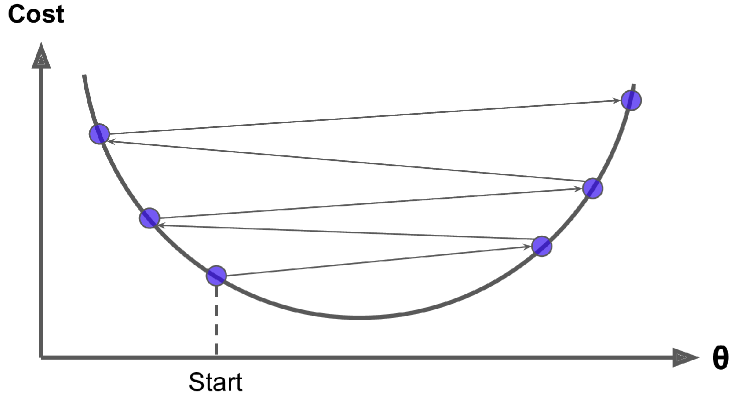
و در آخر، این نکته رو در نظر داشته باشید که همه تابع های هزینه، ظاهر خوبی ندارن و لزوما به شکل کاسه نیستند. ممکنه سوراخ، چاله ،پشته و یا هر جور بالا پایینی وجود داشته باشه که باعث بشه پیدا کردن مینیمم کار سختی بشه. شکل زیر دو تا از چالش های GD رو نشون میده. اگر Random Initialization در طرف چپ باشه، اونوقت به یک مینیمم محلی همگرا میشه که به خوبی مینیمم سراسری نیست. اگر در طرف راست باشه، زمان خیلی زیادی طول میکشه تا قسمت مسطح رو رد کنه. اگر هم خیلی زود بایسیتیم، هیچوقت نمیتونیم به مینیمم سراسری برسیم.

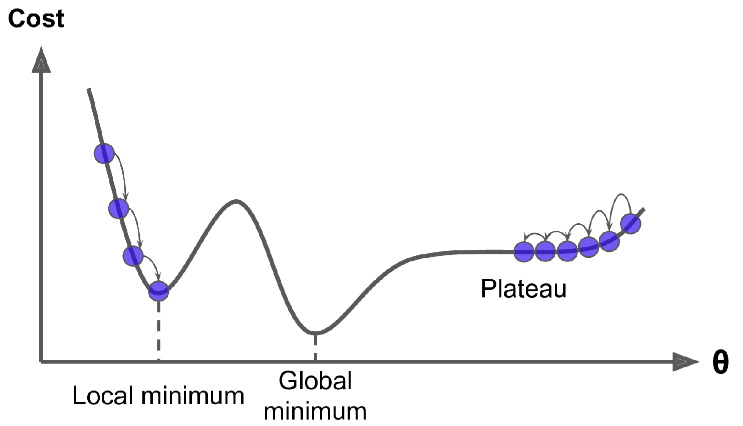
خوشبختانه MSE برای یک مدل رگرسیون خطی یک تابع محدب (Convex Function) هست. به این معنی که اگر هر دو نقطه دلخواه روی این محدب رو انتخاب کنید، خط بین این دو نقطه هیچگاه از محدب رد نمیشه؛ یعنی هیچ مینیمم محلی ای وجود نداره و فقط یک مینیمم سراسری وجود داره. همچنین یک تابع پیوسته هست که شیب اون هیچوقت ناگهانی تغییر نمیکنه. این دو فاکتور باعث میشن که گرادیان کاهشی به اندازه کافی به مینیمم سراسری نزدیک بشه (البته اگر به اندازه کافی صبر کنیم و LR هم زیاد نباشه)

در واقع تابع هزینه شکل کاسه مانندی داره اما اگر فیچر ها در مقیاس های متفاوت باشن، میتونه دراز بشه. شکل زیر گرادیان کاهشی رو روی یک ترینینگ ست نشون میده که سمت چپ فیچر 1 و 2 مقیاس های برابر دارن و سمت راست مقادیر فیچر 1 کوچک تر از فیچر 2 هست.

(چرا شکل در طول فیچر 1 کشیده شده ؟ چون این فیچر کوچک تر هست و برای تاثیرگذاری روی تابع هزینه، این فیچر باید تغییر بیشتری بکنه. بخاطر همین شکل در طول این فیچر کشیده شده)

همونطور که میبینید در شکل چپ، الگوریتم مستقیم میره به سمت مینیمم و به سرعت اون رو پیدا میکنه. در حالیکه در سمت راست اول در جهتی که تقریبا با مینیمم زاویه 90 درجه داره حرکت میکنه و بعدش آروم آروم به سمت مینیمم نزدیک میشه. در نهایت هم به مینیمم میرسه ولی خب زمان بیشتری طول میکشه.

وقتی از گرادیان کاهشی استفاده میکنیم، حتما باید مطمئن باشیم که همه فیچر ها در مقیاس برابر هستند وگرنه برای همگرایی زمان زیادی لازم میشه. برای تغییر مقیاس هم از کلاس StandardScaler واقع در کتابخانه Scikit-Learn استفاده میکنیم.

شکل بالا همچنین نشون میده که ترین یک مدل یعنی جستجو برای پیدا کردن ترکیبی از پارامتر ها که تابع هزینه رو به حدقل میرسونه. در واقع یک جستجو در فضای پارامتر های مدل هست: هر چقدر که مدل پارامتر های بیشتری داشته باشه، فضای مدل ابعاد بیشتری داره و جستجو هم سخت تر میشه. پیدا کردن سوزن تو انبار کاه 300 بعدی سخت تر از 3 بعدی هست. خوشبختانه، چون تابع هزینه برای رگرسیون خطی به شکل کاسه هست، سوزن در پایین کاسه قرار داره.

گرادیان کاهشی دسته‌ای

برای استفاده از گرادیان کاهشی، باید گرادیان تابع هزینه رو با توجه به هر پارامتر مدل محاسبه کنیم. به عبارت دیگه، باید مقدار تغییر تابع هزینه با تغییر تتا رو محاسبه کنیم. به این کار میگن مشتق جزئی. مثل این میمونه که سوال بپرسید "اگر به سمت شرق برم، شیب زمین کوهستان زیر پام چقدر تغییر میکنه ؟ " و همین سوال رو درباره شمال و تمام ابعاد موجود بپرسید. معادله ای که در زیر میبینید مشتق جزئی تابع هزینه رو محاسبه میکنه:

به جای محاسبه تک تک مشتق های جزئی، میتونیم از معادله پایین استفاده کنیم تا یک دفعه تمام محاسبات رو انجام بده. بردار گرادیان که در زیر میبینید، شامل همه مشتق های جزئی تابع هزینه هست (برای هر پارامتر مدل):

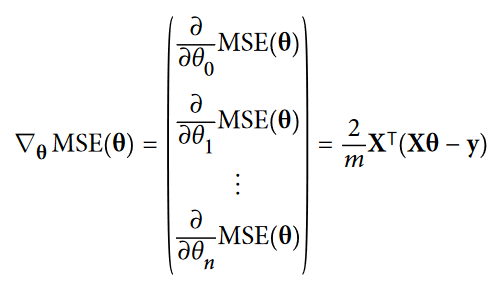
توجه کنید که این فرمول در هر قدم گرادیان کاهشی، محاسبات رو برای همه ترینینگ ست انجام میده! بخاطر همین بهش میگن گرادیان کاهشی دسته‌ای (Batch Gradient Descent) چون در هر قدم از کل ترینینگ ست استفاده میکنه. بخاطر همین روی ترینینگ ست های بزرگ به شدت کند هست (در ادامه الگوریتم های گرادیان کاهشی با سرعت بیشتر رو هم خواهیم دید). گرچه، گرادیان کاهشی با افزایش تعداد فیچر ها، به خوبی میتونه خودش رو تطبیق بده؛ بطوریکه ترین یک مدل رگرسیون خطی با هزاران فیچر با استفاده از گرادیان کاهشی، سریع تر از استفاده از معادله نرمال یا SVD هست

بردار گرادیان به سمت بالا هست. بعد از محاسبه این بردار، کافیه که در جهت مخالف و به سمت پایین حرکت کنیم. معادله ای که پایین می‌بینید بیان کننده همین موضوع هست. توی این فرمول Eta نشون دهنده اندازه قدم های رو به پایین ما هست:

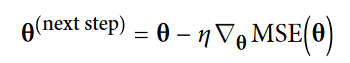
حالا میخوایم این الگوریتم رو پیاده سازی کنیم:

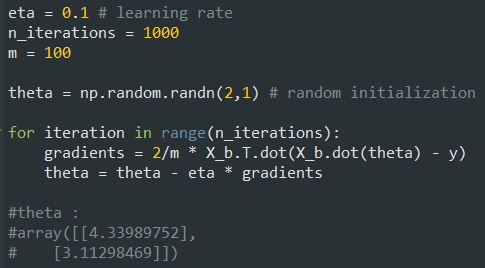
خب این مقداری هست که معادله نرمال هم پیدا کرده بود. این یعنی گرادیان کاهشی ما به خوبی کار میکنه. توی تصاویر زیر میتونید حالاتی رو ببینید که مقادیر eta یا Learning Rate متفاوت هست:

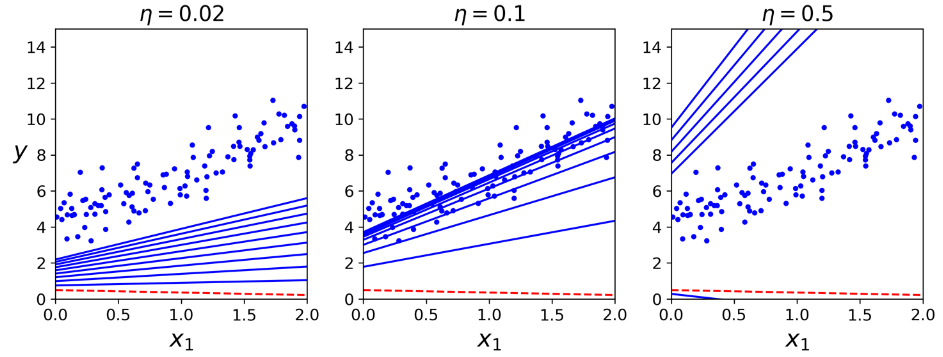
در سمت چپ LR کم هست. الگوریتم در نهایت به راه حل میرسه اما خب زمان زیادی طول میکشه. عکس وسط خوب به نظر میاد. فقط با چند تکرار تونسته به راه حل نزدیک بشه. عکس سمت راست LR زیاد هست. الگوریتم از راه حل دور تر میشه و فقط از جایی به جای دیگه میپره.

برای پیدا کردن یک LR خوب، میتونیم از Grid Search استفاده کنیم. بهتر هست که تعداد تکرار ها رو کم کنید تا GS مدل هایی رو که خیلی طول میکشن به راه حل نزدیک بشن، حذف کنه.

ممکنه براتون سوال پیش بیاد که چطور باید تعداد تکرار ها رو مشخص کرد. اگر خیلی کم باشه، ممکنه الگوریتم موقعی که هنوز فاصله زیادی با راه حل داریم، بایسته. اگر خیلی زیاد باشه، زمان زیادی رو، در حالی که پارامتر ها هم تغییری نمیکنن، تلف کردیم. یک راه حل ساده اینه که تعداد تکرار ها رو زیاد بذاریم اما هر وقت بردار گرادیان خیلی کوچیک شد، الگوریتم رو متوقف کنیم. یعنی وقتی که نرم بردار از یک مقدار کوچیکی به نام tolerance کمتر شد چون این اتفاق موقعی میفته که گرادیان کاهشی تقریبا به مینیمم رسیده. (tolerance رو با این نماد نشون میدن)

نرخ همگرایی
وقتی تابع هزینه به شکل محدب هست و شیب‌ش ناگهانی تغییر نمیکنه، استفاده از Batch Gradient Descent به‌همراه یک LR ثابت ما رو به راه حل میرسونه اما باید کمی صبر کنیم. بسته به شکل تابع هزینه، میتونه به این تعداد تکرار طول بکشه تا به راه حل برسیم. اگر Tolerance رو تقسیم بر 10 کنیم تا به دقت بیشتری برسیم، اونوقت زمان اجرای الگوریتم 10 برابر بیشتر میشه.

گرادیان کاهشی نامنظم

مشکل اصلی Batch Gradient Descent این هست که برای محاسبه گرادیان از کل ترینینگ ست استفاده میکنه که باعث میشه زمان زیادی طول بکشه. در حالیکه Stochastic Gradient Descent در هر قدم بصورت رندوم یک نمونه از ترینینگ ست رو انتخاب میکنه و گرادیان رو بر اساس اون نمونه محاسبه میکنه. مطمئناً استفاده از یک نمونه به‌جای کل نمونه ها، زمان محاسبه رو کم میکنه. همچنین با استفاده از این روش، کار با دیتاست های بزرگ هم امکان پذیر میشه چون در هر تکرار فقط یک نمونه در حافظه قرار میگیره.

از طرف دیگه، بخاطر Stochastic یا همون رندوم بودن این الگوریتم، در مقایسه با Batch Gradient Descent کمتر منظم هست چون به جای آروم آروم کم کردن مقدار برای رسیدن به مینیمم، تابع هزینه مکرر بالا پایین میشه. با گذشت زمان به مینیمم میرسه اما وقتی به اونجا برسه آروم نمیشه بلکه به اطراف حرکت میکنه. پس وقتی الگوریتم می‌ایسته، مقدار پارامتر های نهایی خوب هستن ولی ایده‌آل نیستند.

وقتی تابع هزینه شکل نامنظم داشته باشه، این الگوریتم میتونه از مینیمم محلی بپره. پس SGD در مقابل BGD، شانس بهتری برای پیدا کردن مینمم سراسری داره.

به‌خاطر همین، رندوم بودن برای فرار از مینیمم محلی خوبه اما چون باعث میشه الگوریتم هیچوقت توی مینیمم متوقف نشه، بده. یک راه حل برای این دو راهی اینه که رفته رفته LR رو کم کنیم. قدم ها بزرگ آغاز میشن (که باعث میشه سریع پیشرفت کنیم و از مینیمم محلی عبور کنیم) بعد کوچکتر و کوچکتر میشن. این به الگوریتم اجازه میده که توی مینیمم سراسری بایسته. تابعی که در هر تکرار مقدار LR رو مشخص میکنه Learning Schedule نام داره. اگر LR خیلی سریع کم بشه، ممکنه تو مینیمم محلی گیر کنیم. اگر LR خیلی آروم کم بشه، ممکنه برای مدت طولانی دور مینیمم بچرخیم و آخر هم توی یک راه حل نیمه بهینه بایسیتم.

این کد با استفاده از یک LS ساده الگوریتم SGD رو پیاده سازی میکنه:

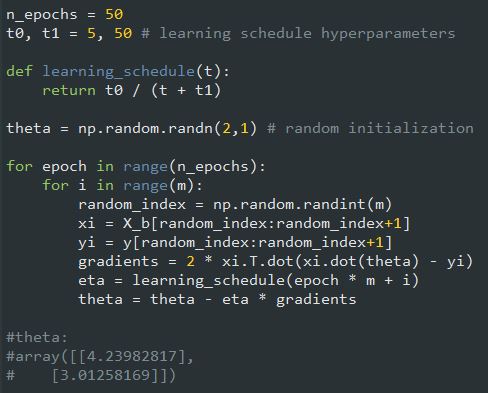
به طور قراردادی تعداد تکرار ها رو برابر m گذاشتیم ( m در تصاویر بالاتر مقدار دهی شده) هر دور رو میگن epoch. در حالیکه BGD هزار بار کل ترینینگ ست رو تکرار کرد، این کد فقط 50 بار تکرار میکنه و به راه حل خوبی هم میرسه.

دقت کنید چون نمونه ها رو رندوم انتخاب میکنیم، بعضی نمونه ها ممکنه چند بار انتخاب و بعضی هم اصلا انتخاب نشن. اگر میخواید مطمئن باشید که این اتفاق نمیفته، میتونید ترینینگ ست رو Shuffle کنید. بعد دونه دونه هر نمونه رو انتخاب کنید و بعد دوباره Shuffle کنید. اگرچه که، این راه حل آروم به نتیجه میرسه.

وقتی از SGD استفاده میکنیم، نمونه ها باید مستقل و به طور یکسان توزیع شده باشند (IID) تا مطمئن بشیم پارامتر ها به سمت مینیمم سراسری کشیده میشن. یک راه ساده برای این کار، شافل کردن نمونه ها هنگام ترینینگ هست (انتخاب هر نمونه بصورت رندوم یا شافل کردن ترینینگ ست در آغاز هر تکرار) برای مثال اگر نمونه ها بر اساس لیبل مرتب شده باشند و ما اونهارو شافل نکنیم، SGD شروع به بهینه شدن برای یک لیبل میکنه و همینطور ادامه میده و در نهایت هم به مینیمم سراسری نمیرسه

اگر بخوایم رگرسیون خطی رو با استفاده از SGD اعمال کنیم، میتونیم از کلاس SGDRegressor استفاده کنیم. دیفالت این کلاس بهینه سازی MSE هست. کدی که پایین میبینید برای 1000 بار تکرار میشه تا موقعی که هزینه در هر تکرار به زیر 0.0001 برسه (max_iter=1000, tol=1e-3) مقدار LR اولیه برابر با 0.1(eta0=0.1) و از Regularization هم استفاده نمیکنه (penalty=None ، بعدا درباره این پارامتر صحبت میکنیم). در آخر هم به راه حلی میرسیم که نزدیک به جواب معادله نرمال هست:

گرادیان کاهشی با دسته کوچک

آخرین الگوریتم گرادیان کاهشی، Mini-batch Gradient Descent نام داره. اگه دو تا الگوریتم قبلی رو فهمیده باشید، این کاری نداره. این الگوریتم، در هر قدم به جای اینکه گرادیان رو بر اساس همه ترینینگ ست محاسبه کنه (BGD) یا بر اساس یک نمونه محاسبه کنه (SGD)، از یک دسته رندوم و کوچیک ترینینگ ست استفاده میکنه که بهش میگن Mini-batch. نکته مثبت Mini-batch GD نسبت به Stochastic GD این هست که میتونیم با بهینه سازی سخت افزار برای عملیات ماتریسی، به عملکرد بهتری برسیم، مخصوصاً وقتی که از GPU استفاده میکنیم. ( آیا دیپ لرنینگ به کارت گرافیک احتیاج دارد؟ )

روند پیشرفت این الگوریتم در فضای پارامتر ها به نسبت باقی الگوریتم ها، کمتر پراکنده هست. همونطور که میبینید، MbGD به نسبت SGD یه کمی بیشتر نزدیک مینیمم میشه ولی فرار از مینیمم های محلی براش سخت هست (این برای مسائلی که توشون مینیمم محلی وجود داره صادق هست نه رگرسیون خطی) در شکل زیر میتونید مسیر هایی رو که این سه الگوریتم گرادیان در فضای پارامتر ها طی میکنن، ببینید. هر سه در نهایت به مینیمم سراسری رسیدن اما BGD در مینیمم می‌ایسته، در حالیکه دو الگوریتم دیگه به حرکت دور مینیمم ادامه میدن. البته فراموش نکنید که BGD زمان زیادی رو در هر قدم سپری میکنه؛ و اگر از یک Learning Schedule خوب استفاده کرده باشید، میتونید با این دو الگوریتم هم به مینیمم برسید.

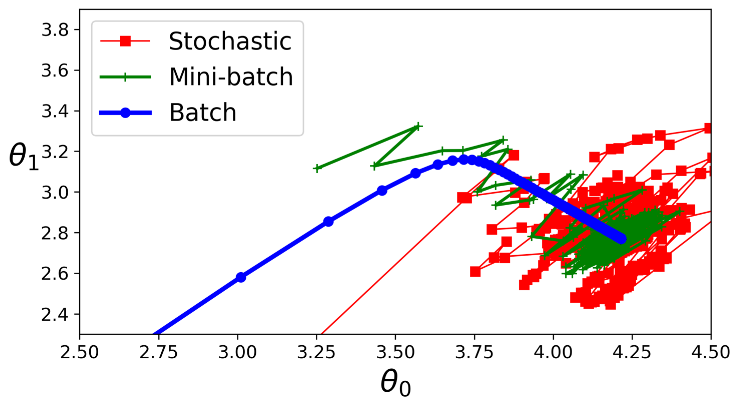
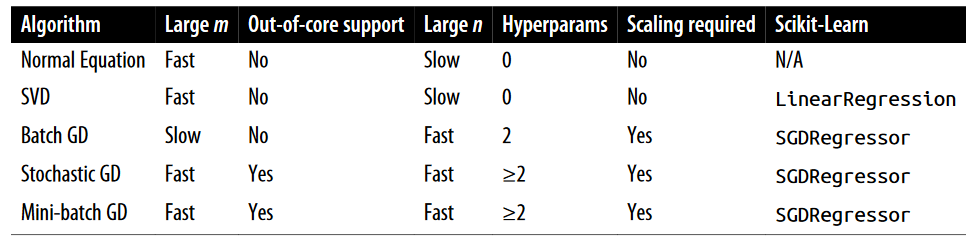
حالا بیاید این الگوریتم ها رو برای رگرسیون خطی مقایسه کنیم.

نکته اول : معادله نرمال فقط در رگرسیون خطی کاربرد داره. اما از گرادیان کاهشی میشه برای مدل های دیگه هم استفاده کرد
نکته دوم : m تعداد نمونه های ترینینگ هست و n تعداد فیچر هاست
نکته سوم : بعد از اتمام ترینینگ، هیچ فرقی بین مدل هایی که از طریق این الگوریتم ها به دست میاریم، وجود نداره و در نهایت به یک روش روند حدس انجام میشه

رگرسیون چند جمله ای

اگه داده هامون پیچیده تر از یک خط مستقیم باشن چی؟ خوشبختانه میتونیم از یک مدل خطی برای داده های غیرخطی استفاده کنیم. یک راه ساده برای انجام این کار، اضافه کردن توان های هر فیچر به عنوان یک فیچر جدید هست. بعد با استفاده از این فیچر های جدید، یک مدل خطی رو ترین میکنیم. این تکنیک Polynomial Regression نام داره.

بیاید یک مثال ببینیم. اول با استفاده از یک معادله درجه دو یک سری داده غیر خطی درست میکنیم:

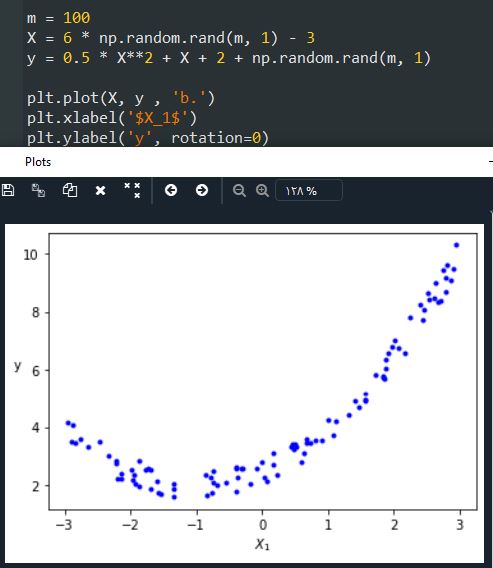
خب همونطور که مشخصه یک خط صاف هیچوقت با این داده ها تطابق پیدا نمیکنه. بخاطر همین از کلاس PolynomialFeatures برای ترنسفورم ترینینگ دیتا استفاده میکنیم و بعد مربع هر فیچر رو محاسبه میکنیم و بعنوان فیچر جدید اضافه میکنیم:

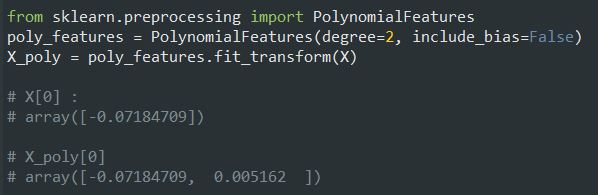
حالا X_poly شامل فیچر های اصلی به اضافه مربع اون فیچر هاست. میتونیم این داده ها رو به یک مدل رگرسیون خطی بدیم:

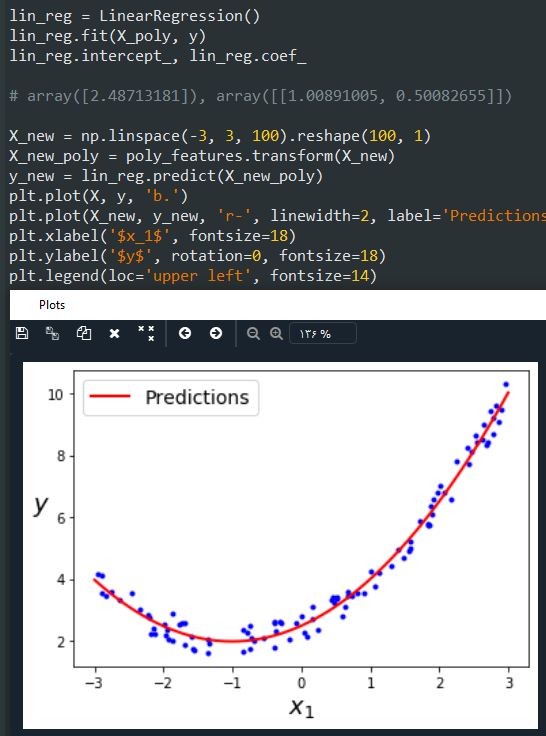
عملکرد مدل خوبه. تابع اصلی ما y = 0.5x^2 + 1.0x + 2.0 بود، چیزی که مدل به دست آورده حدودا برابر y = 0.5x^2 + 1.0x + 2.48 هست.

توجه کنید که موقعی که چند تا فیچر هست، Polynomial Regression میتونه رابطه بین فیچر ها رو بدست بیاره (Linear Regression نمیتونه). علت این توانایی این هست که PolynomiaFeatures تمام حالات فیچر ها رو تا اون درجه ای که ما مشخص کردیم اضافه میکنه. برای مثال، اگه دو فیچر a و b داشتیم و درجه رو 3 مشخص کرده بودیم، نه تنها فیچر های a^3 , a^2 , b^3 , b^2 اضافه میشد، بلکه ab , a^2b و ab^2 هم اضافه میشدن.

کلاس PolynomialFeatures با درجه d، یک آرایه شامل n فیچر رو به یک آرایه شامل (d!n!)/!(n+d) فیچر تبدیل میکنه. دقت کنید که عدد حاصل ممکنه خیلی بزرگ باشه!

منحنی های یادگیری

اگر از یک Polynomial Regression با درجه بزرگ استفاده کنید، احتمالا مدل به نسبت Linear Regression تطابق بهتری با داده ها پیدا کنه. برای مثال عکس زیر یک مدل با درجه 300 رو نشون میده و اون رو با درجه 1 و 2 مقایسه میکنه. توجه کنید که مدل با درجه 300 چقدر سعی میکنه خودش رو به نمونه ها نزدیک کنه:

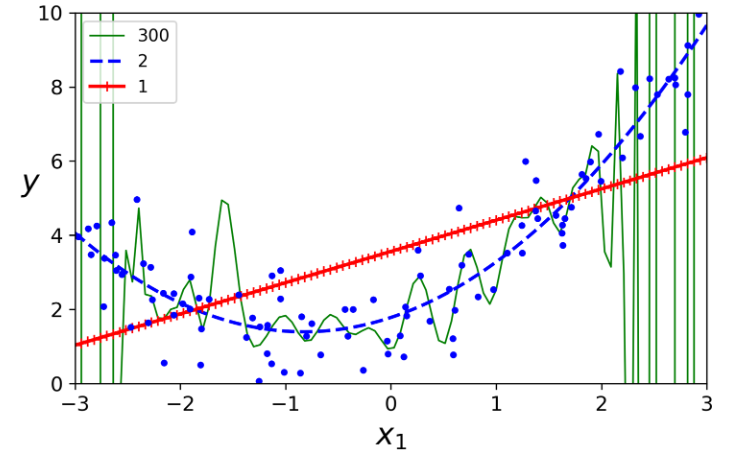
مدل با درجه 300 اورفیت و مدل با درجه 1 آندرفیت شده. بهترین حالت برای این مدل استفاده از درجه 2 هست و این حالت منطقی هم هست؛ چون داده ها با استفاده از یک معادله درجه 2 ساخته شدند. اما در حالت کلی ما اطلاعی از تابعی که داده ها رو تولید کرده نداریم. پس چطور میتونیم درمورد پیچیدگی مدل تصمیم بگیریم؟ چطور میتونیم بگیم که مدل اورفیت یا آندرفیت شده؟

توی مطالب قبل، از Cross-Validation استفاده کردیم تا عملکرد مدل رو تخمین بزنیم. اگر یک مدل روی ترنینگ دیتا عالی عمل کنه اما توی CV عملکرد بدی داشته باشه، مدل اورفیت شده و اگر در هر دو عملکرد بدی داشته باشه، آندرفیت شده. این یک راه برای فهمیدن سادگی یا پیچیدگی مدل هست.

یک راه دیگه استفاده از منحنی های یادگیری (Learning Curves) هست. این نمودار ها نشون دهنده عملکرد مدل روی ترینینگ ست و ولیدیشن ست هست. برای تولید این نمودار ها، چندین بار مدل رو با زیر مجموعه هایی با اندازه مختلف ترین میکنیم. تابعی که پایین می‌بینید، با دریافت چند داده ترینینگ، منحنی یادگیری مدل رو رسم میکنه:

from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
def plot_learning_curves(model, X, y):
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=10)
train_errors, val_errors = [], []
for m in range(1, len(X_train)):
model.fit(X_train[:m], y_train[:m])
y_train_predict = model.predict(X_train[:m])
y_val_predict = model.predict(X_val)
train_errors.append(mean_squared_error(y_train[:m], y_train_predict))
val_errors.append(mean_squared_error(y_val, y_val_predict))
plt.plot(np.sqrt(train_errors), "r-+", linewidth=2, label="train")
plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="val")
plt.legend(loc="upper right", fontsize=14)
plt.xlabel("Training set size", fontsize=14)
plt.ylabel("RMSE", fontsize=14)
lin_reg = LinearRegression()
plot_learning_curves(lin_reg, X, y)

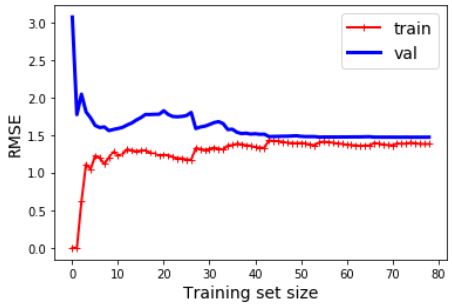
این مدل آندرفیت شده و احتیاج به کمی توضیح داره. اول به عملکرد روی ترینینگ دیتا توجه کنید. وقتی یک یا دو تا نمونه توی ترینینگ دیتا وجود داره، مدل به راحتی میتونه با اونها تطابق پیدا کنه. بخاطر همین هست که منحنی از صفر شروع میشه. اما همینطور که نمونه های تازه اضافه میشن، مدل نمیتونه با همه اونها تطابق پیدا کنه چون هم داده ها نویز زیادی دارن و اینکه داده ها اصلا خطی نیستند. این روند افزایش خطا تا جایی پیش میره که به یک سطح مسطح میرسه و دیگه با افزایش نمونه مقدار خطا تغییری نمیکنه. حالا بیاید به عملکرد مدل روی ولیدیشن ست نگاه کنیم. وقتی مدل با نمونه های کمی ترین میشه، نمیتونه به خوبی تطابق پیدا کنه. بخاطر همین در ابتدا مقدار خطا زیاد هست. بعد با افزایش تعداد نمونه ها، مدل یاد میگیره و خطا هم کاهش پیدا میکنه. این منحنی ها برای یک مدل که آندرفیت شده عادیه. هر دوی منحنی ها به یک سطح مسطح میرسن که نزدیک هم هستند و مقدار زیادی هم دارن.

اگر مدل آندرفیت شده، زیاد کردن نمونه های ترینینگ تاثیری ایجاد نمیکنه. به جای این کار، باید از مدل پیچیده تر یا فیچر های بهتر استفاده کرد

حالا بیاید به منحنی یادگیری یک مدل با درجه 10 نگاه کنیم:

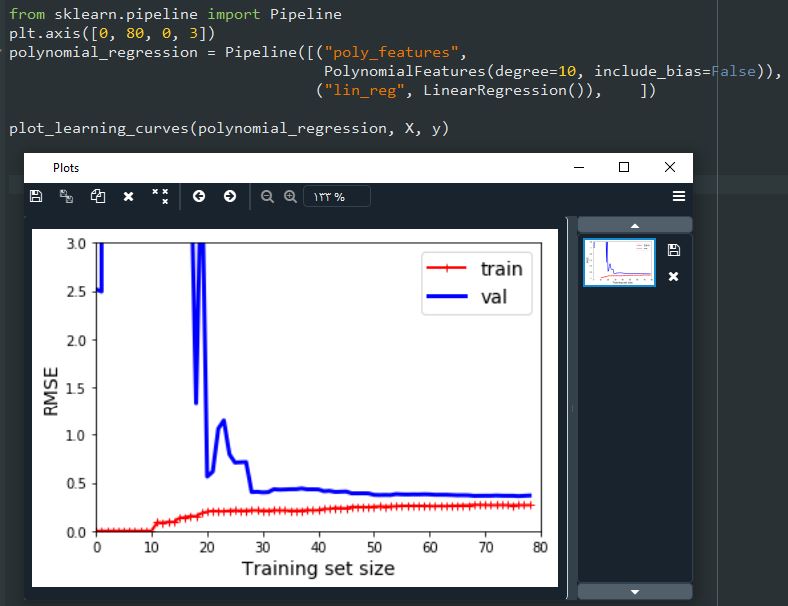
این منحنی هم کمی شبیه به قبلی هست اما تفاوت هایی داره:

• مقدار خطا روی ترینینگ ست خیلی کمتر از Linear Regression هست
• فاصله خیلی زیادی بین منحنی ها هست. این یعنی مدل فقط عملکرد خوبی روی ترینینگ دیتا داره که نشون دهنده اورفیتینگ هست. اگر از ترینینگ ست بزرگتری استفاده میکردیم، فاصله بین دو نمودار کمتر میشد.

یک راه برای افزایش عملکرد یک مدل اورفیت شده، افزایش ترینینگ دیتا تا جایی هست که مقدار دو خطا نزدیک هم بشن

مبادله سوگیری و واریانس

خطا های یک مدل جمع سه نوع خطای مختلف هست:

سوگیری (Bias)

این قسمت از خطا ها بخاطر اشتباه در فرضیات هست؛ مثلا فرض اینکه داده ها خطی هستند در حالی که درجه دو هستند. علت سوگیری زیاد یک مدل بخاطر آندرفیت بودن در ترینینگ ست هست.

واریانس (Variance)

این قسمت از خطا بخاطر حساسیت فوق‌العاده مدل به تغییرات کوچک در ترینینگ دیتا هست. یک مدل با درجه های آزادی زیاد (مثل Polynomial با درجه بالا) بیشتر در معرض داشتن واریانس بالا هست و واریانس بالا منجر به اورفیت شدن میشه.

خطای غیرقابل تقلیل (Irreducible Error)

این نوع خطا بخاطر نویز داشتن خود داده ها رخ میده. تنها راه برای کاهش این ارور تمیز کردن داده هاست ( مثلا مشکل منبع اطلاعات رو حل کنیم یا داده های پرت رو حذف کنیم)

افزایش پیچیدگی مدل معمولا منجر به افزایش واریانس و کاهش سوگیری میشه. از طرفی، کاهش پیچیدگی مدل منجر به کاهش واریانس و افزایش سوگیری میشه. به خاطر همین بهش میگن Bias Varience Trade-Off.

منظم سازی مدل های خطی

همونطور که در مطلب قبلی دیدیم، یک راه خوب برای کم کردن اورفیتینگ، Regularize کردن مدل هست (اعمال محدودیت). هرچقدر درجه آزادی کمتری داشته باشه، کمتر اورفیت میشه. یک راه ساده برای Regularize کردن مدل Polynomial، کم کردن درجه هاست.

برای یک مدل خطی، این عمل بصورت اعمال محدودیت در وزن های مدل انجام میشه. در ادامه مطلب درباره مدل های Ridge Regression، Lasso Regression و Elastic Net میخونید که سه راه مختلف برای محدود کردن وزن مدل هستن.

رگرسیون ستیغی

این رگرسیون Ridge Regression یا Tikhonov Regularization نام داره. این مقدار منظم سازی به تابع هزینه اضافه میشه. این مقدار، الگوریتم رو مجبور میکنه که نه تنها با داده ها تطابق پیدا کنه بلکه وزن های مدل رو تا جایی که امکان داره کوچیک نگه داره. دقت کنید که این مقدار باید در مرحله ترینینگ به تابع هزینه اضافه بشه. وقتی ترین مدل تموم شد، از معیار های ارزیابی عملکرد بدون این مقدار استفاده میکنیم. (استفاده از تابع های هزینه متفاوت در ترینینگ و تستینگ، کاملا رایج هست)

در فرمولی که دیدید، مقدار منظم سازی رو میشه با هایپرپارامتر آلفا مشخص کرد. اگر مقدار آلفا صفر باشه، درواقع داریم از رگرسیون خطی استفاده میکنیم. اگر آلفا خیلی بزرگ باشه، تمام وزن ها خیلی نزدیک به صفر میشن و نتیجه یک خط صاف خواهد بود که از میان میانگین داده ها عبور میکنه. تابع هزینه Ridge Regression رو میتونید ببینید:

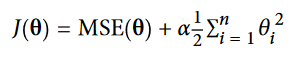
حتما قبل از استفاده از Ridge Regression باید مقیاس داده ها رو تغییر بدیم. این مدل هم مثل بیشتر مدل های منظم، به مقایس داده های ورودی حساس هست.

عکس زیر چند تا مدل Ridge رو نشون میده که با استفاده از یک سری داده خطی و مقادیر مختلف آلفا، ترین شدند. در سمت چپ، از مدل های ساده استفاده کردیم که منجر به خطی شدن تخمین ها شده. در سمت راست، اول داده ها با استفاده از PolynomialFeatures(degree=10) گسترده شدن، بعد با استفاده از StandardScaler مقیاس شون تغییر کرده و بعد از مدل Ridge استفاده شده. این یک Polynomial Regression با استفاده از Ridge Regularization هست. دقت کنید که چطور افزایش آلفا منجر به صاف شدن تخمین ها و در نهایت کم شدن واریانس و افزایش سوگیری شده.

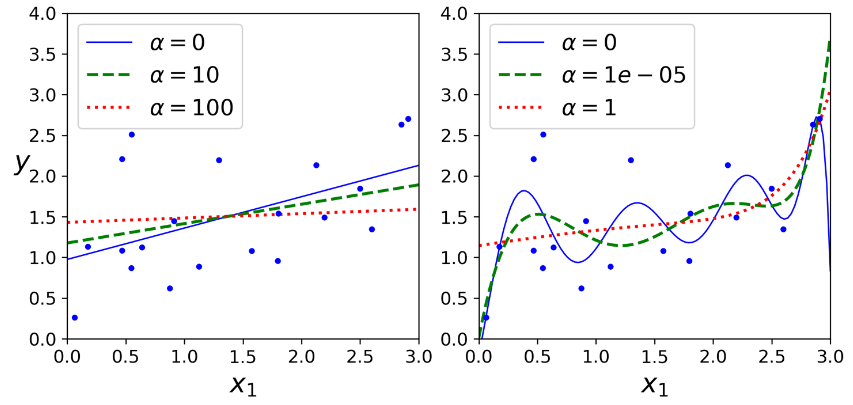
برای Linear Regression هم میتونیم با استفاده از معادله نرمال یا گرادیان کاهشی، از Ridge Regression استفاده کنیم. کد های زیر نحوه پیاده سازی رو نشون میده (مقدار penalty=l2 نشان دهنده Ridge Regression هست):

رگرسیون لسو

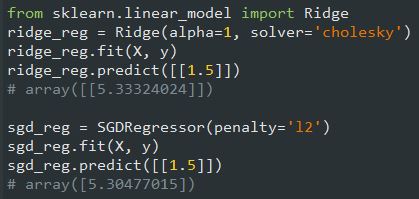
نام این مدل در واقع مخفف Least Absolute Shrinkage and Selection Operator Regression (LASSO) هست. این الگوریتم یک نوع دیگه از منظم سازی Linear Regression هست. مثل Ridge یک مقدار Regularization به تابع هزینه اضافه میکنه. فرمول رو میتونید ببینید:

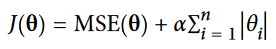
شکل زیر مثل شکل Ridge اما برای مدل Lasso هست.

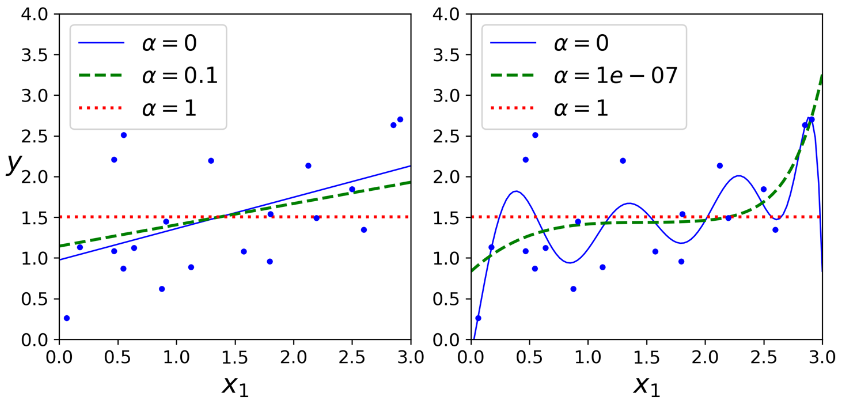
یک ویژگی مهم این الگوریتم این هست که وزن های فیچر های کم اهمیت رو حذف میکنه (برابر صفر قرار میده) به عبارت دیگه Lasso Regression به طور خودکار Feature Selection رو انجام میده.

با نگاه به شکل زیر میشه فهمید چرا این اتفاق میفته. محور های افقی و عمودی نشون دهنده پارامتر های دو مدل و پس زمینه نشون دهنده تابع های هزینه مختلف هست. نمودار گوشه بالا سمت چپ نشون دهنده L1 Loss (قدر مطلق تتا1 + قدر مطلق تتا2) هست که وقتی به هر کدوم از محور ها نزدیک میشیم، به صورت خطی کم میشه. مثلا اگر مقدار اولیه پارامتر های مدل رو برابر نقطه زرد قرار بدید و از گرادیان کاهشی استفاده کنید، هر دو پارامتر رو به مقدار مساوی کم میکنه (خط زرد) بخاطر همین تتا2 اول به صفر میرسه چون به صفر نزدیک تر هست. بعد از اون در طول محور حرکت میکنه تا زمانی که مقدار تتا1 هم برابر صفر بشه. نمودار بالا سمت راست نشون دهنده تابع هزینه Lasso هست. دایره های سفید نشون دهنده راهی هست که گرادیان کاهشی طی میکنه تا پارامتر هایی که مقدار اولیه تتا1 برابر 0.25 و تتا2 برابر -1 هست، بهینه کنه. دقت کنید باز هم راهی که طی کرده به سرعت به تتا2 مساوی 0 میرسه و بعد مدتی طول میکشه تا به حالت بهینه یعنی مربع قرمز برسه. اگر مقدار آلفا رو افزایش بدیم، حالت بهینه در طول خط زرد به سمت چپ و اگر کاهش بدیم، به سمت راست حرکت میکرد.

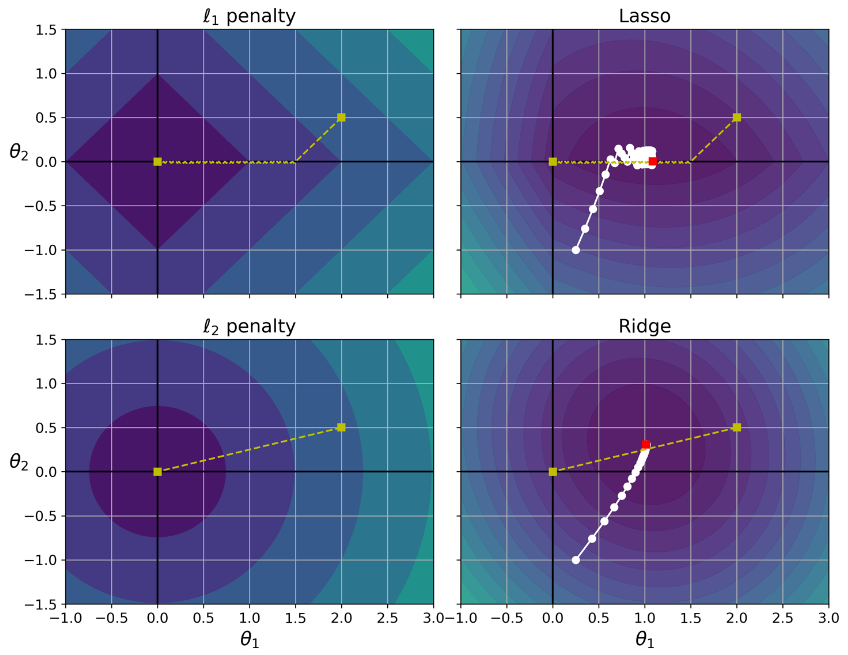
دو نمودار پایین همین موضوع رو با L2 Loss نشون میدن. نمودار پایین سمت چپ نشون میده که L2 Loss با نزدیک شدن به مبدا کاهش پیدا میکنه پس گرادیان کاهشی یک راه صاف رو برای رسیدن بهش طی خواهد کرد. نمودار Ridge دو تا فرق اساسی با Lasso داره. اول، مقدار گرادیان با نزدیک شدن به نقطه بهینه کمتر میشه پس گرادیان کاهشی به طور طبیعی آروم میشه و این قضیه به همگرایی کمک میکنه. دوم، نقطه بهینه که با قرمز مشخص شده با بیشتر شدن آلفا به مرکز نزدیک تر میشه.

در Lasso، برای جلوگیری از حرکت اضافه ی گرادیان کاهشی در اطراف نقطه بهینه، باید Learning Rate رو آروم آروم کم کنیم. با این کار باز هم حرکت اضافه خواهد داشت اما این بار با قدم های کوچکتر که منجر به همگرایی میشه

الگوریتم Elastic Net

این الگوریتم مابین Ridge و Lasso هست. در فرمولی که پایین میبینید، اگر r=0 باشه، به Ridge Regression و اگر r=1 باشه، به Lasso Regression میرسیم:

الان براتون سوال پیش میاد که کی باید از کدوم الگوریتم استفاده کنیم؟ خوبه که همیشه مقداری منظم سازی داشته باشیم، پس پیشنهاد میشه از Linear Regression خالی استفاده نکنید. بصورت دیفالت از Ridge استفاده کنید اما اگه شک دارید که فقط یک تعداد از فیچر ها به درد بخور هستند، از Lasso یا Elastic Net استفاده کنید چون این دو وزن فیچر های به درد نخور رو صفر میکنند. در حالت کلی، Elastic Net رو به Lasso ترجیح بدید چون اگر تعداد فیچر ها بیشتر از تعداد نمونه های ترینینگ باشه یا موقعی که بعضی فیچر ها به شدت همبسته باشن، Lasso نامنظم عمل میکنه.

توقف زودهنگام الگوریتم

یک راه کاملا متفاوت برای منظم سازی الگوریتم هایی مثل گرادیان کاهشی، متوقف کردن ترینینگ به محض رسیدن Validation Error به مینیمم هست. به این کار Early Stopping میگن. شکلی که میبینید یک مدل پیچیده رو نشون میده که با استفاده از BGD ترین شده. با افزایش Epoch مقدار ارور هم کاهش پیدا میکنه. اما از یک جایی به بعد، دیگه کم نمیشه و دوباره روند افزایش رو در پیش میگیره. با استفاده از Early Stopping میتونیم درست موقعی که به مقدار مینیمم ارور میرسیم، بایستیم.

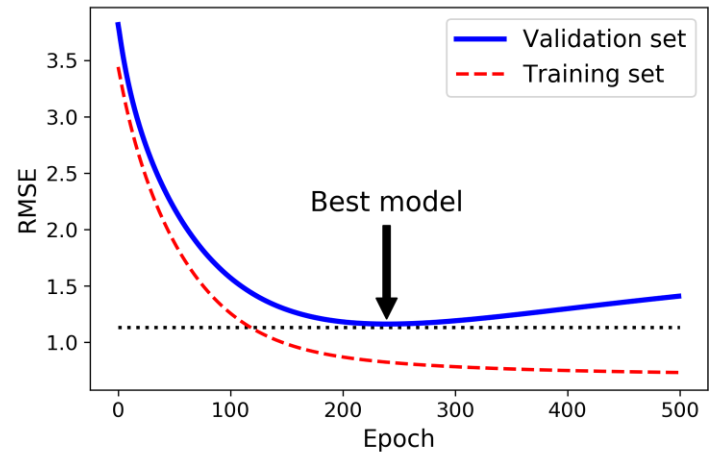
در الگوریتم های SGD و MbGD منحنی ها صاف نیستند و فهمیدن اینکه به مینیمم رسیدیم یا نه کار آسونی نیست. یک راه حل این هست اگه تا یک مدتی توی مینیمم بودیم، بایسیتیم (یعنی موقعی که مطمئن هستیم که عملکرد مدل دیگه قرار نیست بهتر از این بشه) بعد پارامتر های مدل رو به نقطه ای برگردونیم که ارور توی مینیمم بود

رگرسیون لجستیک

از بعضی الگوریتم های رگرسیون میشه برای دسته بندی استفاده کرد(و برعکس). Logistic Regression یک الگوریتم هست که احتمال متعلق بودن یک نمونه به یک دسته خاص رو تخمین میزنه. (مثلا چقدر احتمال داره که این ایمیل اسپم باشه؟) اگر احتمال تخمین زده شده بیشتر از 50% باشه، مدل نمونه رو جزء دسته مثبت و در غیر این صورت جزء دسته منفی میدونه. (کلاس مثبت با 1 و منفی با 0 لیبل گذاری شده) این قابلیت این الگوریتم رو به یک Binary Classifier تبدیل میکنه.

تخمین احتمالات

خب رگرسیون لجستیک چطور کار میکنه؟ این الگوریتم هم مثل رگرسیون خطی، مجموع وزن دار فیچر های ورودی رو به همراه یک مقدار خطا، محاسبه میکنه اما به جای اینکه مثل رگرسیون خطی، نتیجه نهایی رو نشون بده، شکل لجستیک نتیجه رو نشون میده.

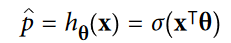
مدل لجستیک درواقع یک تابع سیگموئید (Sigmoid Function) که خروجی اون یک عدد بین 0 و 1 هست. نماد تابع سیگموئید رو به همراه شکل این تابع میتونید ببینید:

رگرسیون لجستیک بعد از تخمین احتمال، از این معادله استفاده میکنه تا نمونه رو دسته بندی کنه:

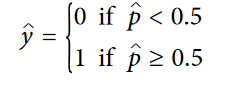
دقت کنید که به ازای t کوچکتر از صفر،مقدار تابع سیگموئید کوچکتر از 0.5 و اگر t بزرگتر یا مساوی صفر باشه، مقدار تابع بزرگ تر یا مساوی 0.5 خواهد بود.

مقدار t با نام logit هم شناخته میشه. ریشه این نام در تابع logit نهفته ست که معکوس تابع لجستیک هست. اگر p که احتمال رو نشون میده، به‌عنوان ورودی این تابع بدید، میبینید که نتیجه t خواهد بود. این تابع همچنین log-odds هم نام داره چون لگاریتم نسبت بین احتمال کلاس مثبت و احتمال کلاس منفی هست.

ترین و تابع هزینه

خب حالا میدونیم که یک مدل Logstic Regression چطور احتمالات رو محاسبه میکنه و حدس میزنه. اما چطور ترین میشه؟ هدف از ترین، مشخص کردن مقدار بردار تتا به گونه ای هست که احتمال نمونه های مثبت (y=1) و منفی (y=0) رو تخمین بزنه. این عمل برای هر نمونه بوسیله تابع هزینه زیر انجام میشه:

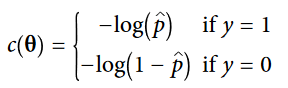
اگر t نزدیک به صفر باشه، log(t)- خیلی بزرگ میشه؛ در نتیجه هنگامی که مدل برای یک نمونه مثبت، احتمال نزدیک به صفر رو تخمین میزنه، و برای یک نمونه منفی، احتمال نزدیک به یک رو تخمین میزنه، مقدار هزینه خیلی زیاد میشه. از طرف دیگه، وقتی t نزدیک به 1 باشه، مقدار log(t)- نزدیک به 0 میشه. پس اگر احتمال یک نمونه منفی نزدیک به 0 و یک نمونه مثبت نزدیک به 1 باشه، مقدار هزینه هم نزدیک به 0 خواهد بود.

تابع هزینه برای کل ترینینگ ست، میانگین هزینه های تمام نمونه هاست. فرمول این تابع هزینه، Log Loss نام داره:

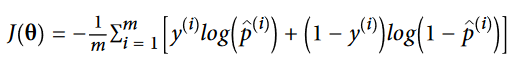
خبر بد اینه که برای محاسبه مقدار تتا، معادله نرمالی وجود نداره. خبر خوب اینه که این تابع هزینه محدب هست و میشه از گرادیان کاهشی(یا هر الگوریتم بهینه سازی دیگه ای) برای محاسبه مینیمم سراسری استفاده کرد. مشتق جزئی تابع هزینه به این صورت هست:

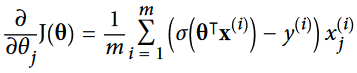
این فرمول برای هر نمونه مقدار خطای تخمین رو محاسبه میکنه و ضربدر مقدار j امین فیچر میکنه و بعد میانگین رو برای همه نمونه ها محاسبه میکنه. بعد از اینکه بردار گرادیان ها رو که شامل همه مقادیر مشتق جزئی هست، به دست آوردیم، میتونیم در BGD استفاده کنیم.همچنین برای SGD یک نمونه و برای MbGD یک دسته کوچک رو میگیریم.

مرز های تصمیم گیری

بیاید از دیتاست Iris برای شفاف سازی Logistic Regression استفاده کنیم. این دیتاست شامل طول و عرض کاسبرگ و گلبرگ 150 گل زنبق هست. این گلها از سه نوع مختلف به نام هایIris setosa، Iris versicolor Iris virginica تشکیل شدند.

بیاید برای تشخیص Iris virginica با استفاده از عرض گلبرگ، یک Classifier درست کنیم.اول داده ها رو دریافت میکنیم:

بعد مدل رو ترین میکنیم و نگاهی به احتمالاتی که تخمین زده میندازیم:

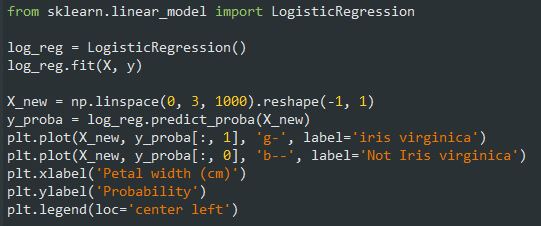
برای رسم از این کد استفاده میکنیم:

decision_boundary = X_new[y_proba[:, 1] >= 0.5][0]
plt.figure(figsize=(8, 3))
plt.plot(X[y==0], y[y==0], &quotbs&quot)
plt.plot(X[y==1], y[y==1], &quotg^&quot)
plt.plot([decision_boundary, decision_boundary], [-1, 2], &quotk:&quot, linewidth=2)
plt.plot(X_new, y_proba[:, 1], &quotg-&quot, linewidth=2, label=&quotIris virginica&quot)
plt.plot(X_new, y_proba[:, 0], &quotb--&quot, linewidth=2, label=&quotNot Iris virginica&quot)
plt.text(decision_boundary+0.02, 0.15, &quotDecision  boundary&quot, fontsize=14, color=&quotk&quot, ha=&quotcenter&quot)
plt.arrow(decision_boundary, 0.08, -0.3, 0, head_width=0.05, head_length=0.1, fc='b', ec='b')
plt.arrow(decision_boundary, 0.92, 0.3, 0, head_width=0.05, head_length=0.1, fc='g', ec='g')
plt.xlabel(&quotPetal width (cm)&quot, fontsize=14)
plt.ylabel(&quotProbability&quot, fontsize=14)
plt.legend(loc=&quotcenter left&quot, fontsize=14)
plt.axis([0, 3, -0.02, 1.02])

مثلث هایی که میبینید نشون دهنده عرض این نوع گل هست که از 1.4 تا 2.5 سانتی متر متغیره. مربع ها نشون دهنده عرض دیگر نوع های این گل هست که مقدار اونها 0.1 تا 1.8 سانتی متر هست. دقت کنید که بعضی جا ها این مقادیر هم‌پوشانی دارن. در بالای 2 سانتی متر، مدل مطمئن هست که گل از نوع Iris virginica هست (چون احتمالش بالا هست) در حالیکه در زیر 1 سانتی متر مطمئن هست که گل Iris virginica نیست. ما بین این مقادیر، مدل شک داره. اگر ازش بخواید که برای یک نمونه حدس بزنه (با استفاده از تابع predict) چیزی که برمیگردونه کلاسی هست که بیشترین احتمال رو داره. بخاطر همین یک مرز تصمیم گیری دور و بر 1.6 سانتی متر وجود داره چون اینجا هر دوی احتمال ها برابر 50% هست. اگر عرض بیشتر از 1.6 سانتی متر باشه نمونه جز دسته Iris virginica قرار میگیره و در غیر اینصورت، در دسته not Iris virginica.

شکل زیر دو تا فیچر این دیتاست رو نشون میده. رگرسیون لجستیک با استفاده از این دو فیچر، احتمال Iris virginica بودن یک نمونه رو تخمین میزنه. خط بریده بریده وسط نشون دهنده نقاطی هست که مدل احتمال 50% رو حدس میزنه: در واقع اینجا مرز تصمیمی گیری مدل هست. دقت کنید که این یک مرز خطی هست. هر خط نشون دهنده نقاطی هست که مدل یک احتمال خاص رو خروج میده؛ از 15% در سمت چپ تا 90% در سمت راست. تمام گل هایی که در بالا سمت راست خط قرار دارن، به احتمال 90% جزء دسته Iris virginica هستند.

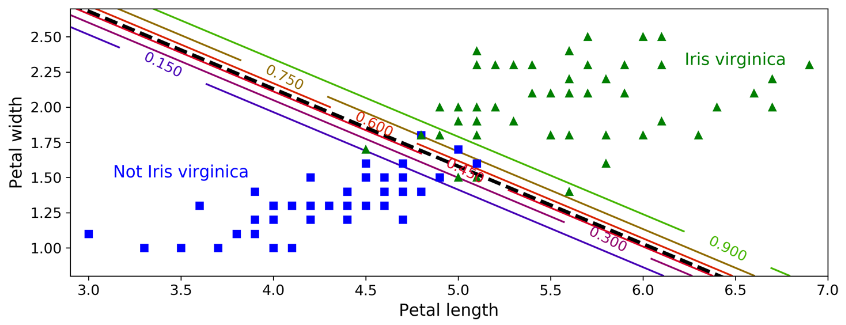
مثل بقیه مدل های خطی، رگرسیون لجستیک هم با استفاده از L1 و L2 میتونه منظم سازی بشه. Scikit-Learn به‌صورت دیفالت L2 رو پیاده سازی میکنه.

در مدل های خطی، هایپرپارامتر alpha وظیفه مشخص کردن میزان منظم سازی هست. اما در کلاس LogisticRegression ِ کتابخانه Scikit-Learn، هایپرپرامتر C این کار رو انجام میده. هر چقدر مقدار C بیشتر باشه، مدل کمتر منظم سازی میشه

رگرسیون سافت‌مکس

مدل رگرسیون لجستیک رو میشه عمومی‌سازی کرد تا بتونه به‌طور مستقیم چند کلاس رو دسته بندی کنه. این روش Softmax Regression یا Multinomial Logistic Regression نام داره.

ایده پشت این روش ساده‌ست: این مدل با دریافت یک نمونه، اول برای همه کلاس ها یک امتیاز رو محاسبه میکنه و بعد با دادن این امتیاز ها به تابع Softmax احتمال بودن در هر کلاس رو حدس میزنه. در فرمول زیر s نشون دهنده امتیاز هست و k نشون دهنده کلاس.

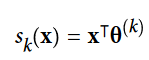
بعد از محاسبه امتیاز هر کلاس برای نمونه x ، میتونیم احتمال تعلق x به دسته k رو به دست بیاریم (Pk). این تابع اول exp همه امتیاز ها رو به دست میاره بعد با تقسیم این مقدار به جمع همه exp ها، اون رو نرمال میکنه.

رگرسیون سافت‌مکس میتونه یک کلاس رو حدس بزنه (multiclass هست نه multioutput). پس این الگوریتم رو فقط باید برای کلاس های متقابل منحصر به فرد استفاده بشه، مثلا انواع مختلف گیاهان. برای تشخیص افراد متعدد در یک عکس از این الگوریتم استفاده نمیکنیم

حالا که فهمیدیم مدل چجوری احتمالات رو تخمین میزنه و حدس انجام میده، بیاید یک نگاهی به روند ترین بندازیم. هدف، داشتن یک مدل هست که احتمال زیادی رو برای دسته هدف محاسبه میکنه (و احتمال کمی رو برای کلاس های دیگه). این کار رو میشه با به حداقل رسوندن مقدار تابع هزینه ای که در زیر میبینید، انجام داد. این فرمول Cross Entropy نام داره و هر وقت مدل یک احتمال کم برای کلاس هدف محاسبه میکنه، جریمه میشه.

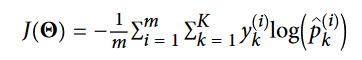
دقت کنید که اگر 2 تا کلاس داشته باشیم (K=2)، این تابع هزینه برابر با تابع هزینه رگرسیون لجستیک میشه.

بردار گرادیان این تابع هم به شکل زیر هست:

حالا میتونیم بردار گرادیان رو برای هر کلاس محاسبه کنیم و از گرادیان کاهشی (یا هر الگوریتم بهینه سازی دیگه) برای پیدا کردن پارامتری که مقدار تابع هزیه رو مینیمم میکنه، استفاده کنیم.

بیاید از Softmax Regression برای دسته بندی گل ها به سه دسته مختلف استفاده کنیم. به صورت دیفالت، کلاس LogisticRegression از one-versus-the-rest استفاده میکنه اما با استفاده از هایپرپارامتر multi_class=multinomial میتونیم از Softmax استفاده کنیم.

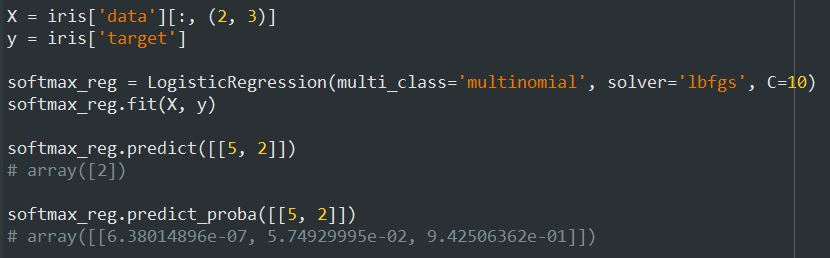
پس‌زمینه شکلی که میبینید، مرز های تصمیم گیری مختلف رو نشون میده. دقت کنید که مرز تصمیم گیری بین هر دو کلاس، خطی هست. همچنین احتمال کلاس Iris versicolor رو هم نشون میده (خطی که با 0.450 نامگذاری شده نشون دهنده مرز 45% هست) دقت کنید که مدل میتونه کلاسی رو که احتمالش زیر 50% هست، حدس بزنه. برای مثال، نقطه ای که همه مرز ها با هم برخورد کردند، احتمال همه کلاس ها برابر 33% هست.

خب این هم از بررسی مدل های رگرسیون خطی. امیدوارم مفید واقع شده باشه.