بررسی الگوریتم درخت تصمیم در ماشین لرنینگ

درست مثل الگوریتم‌های SVM، الگوریتم Decision Tree (درخت تصمیم) هم جزء الگوریتم‌های همه‌ کاره‌ی ماشین لرنینگ هست که از پس طبقه‌بندی، رگرسیون و حتی تسک‌های دارای چند خروجی برمیاد. این الگوریتم‌ها قدرت زیادی دارند و می‌تونند در دیتاست‌های پیچیده استفاده بشن. برای مثال، در مطلب قبلی یک DecisionTreeRegressor رو روی دیتاست خانه‌های کالیفرنیا پیاده‌سازی کردیم.

درخت تصمیم هم‌چنین جزء مولفه‌های اساسی الگوریتم Random Forest به‌حساب میاد. این الگوریتم هم جزء الگوریتم‌های قدرتمند ماشین لرنینگ هست.

در این مطلب می‌خوایم ببینیم چجوری درخت تصمیم رو ترین، مصورسازی و در نهایت برای حدس زدن آماده می‌کنند. سپس از الگوریتم CART استفاده می‌کنیم و می‌بینیم چطور درخت‌ها رو برای رگرسیون Regularize می‌کنن.

آموزش و مصورسازی یک درخت تصمیم

برای فهمیدن درخت‌های تصمیم، بیاید اول یکی بسازیم و ببینیم که چجوری حدس میزنه.

import numpy as np
import os
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)

# Where to save the figures
PROJECT_ROOT_DIR = &quot******&quot
CHAPTER_ID = &quotdecision_trees&quot
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, &quotimages&quot, CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
iris = load_iris()
X = iris.data[:, 2:] # petal length and width
y = iris.target
tree_clf = DecisionTreeClassifier(max_depth=2, random_state=42)
tree_clf.fit(X, y)

برای ترسیم این درخت تصمیم از graphviz استفاده می‌کنیم:

from graphviz import Source
from sklearn.tree import export_graphviz
        
export_graphviz(
        tree_clf,
        out_file=os.path.join(IMAGES_PATH, &quotiris_tree.dot&quot)
        feature_names=iris.feature_names[2:],
        class_names=iris.target_names,
        rounded=True,
        filled=True
)
g = Source.from_file(os.path.join(IMAGES_PATH, &quotiris_tree.dot&quot))
g.view()

حدس زدن

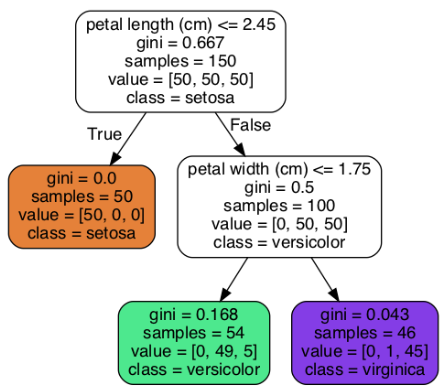
حالا ببینیم درختی که در تصویر بالا مشخص شده، چطور حدس میزنه. فرض کنید یک گل زنبق دارید و می‌خواید اون رو طبقه‌بندی کنید. از گره‌ی ریشه(Root Node) شروع می‌کنید (عمق صفر، واقع در بالای شکل): این گره می‌پرسه که آیا طول گلبرگ گل کوچک‌تر از 2.45 سانتی متر هست یا نه. اگر هست، به سمت گره‌ی فرزند واقع در سمت چپ حرکت می‌کنید (عمق یک، واقع در سمت چپ). با این شرایط، یک برگ به‌حساب میاد (یعنی گره‌ی فرزند نداره) پس هیچ سوالی نمیپرسه و حدسی که میزنه این هست که این گل یک Iris seosa هست (class = setosa)

حالا فرض کنید یک گل زنبق دیگه دارید و گلبرگ اون بزرگ‌تر از 2.45 سانتی متر هست. به گره‌ی فرزند واقع در سمت راست حرکت ‌می‌کنیم (عمق یک، واقع در سمت راست) چون این گره برگ نیست، پس باز هم سوال می‌پرسه: آیا عرض گلبرگ کوچک‌تر از 1.75 سانتی متر هست؟ اگر هست پس این گل یک Iris vesicolor هست (عمق 2 ، واقع در سمت چپ) اگر نیست، پس Iris virginica هست (عمق دو، واقع در سمت راست)

یکی از خوبی‌های درخت تصمیم این هست که برای استفاده از اون‌ها، آنچنان لازم نیست که داده‌ها رو آماده کنیم. در واقع، اصلا به تغییر مقیاس یا نرمال کردن احتیاج ندارن

در یک گره، sample تعداد نمونه‌های تمرینی که در اون گره هستند رو نشون میده. مثلا، 100 نمونه تمرین دارای گلبرگ با عرض بیشتر از 2.45 سانتی متر هستند (عمق 1، واقع در سمت راست) و از این بین، 54 نمونه عرض گلبرگ کوچک‌تر از 1.75 سانتی متر دارن (عمق 2، واقع در سمت چپ)

در یک گره، value تعداد نمونه‌های هر کلاس رو که در این گره هستند، نشون میده. برای مثال، گره‌ی پایین سمت راست دارای 0 نمونه از کلاس Iris setosa، یک نمونه از کلاس Iris versicolor و 45 نمونه از کلاس iris virginica هست.

در یک گره، gini مقدار impurity رو محاسبه می‌کنه (ناخالصی). یک گره pure (خالص) به‌حساب میاد(gini=0) اگر تمام نمونه‌های ترینینگ متعلق به یک کلاس باشند. مثلا گره‌ی سمت چپ با عمق 1 چون شامل تمام نمونه‌های iris setosa میشه، کاملا خالص هست و gini برابر 0 هست. معادله‌ی پایین مقدار Gini Impurity رو محاسبه می‌کنه.

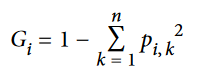
در این فرمول، p نشون دهنده نسبت نمونه‌های کلاس k در میان نمونه‌های گره‌ی i ام هست.

کتابخانه Scikit-Learn از الگوریتم CART استفاده می‌کنه. این الگوریتم فقط درخت‌های باینری تولید می‌کنه: گره‌های غیر برگ همیشه دو فرزند دارن ( یعنی همیشه جواب سوال‌ها بله/خیر هست) اگرچه دیگر الگوریتم‌ها مثل ID3 می‌تونن درخت‌های تصمیم با گره‌های بیش از دو فرزند تولید کنند

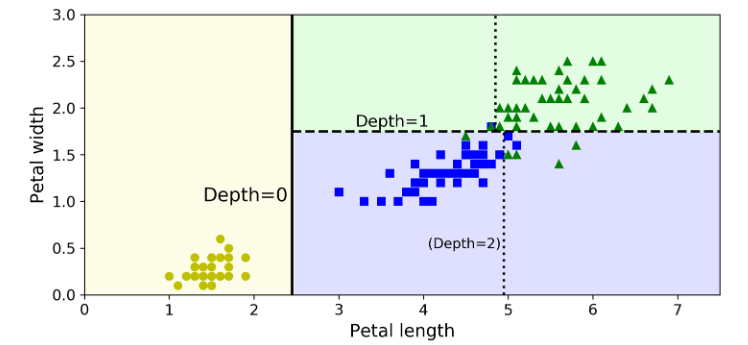
شکل زیر مرزهای تصمیم‌گیری درخت تصمیم رو نشون میده.خط عمودی زخیم نشون دهنده مرز تصمیم گره‌ی ریشه واقع در عمق صفر هست: طول گلبرگ برابر 2.45 سانتی متر. از اونجایی که قسمت سمت چپ خالص هست (فقط شامل نمونه‌های iris setosa هست)، بیشتر از این نمیشه اون رو جدا کرد. اما قسمت سمت راست ناخالصی داره در نتیجه عمق 1 در عرض گلبرگ برابر 1.75 سانتی متر جدا میشه (با خط بریده بریده نشون داده شده). از اونجایی که خودمون max_depth رو برابر 2 قرار دادیم، درخت تصمیم همینجا متوقف میشه. اگر اون رو برابر 3 قرار می‌دادیم یک مرز تصمیم دیگه هم اضافه می‌شد (با خط نقطه نقطه نشون داده شده)

تفسیر مدل: جعبه سیاه در برابر جعبه سفید

درخت های تصمیم شهودی هستند و نتیجه‌ای هم که میدن به راحتی قابل تفسیر هست. این مدل ها معروف به مدل های جعبه سفید هستند. در برابر اون‌ها، مدل های Random Forest و Neural Netwrok هستند که به مدل های جعبه سیاه معروف هستند. این مدل‌ها حدس‌های خوبی می‌زنند و می‌تونید محاسباتی هم که برای این حدس انجام شده ببینید؛ اما با این وجود معمولاً سخته که بشه توضیح داد چرا این حدس انجام شده. برای مثال، اگر یک شبکه عصبی بگه که یک شخص خاص در این تصویر حضور داره، سخته که بشه فهمید چه چیزی منجر به این حدس شده: آیا مدل چشم‌های شخص رو شناخت؟ یا دهن؟ یا دماغ؟ یا حتی مبلی که این شخص روش نشسته؟ اما در مقابل، درخت های تصمیم قوانین طبقه بندی ساده و خوبی دارند که حتی به صورت دستی هم میشه اون‌ها رو پیاده سازی کرد.

تخمین احتمالات کلاس

درخت تصمیم می‌تونه احتمال تعلق یک نمونه به کلاس k رو تخمین بزنه. در ابتدا از مسیر های درخت عبور میکنه تا گره‌ی برگ رو برای یک نمونه پیدا کنه و بعد نسبت نمونه‌های کلاس k رو در این برگ برمیگردونه. برای مثال، فرض کنید گلی داریم با طول گلبرگ 5 و عرض 1.5 سانتی متر. گره‌ی متناظر اون گره‌ی واقع در سمت چپ عمق 2 هست پس درخت تصمیم این احتمال‌ها رو بعنوان خروجی میده: 0% برای Iris setosa (0/54) 90.7% برای iris versicolor (49/54) و 9.3% برای Iris virginica(5/54). اگر ازش بخوایم که کلاس رو حدس بزنه، باید کلاس 1 یعنی Iris versicolor رو برگردونه چون بیشترین احتمال رو داره:

tree_clf.predict_proba([[5, 1.5]])
# array([[0.        , 0.90740741, 0.09259259]])
tree_clf.predict([[5, 1.5]])
# array([1])

الگوریتم CART

کتابخانه Scikit-Learn از الگوریتم Classification and Regression Tree برای ترین Decision Tree استفاده می‌کنه. روش کار این الگوریتم به این صورت هست که اول ترینینگ ست رو با استفاده از یک فیچر k و یک مرز tk (مثلا طول گلبرگ کوچکتر از 2.45 سانتی متر) به دو زیر مجموعه تقسیم می‌کنه. حالا چطور k و tk رو انتخاب می‌کنه؟ در واقع به دنبال جفت (k, tk) ای می‌گرده که خالص ترین زیرمجموعه رو تولید می‌کنه. معادله‌ی زیر تابع هزینه‌ی این الگوریتم رو نشون میده.

وقتی الگوریتم CART با موفقیت ترینینگ ست رو به دو قسمت تبدیل کرد، با همین منطق دوباره این زیرمجموعه‌ها رو تقسیم می‌کنه و به‌همین صورت بازگشتی ادامه پیدا می‌کنه. در دو صورت متوقف میشه: وقتی که به بیشترین عمق برسه (این عمق توسط هایپرپارامتر max_depth مشخص میشه) یا وقتی که دیگه نتونه تقسیمی رو پیدا کنه که ناخالصی رو کاهش میده. هایپرپارامتر های دیگه‌ای هم هستند که در ادامه صحبت می‌کنیم.

همونطور که می‌بینید الگوریتم CART یک الگوریتم حریصانه هست: به‌طور حریصانه برای یک تقسیم مطلوب جستجو می‌کنه و این روند رو در هر مرحله تکرار می‌کنه. این الگوریتم بررسی نمیکنه که آیا این تقسیم در مراحل پایین تر منجر به ناخالصی کمتر میشه یا نه. یک الگوریتم حریصانه معمولاً یک راه‌حل خوب ارائه میده اما تضمینی نیست که این راه حل ایده‌آل باشه.

متاسفانه، پیدا کردن درخت ایده‌آل جزء مسائل NP هست: به زمان O(exp(m)) برای حل شدن احتیاج داره که باعث میشه حتی برای ترینینگ ست های کوچیک هم غیر قابل کنترل بشه. بخاطر همین هست که همیشه باید به یک راه حل خوب قانع باشیم.

پیچیدگی محاسباتی

برای حدس زدن لازمه که از کل مسیر‌های درخت عبور کنیم و از ریشه به برگ برسیم. درخت تصمیم معمولاً به خوبی بهینه شده در نتیجه طی کردن مسیرهای درخت به O(log(m)) ریشه احتیاج داره(لگاریتم در مبنای 2 هست). چون هر ریشه باید مقدار یک فیچر رو بررسی کنه، پیچیدگی حدس برابر همین مقدار هست و مستقل از تعداد فیچرهاست. پس حدس زدن سریع هست و حتی با بزرگ‌تر شدن اندازه ترینینگ ست، باز هم به این صورت باقی میمونه.

الگوریتم در مرحله‌ی ترینینگ، تمام فیچر هارو برای هر نمونه در هر ریشه، مقایسه میکنه (یا اگر مقدار max_features تعیین شده باشه به همون اندازه چک می‌کنه). مقایسه کردن تمام فیچرها روی تمام نمونه‌ها در هر ریشه، پیچیدگی‌ای برابر O(n * m * log(m)) داره (لگاریتم در مبنای 2 هست) برای ترینینگ ست‌های کوچیک(کمتر از 1000 نمونه)، Scikit-Learn عمل ترین رو با مرتب‌سازی داده‌ها، سریع‌تر میکنه (presort=True) اما انجام این کار برای ترینینگ ست‌های بزرگ مارو با کاهش سرعت روبرو می‌کنه.

آنتروپی یا ناخالصی جینی؟

به‌صورت دیفالت، از ناخالصی جینی استفاده میشه اما می‌تونید از معیار ناخالصی آنتروپی هم استفاده کنید. برای این کار هایپرپارامتر criterion رو برابر entropy قرار می‌دیم. مفهوم آنتروپی از ترمودینامیک گرفته شده و معیاری برای بی‌نظمی مولکول‌هاست: اگر مولکول‌ها ساکن باشند و به‌خوبی نظم داشته باشند، آنتروپی نزدیک صفر خواهد بود. مفهوم آنتروپی بعدها در زمینه‌های دیگه‌ای هم استفاده شد مثل تئوری اطلاعات Shannon که میانگین محتوای اطلاعاتی یک پیام رو اندازه‌گیری میکنه. در اینجا اگر تمام پیغام‌ها یکسان باشند، آنتروپی برابر صفر هست.

در ماشین لرنینگ، آنتروپی معیاری برای محاسبه‌ی ناخالصیه: وقتی یک مجموعه فقط شامل نمونه‌های یک کلاس باشه، آنتروپی اون مجموعه برابر صفر هست. فرمول زیر نشون دهنده آنتروپی iامین ریشه هست.

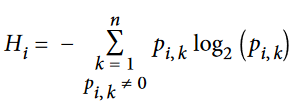
خب حالا باید از ناخالصی جینی استفاده کنیم یا آنتروپی؟ واقعیت اینه که بیشتر اوقات تفاوت خاصی بینشون نیست و مارو به یک درخت یکسان میرسونن. محاسبه ناخالصی جینی سریع‌تر هست و درنتیجه دیفالت از این استفاده می‌کنیم. اما در جاهایی که متفاوت هستند،ناخالصی جینی کلاسی که بیشترین تکرار رو داره، در شاخه‌ی درخت خودش ایزوله میکنه در حالیکه آنتروپی درخت‌های متعادل‌تری تولید میکنه.

هایپرپارامترهای منظم‌سازی

درخت تصمیم فرض‌های کمی درباره ترینینگ ست داره (بر خلاف مدل‌های خطی که فرض می‌کنن داده‌ها خطی هستند) اگر درخت تصمیم رو منظم‌سازی نکنیم، ساختار درخت خودش رو با ترینینگ ست وفق میده و خودش رو خیلی خوب با داده‌ها منطبق می‌کنه؛ درواقع دچار اورفیت میشه. به همچین مدلی میگن nonparamteric model (مدل غیر پارامتری). این به این معنی نیست که هیچ پارامتری نداره (اتفاقا پارامترهای زیادی داره) بلکه به این معنی هست که پارامترها قبل از آموزش تعیین نشدند در نتیجه ساختار مدل آزاد هست که خودش رو تا جایی که می‌تونه به داده‌ها نزدیک کنه. در طرف مقابل، paramteric model (مدل پارامتری)، مثل مدل خطی، تعدادی پارامتر از پیش تعیین شده داره، در نتیجه درجه‌ی آزادی اون محدود شده. در نتیجه احتمال اورفیت شدنش کاهش میابه (اما احتمال آندرفیت شدن رو افزایش میده)

برای جلوگیری از اورفیت شدن، باید در مرحله‌ی ترین آزادی درخت تصمیم رو محدود کنید. همونطور که می‌دونید، به این کار میگن Regularization. هایپرپارامترهای Regularization بستگی به الگوریتم دارن اما عموماً می‌تونید حداکثر عمق الگوریتم رو تعیین کنید. در Scikit-Learn این کار رو با استفاده از max_depth انجام میدیم. مقدار دیفالت این هایپرپارامتر None هست. کم‌کردن max_depth مدل رو Regularize میکنه و احتمال اورفیت شدن رو کم می‌کنه.

کلاس DecisionTreeClassifer تعدادی هایپرپارامتر برای محدود کردن شکل درخت تصمیم داره:

یک ) min_samples_split: حداقل تعداد نمونه‌هایی که یک گره باید داشته باشه تا تقسیم بشه

دو ) min_samples_leaf: حداقل تعداد نمونه‌هایی که یک گره‌ی برگ باید داشته باشه تا تقسیم بشه

سه ) min_weight_fraction_leaf: همون بالایی اما به‌صورت کسری از تعداد کل نمونه های وزنی بیان شده

چهار ) max_leaf_nodes: حداکثر تعداد گره‌های برگ

پنج ) max_features: حداکثر تعداد فیچرها که برای تقسیم در هر گره ارزیابی می شوند

در حالت کلی، کم کردن هایپرپارامترهای min_* یا max_* مدل رو Regularize میکنه.

بقیه الگوریتم‌ها اول درخت تصمیم رو ترین میکنن بعد ریشه‌های غیرضروری رو هرس (حذف) میکنن. یک ریشه که فرزندهای اون همگی گره‌ی برگ باشن غیرضروری به‌حساب میاد اگر افزایش بهبود خلوص از نظر آماری قابل توجیه نباشه. تست‌های استاندارد آماری مثل Che-Squarred Test برای تخمین احتمال اینکه بهبود خالصی صرفا نتیجه شانس بوده، استفاده میشه. (که بهش میگن Null Hypothesis) اگر این احتمال که بهش میگن p-value ،بیشتر از یک محدوده ای باشه ( معمولا 5%، که توسط یک هایپرپارامتر کنترل میشه) اونوقت اون ریشه غیرضروری محسوب میشه و فرزندان اون حذف میشن. این هرس تا جایی ادامه پیدا می‌کنه که تمام ریشه‌های غیرضروری حذف شده باشند.

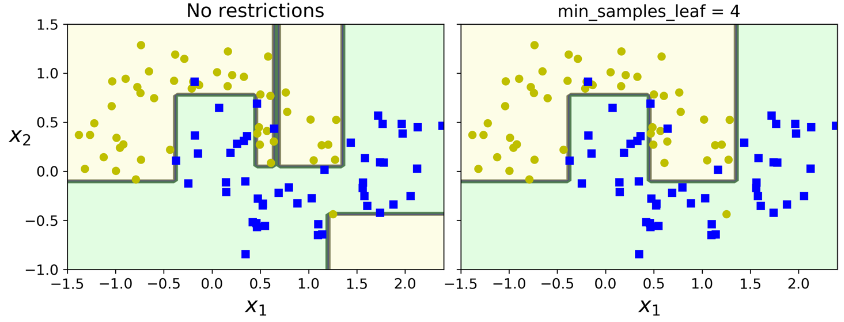
تصویر زیر دو درخت تصمیم رو نشون میده که روی دیتاست moon ترین شده. در سمت چپ مدل با هایپرپارامترهای دیفالت درست شده (بدون Regularization) و در سمت راست با استفاده از min_samples_leaf=4. مشخصه که مدل سمت چپ اورفیت شده و مدل سمت راست بهتر عمومی‌سازی می‌کنه.

رگرسیون

درخت تصمیم همچنین می‌تونه عملیات مربوط به رگرسیون رو هم انجام بده. بیاید از کلاس DecisionTreeRegressor استفاده کنیم:

from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor(max+depth=2)
tree_reg.fit(X, y)

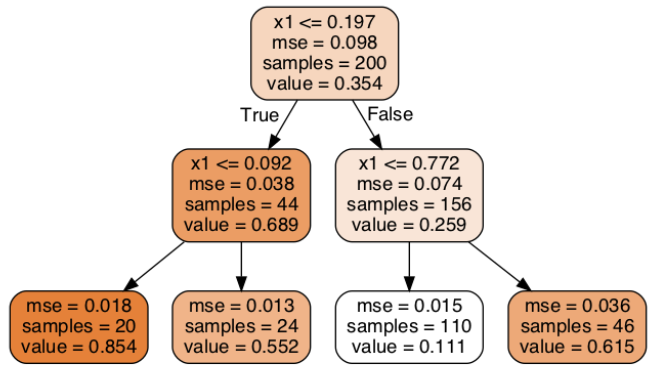
این درخت شبیه درختی هست که برای طبقه‌بندی درست کردیم. اصلی‌ترین تفاوت در این هست که به‌جای اینکه در هر ریشه یک کلاس حدس بزنه، یک مقدار حدس میزنه. برای مثال، فرض کنید می‌خوایم یک حدس برای نمونه‌ای با x1=0.6 انجام بدیم. از ریشه‌ی درخت شروع می‌کنیم و در نهایت مقدار value=0.111 رو حدس می‌زنیم. این مقدار در واقع میانگین مقادیر حدس زده شده برای 110 نمونه ترینینگ هست که توی این ریشه‌ی برگ وجود دارند و نتیجه‌ی اون mean squarred error برابر 0.015 هست.

حدس‌هایی که مدل زده در شکل مشخص شدند. اگر max_depth=3 باشه، شکل سمت راست نسیب‌تون میشه. دقت کنید که مقدار حدس زده شده برای هر منطقه همیشه برابر میانگین مقادیر حدس زده شده‌ی نمونه‌های اون منطقه هست. الگوریتم هر منطقه رو جوری بخش بندی میکنه که بیشتر نمونه‌های آموزش رو تا حد ممکن به مقدار پیش بینی شده نزدیک کنه.

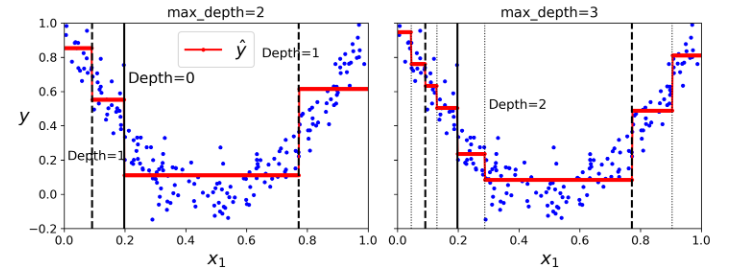
الگوریتم CART به‌جای اینکه بیاد ترینینگ ست رو طوری تقسیم کنه که ناخالصی رو کاهش بده، تلاش می‌کنه که ترینینگ ست رو طوری تقسیم کنه که MSE کاهش پیدا کنه. تابع هزینه رو می‌تونید ببینید:

مثل طبقه‌بندی، درخت تصمیم به‌هنگام رگرسیون هم در خطر اورفیت شدن هست. بدون Regularization (یعنی استفاده از هایپرپارامترهای دیفالت) حدس‌هامون شکل سمت چپ میشه. خب مشخصه که اورفیت شده. با تعیین min_samples_leaf=10 به مدل بهتری می‌رسیم یعنی شکل سمت راست.

بی‌ثباتی (Instability)

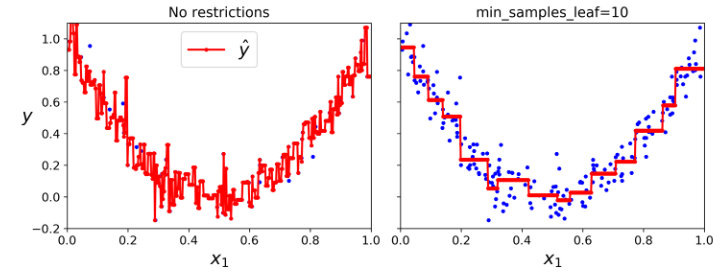
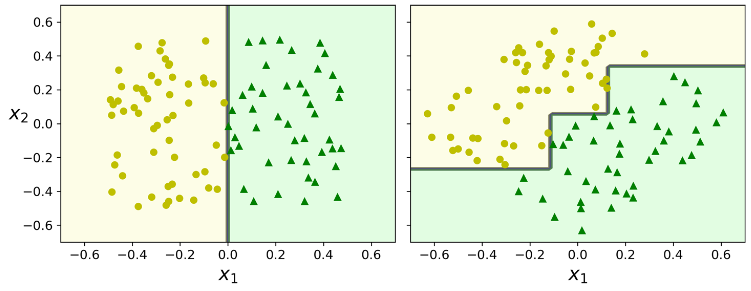
تا الان متقاعد شدید که درخت تصمیم خوبی‌های زیادی داره: فهمیدن و پیاده‌سازی راحتی داره، راحت میشه استفاده کرد و قدرتمند و وسیع هست. اگرچه، محدودیت‌هایی هم دارند. اول، همونطور که متوجه شدید، درخت تصمیم مرزهای تصمیم‌گیری قائم رو خیلی دوست داره (تمام تقسیم‌بندی ها عمود بر محورها هستند) این باعث میشه که به چرخش دیتاست حساس باشند. برای مثال شکل زیر رو در نظر بگیرید. این دیتاست رو به راحتی میشه با خط جدا کرد. در شکل سمت چپ درخت تصمیم به راحتی این کار رو انجام داده اما در شکل سمت راست که داده‌ها رو 45درجه چرخوندیم، مرز تصمیم‌گیری بی‌جهت پیچیده میشه. اگرچه که هر دو مرز تصمیم‌گیری به‌خوبی با داده‌ها تطابق پیدا می‌کنند اما احتمالا مدل سمت راست به‌خوبی عمومی‌سازی نکنه. یک راه برای حل این مشکل استفاده از Principal Component Analysis هست که باعث میشه ترینینگ ست در یک جهت مناسب قرار بگیره. در مطالب بعدی در این مورد صحبت خواهیم کرد.

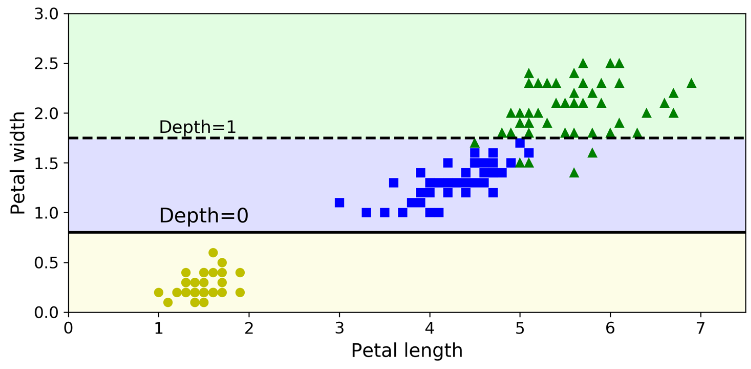
به طور کلی، اصلی ترین مشکل درخت تصمیم اینه که خیلی به تغییرات و دگرگونی‌های داخل داده‌های ترینینگ حساس هستند. برای مثال، اگر عریض‌ترین Iris versicolor رو از ترینینگ ست حذف کنیم (اون‌هایی که طول 4.8سانتی‌متر و عرض 1.8سانتی‌متر دارن) مدل شکل پایین حاصل میشه. همونطور که می‌بینید این مدل خیلی با مدلی که اول ارائه دادیم فرق داره. در واقع چون الگوریتیمی که Scikit-Learn استفاده میکنه Stochastic هست (در هر ریشه به‌صورت رندوم مجموعه‌ای از فیچرها رو انتخاب می‌کنه تا ارزیابی کنه) بخاطر همین روی دیتاست یکسان، به همچین مدل متفاوتی میرسیم. (مگر اینکه random_state رو تعیین کنید)

الگوریتم Random Forests می‌تونه این بی‌ثباتی رو با محاسبه میانگین حدس‌ها در درخت‌های متعدد، برطرف کنه. در مطالب بعدی به این الگوریتم می‌پردازیم.

این هم از الگوریتم Decision Tree. امیدوارم مفید واقع شده باشه.